The primordial aim of this paper is to address the issue on the development of a single, universalized equation to describe all wave functions of quantum systems in motion. That is, the idea of being able to explain their all of their possible evolutions related to the possible routes that these could potentially follow. As such, we will start off by analyzing a particular case of quantum wave interference, which is based on the notion of two probability waves –generated by a superposition of possible paths-that interact with each other due to a Mach-Zehnderlike interferometer. Although this certainly seems like a very particular experience, as this paper develops, we will see how it can be generalized in order to explain a vast number of phenomena. The importance and transcendence of the content found below hence relies on the idea that it provides an alternative method to evaluate quantum evolutions when wave functions interferences are implied. Overall, this is aimed at being a contribution that enrichens and polishes our understanding of the area, and that facilitates the process of tedious calculations related to these matters.

The primordial aim of this paper is to address the issue on the development of a single, universalized equation to describe all wave functions of quantum systems in motion. That is, the idea of being able to explain their all of their possible evolutions related to the possible routes that these could potentially follow. As such, we will start off by analyzing a particular case of quantum wave interference, which is based on the notion of two probability waves –generated by a superposition of possible paths-that interact with each other due to a Mach-Zehnderlike interferometer. Although this certainly seems like a very particular experience, as this paper develops, we will see how it can be generalized in order to explain a vast number of phenomena. The importance and transcendence of the content found below hence relies on the idea that it provides an alternative method to evaluate quantum evolutions when wave functions interferences are implied. Overall, this is aimed at being a contribution that enrichens and polishes our understanding of the area, and that facilitates the process of tedious calculations related to these matters.

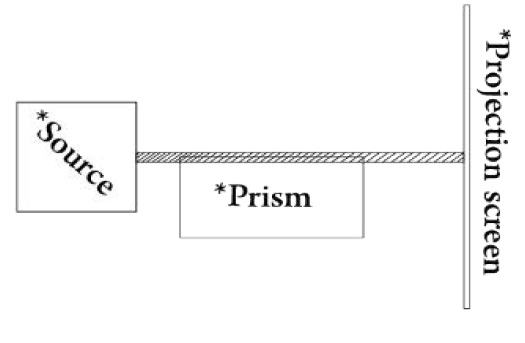
Imagine the following scenario: A regular laser, a prism and a projection screen have been placed and lined up over a table. The position of the laser has been arranged in such way that the path described by the light it emits is divided into two equal parts once it reaches the prism: one of them passes through the prism and the other one continues its regular route through the air. What we would see projected on the screen would be an interference pattern. As we know, this is a projection formed after two or more waves interact or interfere. Generically speaking, it looks like a large, horizontal strip made up of several, smaller vertical strips.

Interference patterns can be the result of many different arrangements, but they can all be reduced to the simple idea of waves interacting and, later on, crashing with a barrier called projection screen. In the comparatively large world we live in, only a much reduced number of physical systems can have a wave-like behavior. Liquids and some fluids like water, for example, have surfaces where waves can be easily formed; however, these systems are not behaving as waves by themselves: Only their most outer layers are doing so. Classical light, on the other hand, does behave like a wave in a considerable number of cases. It is for that reason, intuitively, that we mentioned previously that it had the capacity to generate interference patterns.

In the smallest scales possible, nevertheless, this idea of a reduced number of wave-like behaviors becomes radically different. Once we have reached the domain of quantum mechanics, what we see is that particles start behaving like waves. Although this certainly counterintuitive idea, it becomes the very essence of nature in the quantum world.

In this paper, for instance, what we are going to do become evident at this point: We will translate the first experience that I mentioned into a quantum scale and describe it using the laws of quantum physics. The underlying idea behind all this is very simple: The laser that we initially had will become-hypothetically and in our mental experiment-an individual source of photons on a much smaller scale.

Once we have managed to perform this translation and deduced laws from the previously proposed scenario, we will generalize these conditions and universalize these laws. After we have achieved this goal, it will become evident that our initial supposition can be used in order to describe a vast number of quantum phenomena.

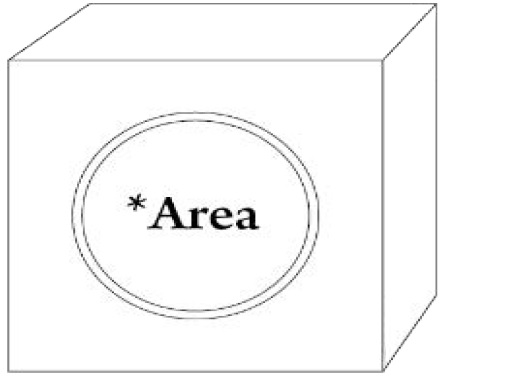
As it has just been mentioned, our first assumption is that the laser that was mentioned has become an individual source of photons. In principle, this-added to the change of scales-is all that it takes to quantize our initial experience. Now, the source must have an area from which photons are emitted. If we try to portray this notion, we would possibly get an apparatus similar to this one (Figure 1).

Evidently, this means that any photon emitted from that device could come from any point contained within the circular area. Now, let’s make another supposition: This area is directed to a prism, and the apparatus is placed in such a way that the projection of half of the area passes through the prism and the other one through the external mean. If we placed a detector in the point where the individual photons can take either possible route, we would measure that there is a 50-50 chance that the emitted photon will pass through the mean or through the prism. Holistically, so far, our experiment can be visualized with the following image (Figure 2).

However, assuming that there was not a way to detect which path they took, the individual photons would find themselves in a superposition of two possible states regarding the routes they could potentially take: thought the prism or through the mean. Overall, we would have two waves of possibility that would be out of phase, as the fact that one of them is a different mean implies that it has reduced its speed.

As a result, we would get an interference pattern. If we took into account the classical version of this experience, the resultant pattern would look approximately like this.

It is important to notice two things regarding Figure 3. First of all, it is a very general approximation of what is truly seen in the experience. Secondly, it is clear that the quantum and classical worlds are different, although the experience remains unchanged in principle (our hypothetical experiment is nothing but the quantum analogy of the classical experience). As such, Figure 3 is not a perfect approximation of what would be measured in a quantum domain.

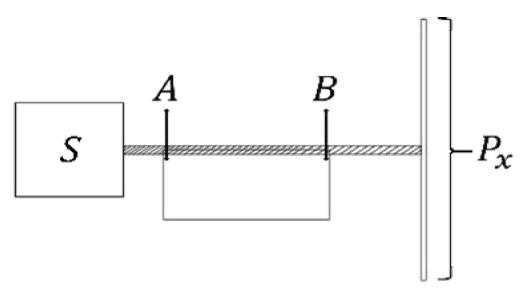
In order to generalize laws regarding our experience, it is imperative to, first of all, create an initial set of laws and equations. To do this, we will first create a graph and denote the points that will, later on, allow us to take the first step in our attempt to translate the experiment into a mathematical language. Figure 4 illustrates perfectly the notation that we will be using in this case.

From the graph, we can describe the sum of the routes taken by an individual photon that goes from the source to an undetermined point contained within the projection screen P_x. This algebraic description is given by

$${\langle P_x\text{|}S\rangle }_T={\langle P_x\text{|}S\rangle }_1+{\langle P_x\text{|}S\rangle }_2\left(1\right)$$

Where

$${\langle P_x\text{|}S\rangle }_1=\langle P_x\text{|}P\text{|}B\rangle \langle B\text{|}P\text{|}A\rangle \langle A\text{|}P\text{|}S\rangle \left(2\right)$$

And

$${\langle P_x\text{|}S\rangle }_2=\langle P_x\text{|}P\text{|}B\rangle \langle B\text{|}Q\text{|}A\rangle \langle A\text{|}P\text{|}S\rangle \left(3\right)$$

There is, however, a problem with this form of the equation: If we aim to operate numeric values that enable us to calculate the probability that the analyzed system has of landing at x P , we need an equation written in the language of complex numbers. This problem can be easily resolved if we assume the following (Table 1).

Table 1: Solution for language of complex number.

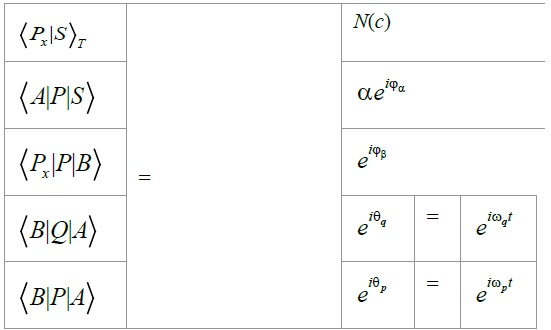
If we took this for granted, equation 1 would be equal to

$$N{\left(c\right)}_1=\alpha e^{i({\theta }_q+{\phi }_{\alpha }+{\phi }_{\beta })}+\alpha e^{i({\theta }_p+{\phi }_{\alpha }+{\phi }_{\beta })}\left(4\right)$$

Finally, if we normalize equation 4, we get that

$${|N_1|}^2=2{|\alpha |}^2(1+\cos \chi ) \left(5\right)$$

As α is nothing but the norm a of complex number, we can also write

$${|N_1|}^2=2{|C_1|}^2(1+\cos \chi )\left(6\right)$$

Where

$$\chi =\omega t_q-\omega t_{p }\left(7\right)$$

C₁= αβ (8)

and ${|N|}^2$ is the probability of a photon landing in a point x contained within the projection screen.

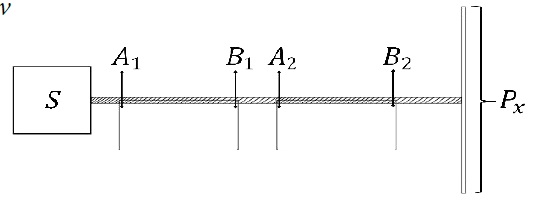
If we intend to generalize our experience, the first thing that we have to do is to introduce a slight variation on it. Because of convenience-related issues, this change will be an additional prism. Keep in mind that, for the sake of our analysis, we will assume that the prisms involved are not identical. If we applied the same logic used on 1.1, our diagram would look like this (Figure 5).

This would define the following, possible routes:

$${\langle P_x\text{|}S\rangle }_1=\langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}Q\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}Q\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle \left(9\right)$$

$${\langle P_x\text{|}S\rangle }_2=\langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}P\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}P\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle \left(10\right)$$

$${\langle P_x\text{|}S\rangle }_3=\langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}Q\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}P\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle \left(11\right)$$

and

$${\langle P_x\text{|}S\rangle }_4=\langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}P\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}Q\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle \left(12\right)$$

Overall, the combination of these equations would be given by

$${\langle P_x\text{|}S\rangle }_T={\displaystyle \sum }_{n=1}^4{\langle P_x\text{|}S\rangle }_n\left(13\right)$$

which is the same as writing:

$$\begin{array}{l}{\langle P_x\text{|}S\rangle }_T=\langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}Q\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}Q\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle +\\ \langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}P\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}P\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle +\left(14\right)\\ \langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}Q\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}P\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle +\\ \langle P_x\text{|}P\text{|}{B}_2\rangle \langle B_2\text{|}P\text{|}{A}_2\rangle \langle A_2\text{|}P\text{|}{B}_1\rangle \langle B_1\text{|}Q\text{|}{A}_1\rangle \langle A_1\text{|}P\text{|}S\rangle \end{array}$$

Again, we have to translate this new equation into a numerical notation. In order to do this, we will take for granted Table 2.

Table 2: Numerical notation.

With this in mind, we can write the new equation

$$N{\left(c\right)}_2=\alpha \beta e^{i(\epsilon +{\theta }_{q2}+{\theta }_{q1})}\alpha \beta e^{i(\epsilon +{\theta }_{p2}+{\theta }_{p1})}+\alpha \beta e^{i(\epsilon +{\theta }_{q2}+{\theta }_{p1})}+\alpha \beta e^{i(\epsilon +{\theta }_{p2}+{\theta }_{q1})}\left(15\right)$$

After normalizing equation 15, we get that

$${|N_2|}^2=2{|C_2|}^2\left(2+\cos {\chi }_1+\cos {\chi }_2+\cos {\chi }_3+\cos {\chi }_4+\cos {\chi }_5+\cos {\chi }_6\right)\text{}\left(16\right)$$

which is the same as

$${|N_2|}^2=2{|C_2|}^2\left( 2+{\displaystyle \sum }_{n=1}^6\cos {\chi }_n\right)\left(17\right)$$

The values at equations 16 & 17 are defined by the Table 3.

Table 3: Normalizing equations.

After analyzing the previous cases, it becomes evident that the vast majority of the terms implied in the equations depends on the number of prisms that are used. Overall, what we see is that, for a quantity of prisms, the following relation regarding the morphology of the resultant, normalized equation takes place:

$${|N_y|}^2=2{\left|C_y\right|}^2\left(2^{y-1}+{\displaystyle \sum }_{n=1}^{C_2^{2^y}}\cos {\chi }_n\right)\left(18\right)$$

In this equation, N is the norm of a complex number, whereas C_y is a real number and the product of Z complex numbers’ norms. It is important to take into account that

Z=y (19)

If the reader performs the procedure that resulted in equation 18, it will become evident that solving

$$C_2^{2^y}-\frac{2^y!}{2!(2^y-2)!}-isthesameas$$

Exp 1: $2^{y-1}(2^y-1)$

For instance, in a case where we have five prisms, the solution of equation 18 would be given by

$${|N_5|}^2=2{\left|C_5\right|}^2\left(2^{5-1}+{\displaystyle \sum }_{n=1}^{C_2^{2^5}}\cos {\chi }_n\right)\left(20\right)$$

which is the same as

$${|N_5|}^2=2{\left|C_5\right|}^2\left(16+{\displaystyle \sum }_{n=1}^{496}\cos {\chi }_n\right)\left(21\right)$$

Notice that equation 18 can also be used in the cases where there are not any prisms at all, as the solution for zero prisms would be

$${|N_0|}^2=2{\left|C_0\right|}^2\left(2^{0-1}+{\displaystyle \sum }_{n=1}^{C_2^{2^0}}\cos {\chi }_n\right)\left(22\right)$$

which would equal

$${|N_0|}^2=2{\left|C_0\right|}^2\left(\frac{1}{2}+\nexists \right)\left(23\right)$$

or

$${|N_0|}^2={\left|C_0\right|}^2\left(1\right)={\left|C_0\right|}^2\left(24\right)$$

Overall, this is, in principle, the same as the standard, normalized formula

$${\left|\varphi \text{|}\psi \right|}^2={\left|l_{C(\varphi )}\right|}^2\left(25\right)$$

where $l_{C(\varphi )}$ is the norm of the complex number associated with the state φ.

If solely the previously exposed generalization is used in order to simplify the resolution of a case with x prisms, some information regarding the value of the angles implied in cosines of the experiment will be lost. Because of this reason, now we will study a method that allows us to recover this information.

The first step is to draw the initial graph. Then, it is imperative to name the relevant points found within it, just as it was done at 1.1 and 1.2. Notice that it is essential to copy the cases found in section 1 (1.1 & 1.2) as diligently as possible.

Once the algebraic values have been defined, the next step is to add all the angles contained within each individual complex number, as in the examples shown below:

$$\epsilon +{\theta }_a+{\theta }_b+{\theta }_c={\text{Σ}}_1\left(26\right)$$

$$\epsilon +{\theta }_d+{\theta }_e+{\theta }_f={\text{Σ}}_2\left(27\right)$$

$$\epsilon +{\theta }_g+{\theta }_h+{\theta }_i={\text{Σ}}_3\left(28\right)$$

This will give us a set of groups of angles, each one of them denoted by ${\text{Σ}}_x$ , where x equals the number of the group. Notice that the total number of groups ( $n_{\text{Σ}}$ ) is defined by

$$n_{\text{Σ}}=2^y\left(29\right)$$

If $\epsilon$ is defined as the addition of the angles that are present in every complex number involved in the problem (in the case of 1.1, it would be equal to ${\phi }_{\alpha }+{\phi }_{\beta }$ ; on the other hand, at 1.2 it would be ( ${\phi }_{\alpha }+{\phi }_{\beta }+{\phi }_{\gamma }$ ), the number of remaining angles- $n_{\theta }$ -would be equivalent to

$$n_{\theta }=2y\left(30\right)$$

Assuming that we take these premises for granted, the recovery method becomes extremely simple: The first cosine’s angle will be the difference between the first group and the second one, the second angle related to a cosine will be the difference between the first group and the third one, etc. Once it is impossible to proceed by taking the first group as the first term in the subtraction, the second one will take its place.

Notice that, once we reach the point in which the first term in the subtraction is the second group, the subtractions are defined as the difference between the second group and the following ones. We do not take any previous group into account. This logic also applies to the next shifts regarding which group occupies the position of the first term in the subtraction.

For instance, in a case where there are two prisms, our methodology (once it has been finished) would look like this (Table 4).

Table 4: Methodology in two prisms.

Let’s take into account that, according to our resolution (Table 5).

Table 5: Final resolution.

If we take a look at the analysis at 2.1, it becomes evident that equation 18 is universal, in the sense that it can be applied to any amount of prisms and is even true when there are not any prisms at all. Now, it is important to remember the fact that we never truly defined the variables that we placed with an exact value. This freedom regarding the capacity to take any possible, defined value implies that our equations are not only applicable to prisms: They are applicable regardless of the mean that is used to generate the interference. It is just a matter of adjusting the precise values given to each variable of the equation.

As we mentioned previously, the equations that we have defined are also valid in cases where there aren’t any prisms. Subsequently, it is acceptable to say that they must apply to any case that aims to describe the route or possible routes taken by any quantum system. This is more properly described the probability that has a system $|\psi \rangle$ located at X_a of landing in an undetermined point X_b. If we take into account this notation, it would be more accurate to rewrite equation 18 like this:

$${|\psi (X_b)\text{|}\psi (X_a)|}^2=2{\left|C_y\right|}^2\left(2^{y-1}+{\displaystyle \sum }_{n=1}^{C_2^{2^y}}\cos {\chi }_n\right)\left(31\right)$$

In order to finalize this generalization, let’s consider the fact that, overall, every single quantum state can be described by a wave function, not only the ones linked to the idea of displacement. This means that, given that, under a methodical perspective, there is no principle difference between describing a state linked to position and any other one (say, linked to the spin of an electron), equation 31 could also be used to describe the evolution of any other state we desire to evaluate. In effect, the fact that we have been using prisms implies that we are also taking general evolutions into account, as these imply a change in the phase of wavelengths of systems. It all comes down to matter of changing the interpretation of our evaluation, in terms of the exposure to a certain evolution, from distance to time (e.g, the prisms exposed a system to an evolution for a distance x; now, the evolution will be defined by a time y, rather than a distance).

Notice that this does not mean that we have to change our equations, as all it entails to make them suited to these more general mental experiments is to define in the setting of the experiments the values of our terms as reliant on time. In way, this has already been done, though, that is why $e^{i\theta }=e^{i\omega t}$ . Holistically speaking, we now see that equation 31 is more accurate described as a the probability that has a system described by $|\psi \rangle$ of collapsing in a state $|\psi \text{'}\rangle$ . This would be written as:

$${|\langle \psi \text{'}\text{|}\psi \rangle |}^2=2{\left|C_y\right|}^2\left(2^{y-1}+{\displaystyle \sum }_{n=1}^{C_2^{2^y}}\cos {\chi }_n\right)\left(32\right)$$

Keep in mind that equation 32 is applicable and works if and only if the states of $|\psi \rangle$ and their corresponding evolution can be described as an interference between them that is prolonged through a mean (regardless of its nature) or throughout time.

Schrödinger’s equation establishes that the evolution of any quantum system $|\psi \rangle$ evaluated at a time t is given by

$$\stackrel{⌢}{H}|\psi (t)=i\hslash \frac{d}{dt}|\psi (t)\left(33\right)$$

Where $\stackrel{⌢}{H}$ is the matrix that represents the evolution of the system. As we can define all systems as the addition of all their possible states,

$$|\psi ={\displaystyle \sum }_{n=0}^{I-1}{a}_n|n-\left(34\right)$$

where I equal the number of possible states of the system and a_n is a complex number-, we can expand equation 33 in order to get

$$\stackrel{⌢}{H}|\psi (t)=i\hslash \frac{d}{dt}{\displaystyle \sum }_{n=0}^{I-1}{a}_n(t)|n\left(35\right)$$

With this in mind, we can create a set of equations that allows us to evaluate simultaneously the probability that has a system to land in a determined point of space and its Hamiltonian evolution using equations 32 & 35.

$${|\psi \text{'}\text{|}\psi |}^2=2{\left|C_y\right|}^2\left(2^{y-1}+{\displaystyle \sum }_{n=1}^{C_2^{2^y}}\cos {\chi }_n\right)$$

$$\stackrel{⌢}{H}|\psi (t)=i\hslash \frac{d}{dt}{\displaystyle \sum }_{n=0}^{I-1}{a}_n(t)|n$$

Set 1

The practicality of using this set relies on the fact that it allows the user to analyze in a parallel manner the probability that has a quantum system of landing at a specific point and what would be its evolution if it reached this point.

Moreover, the core difference between these two ways of analyzing quantum evolutions relies on grounds of practical convenience. When there is route a particle is to follow (implying thus multiple evolutions), it may be more convenient to opt for our generalization. However, when the base states of a system are left to evolve throughout a determined time span, it is more direct to apply Schrödinger’s equation.

Holistically speaking, it is possible to generalize the evolution of quantum systems in motion and bounded to a determined set of enacted operations via the equation

$${|\psi \text{'}\text{|}\psi |}^2=2{\left|C_y\right|}^2\left(2^{y-1}+{\displaystyle \sum }_{n=1}^{C_2^{2^y}}\cos {\chi }_n\right)$$

where y is the number of state-interference-inducing apparatuses.

This generalized formula is applicable as long as the evaluated quantum system is bounded to a displacement linked to a possible evolution due to an inference in the wave function describing its possible states involving a determined property [1-10].