Journal Name: Scholar Journal of Applied Sciences and Research
Article Type: Research
Received date: 18 June, 2018
Accepted date: 06 July, 2018
Published date: 18 July, 2018
Citation: Chaker A, Benaissa A, Zeblah A, Belafdal A (2018) Bat Algorithm Used for a Network Optimization. Sch J Appl Sci Res. Vol: 1, Issu: 4 (49 - 54).
Copyright: © 2018 Chaker A, et al . This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Optimization techniques tend towards new methods, these methods are based on the nature of the impact thereof on the lifestyle of human beings, engineers working on new optimization approaches to achieve the objective of maximizing reliability of the electric current and with the minimal cost which means that our structure of network must answer this requirement, a new approach proves to solve major problems using a heuristic méta- which is called algorithm of beater (BA).
Keywords
Bat algorithm (BA); Optimization; The design of the power system; Reliability; Universal moment generating function (UMGF).
Abstract
Optimization techniques tend towards new methods, these methods are based on the nature of the impact thereof on the lifestyle of human beings, engineers working on new optimization approaches to achieve the objective of maximizing reliability of the electric current and with the minimal cost which means that our structure of network must answer this requirement, a new approach proves to solve major problems using a heuristic méta- which is called algorithm of beater (BA).
Keywords
Bat algorithm (BA); Optimization; The design of the power system; Reliability; Universal moment generating function (UMGF).
Abbreviation
ci: Cost of electrical component I; Ai: Available of electrical components technologies; gi: Power components performance; ri: Power components reliability; ri: Power components reliability; ROP: Redundancy Optimization Problem; BA: Bat Algorithm; AC: Ant Colony Algorithm; GA: Genetic Algorithm; HS: Harmony Search Algorithm.
Introduction
The reliability of the system, depends on each electric components which constitutes the system, and must answer the latter, it is the reason for which the good performance of our system must reach this level, therefore to always reduce the investment costs of the elements of our structure which constitutes our system. However the problem in the design of structure of network is to obtain a hand to maximize reliability of the system and with the minimal investment prone to the constraints of the tolerance and the reliability and the total costs of the fuel system.
In our problem, the function objectifies which is, the reduction of the total costs and that under maximum influence of reliability for the only reason to build a structure of the reliable network defines that under certain constraint for the systems design of food. The whole of manufacturers know this problem well and tend to optimize the redundancy (safety device in the event of an imbalance of the system) [1-3]. Once the application of the reliability of all the systems is applied, one regards it as a measurable size for our design and must correspond has the satisfaction of the request namely by provide a sufficient quantity of electrical energy [4,5]. These problems and unambiguous of failure is because; according to the specifications proposed by the customer the rated capacity generators will be never defective.
The load diagram of the consumer and that of the system are taken into account of made that it intervenes in the process of the evaluation of reliability. Our system is composed of a structure based on components technologies for the design of our electric system, we consider another time the load diagram of the consumer it is taken into account because it enters the constitution of the reliability of the system as all the components are taken in consideration because it is a problem of optimization of the feeding system of energy. The same problem is quoted in [6], which was formulated to optimize the reference in the basic approach [4], the component costs are taken in consideration and the capacities which compose the system, and the application was considered using a curved load. The disadvantage of the approach inside [3] and [4] is that the cost of components is defined as analytical explicit according to their capacities and of the values of the index of reliability are assignees with all the type indicating of the components independently of their capacity. In [7-8], the different meta-heuristic ones used in it modest work for a comparison, genetic algorithm, colony of ant, harmony seeks and the algorithm of the bats are employed to solve problems of technical order of optimization. we propose one algorithm news which is the algorithm of the bats (BA) to provide the design a structure of the feeding system with a choice inexpensive and optimal of the suitable electric components which compose (of the generators, of transformers and of the electric lines of technology) product range available on the electric market of the components for each type of electric components. The true one encloses practical, it is that there exists a great diversification of choice of products is available, and each components is characterized by a technology that it is in performance, cost, and reliability. Our algorithm (BA) selects by simple combinations of the components to arrive at an optimization of system with a reduced cost, however, the production, transfers it and the routing of this production is to feed a whole networks with a condition quoted in top under constraint cost and with a performance also to book with one tolerance of so powerful reliability. For the evaluation of the reliability of the structure of the feeding system in our case in parallel series, the development of one démarche one develops the fast and effective method which is based on Function of universal production (WMU) [4,7-9].
Description and Problematic Formulation of the Structure of the Network
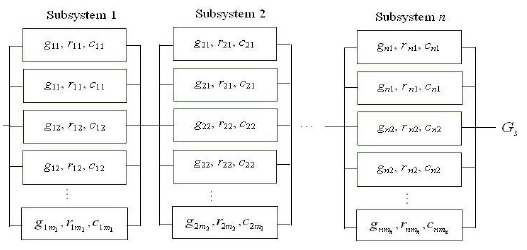
On (Figure 1) one presented the whole of the sub-system seriesparallel for “n” component which constitute it.
Figure 1: Series-parallel power system.
Our system requirements are composed for not distorted the equation of “n, m” electric components assembled in parallel series knowing that all elements of kind, moreover i=1, ..., n components of powers are selected of kind i in the structure of which there are a multiplicity of technologies who different ones with the others by quality that it is performance, cost and reliability and capacity. These elements are defines in our system by names chosen to answer the equation these indices are cim, rim, gim. The structure of our system parallel series is defined by a component vectorial ki={ kimi} (1 ≤ i ≤ n, 1 ≤ j ≤ mi) and the total costs of the system for the whole of the system are given k1, k2,……., kn by the equation which is written so below:
Electrical energy sudden continuously of the losses what leads us inevitably has a loss in the index of the probability of load (LOLP) and moreover the period T energy to deploy (EENS) in this function, are two great parameters which contribute has the estimate of reliability [5]. The calculation of the index of this probability allows us of carried out a load whose whole did not tighten not taken into account. The chart of the random curve discrete and often taken by the request of the load If the period of time of the load is the whole of M intervals, with the duration, dj and Tj each level of request Tj (j=1,….,M) has the duration, the LOLP is calculated as follows:
and
The expression of the probability P (gs ≤ d j) represent the probability of all the system and dj is equal to or higher than gs compared to the level of the request. All the productions and requires of capacities are defined like a calculation proportional of their total face value. The graph of the cumulative load diagram is determined by vectors d={di} and T={Ti} who is parameters determined for each element of the system. The calculation of reliability is carried out by the indexing of R in the reference [2], given by the expression R=1- LOLP. This indexing is compared to R0 and must be not less values inferior of the specific initial value.
The difficulty of the optimization of reliability of the system and the design of a network lies primarily in the choice of the elements which constitute the system which is perhaps formulated as follow k1, k2, ...,kn: what pushes us with find a design of system who certifies a cost in totality is minimal under constraint of reliability. This difficulty can be known is carried out like below:
Subject To: R(d,t,k1,k2,….,kn) ≥ R0
Description Assessment of Reliability
Our question quoted with by before is a question of optimization, it is essential of city several states possible of the system. It is the reason which he is obligatory employee a fast and effective procedure to consider reliability structural As mentioned previously, the major question is to estimate reliability R for the arbitrary continuations and the parallel circuit, and it is essential that the probability of all the structure of the electric system of refill is equal to a level of detail of the request for load, it will be calculated in the following way:
R(d )=P(g
This evaluation of reliability is based on modern methods and mathematical techniques as observed above: technique of UGF (or U-transform) in [10-12]. The latter was applied for the estimate and the optimization of the solidity of the power circuit in [13-14], and interprets an occurring prolongation of function one ordinary moment [15]. The UGF, in our case, of a discrete variable E is thus given polynomial:
where the discrete random variable g has J possible values and Pj is the probability that g is equal to gj. Under consideration if only the components with total failures are considered. For instance for each element of type i and technology m has reliability Rimi and nominal capacity gim, then we denote by:
P(g=gs)=Rim and P(g=0)=1-Rim. The UGF can be defined of such an element has only two terms as:
A brief overview on UGF method with respect to its applications for multi-states system (MSS) which has a finite number of states, there can be m different levels of output performance at each time t:g(t) ϵ g={gh ,1 ≤ j ≤ m} and the system output performance can be defined by two finite vectors g and p={ph (t)}=Pr{g(t)= gh} 1 ≤ h ≤ m, here the UGF, represented by the polynomial u(z) can define all the MSS output performance, i.e. it represent all the possible states of the system by relating the probability of each state to performance of MSS in that state in the form:
Having the MSS output performance, the system reliability for arbitrary time t and demand d can be obtained using the following operator ΩA.
In clearer, the probability that all the faculty of the circuit of refill is not less than one precise request of level of loading; it is possible to write it thus
P{g ≥ d}=(u(z)z-d)
where Ω is a distributive operator defined by the following expression:
and
For the installation of the feeding system containing of the components laid out of various manners, in parallel, all the capacity is equal to the sum of all the components of the capacity There with front, the U-function can be calculated using the Operator Ґ:
Where
We notice that the operator Ґ is with simplicity a polynomial production and representative u- function of the system in particular and containing m elements assembled in series. Another example if the circuit comprises attached components in a chain, mitigated operation is established by the worst condition observed for any of its components it is the reason why in employment another coefficient 𝛽 and which leads us to:
Us(z)=β {u1(z),…., um(z)}
whose value of 𝛽 is:
β (g1,….,gm)= min(g1,….,gm)
The MSS reliability was presented and P{g ≥ d} after time has passed for this probability becomes constant.
The Bat Optimization Approach
The bats are flying mammals, and which proceed of the wings, and they have also the ability to perceive sounds which emit one calls it “echolocation”. Whose most microchiroptères use this means which is echolocation for nourished because they are insectivorous, for protected from predatory and to locate to perch cracks in the dark darkness to them. It is estimated that there are approximately 1,000 various species of bat, which represents up to 20% of all the mammalian species. Their size varies the tiny ones bats bumblebee (from approximately 1.5 to 2 G) with the giant bats with a scale of approximately 2 m and weight going until approximately 1 kg. The microchiroptères generally have a front armlever length from approximately 2.2 to 11 cm.
These bats emit a very strong noise and to listen to the echo which rebounds starting from the surrounding objects. Their impulses vary in properties and can be in correlation with their strategies of hunting, according to the species. Most bats use, of short signals modulated in frequency to sweep approximately an octave, others generally use signals at constant frequency for echolocation. Their signal with band-width varies according to the species and increases by using often more harmonics.
Studies show that microchiroptères uses time delay of the emission and the detection of the echo, time difference between their two ears, and the variations of sound intensity of the echoes to build a scenario in three dimensions of surrounding or they are. They can detect the distance and the orientation from the target, the type of prey, and even the rate of travel of the prey, such as the small insects. Indeed, studies suggest that the bats seem to be able to distinguish the targets by the variations from the Doppler effect induced by the rates of the target insects wing undulation.
Algorithm (BA) beats is a method méta-heuristics based on an algorithm of optimization which was initially inspired by the life of the bats to find their food [16]. The bald people mouse emit signals has place or they are and of écoûté the echo of recalls this process known as of echolocation to locate itself by report has the prey. BA is mainly built by the use of four principal ideas [16]:
- Echolocation allows the bat of distinguished food the difference between the preys (prey and object).
- Each bat in position Xi steals at the speed of production of one Vi particular impulse with the frequency and the intensity of the fi and Ai respectively.
- The volume of Have exchange in various Ai ways such as the reduction of a great value to a low value.
- The frequency ri, fi and laughed of rate of each impulse is controlled automatically. Initially, all the bats fly randomly within the space of research producing of the random impulses. After each flight, the position of each bat is put up to date in the following way:
Where XG has the best overall solution. The limit of the upper frequency and the lower frequency sounds of the nth bat are represented by and . The population size is the total number of designated snowshoe NB,φ1 and is a number generated randomly between 0 and 1.
The second position of the movement of the bat is simulated as follows:
Epsilon “ϵ” is a random number in the beach of the segment [-1.1] and for the improvement of the amplitude for all the bald people mouse. Once the position of the bald people mouse is improved by the adjustments above and the new random individual is produced if it the level of signal is larger than a random value 𝛽.
One insert the new solution found by the new member in the population has condition which one observes the constraint:
[𝛽
As previously mentioned the value of the amplitudes of signal generated by the bats a progressive reduction formulated has by
Ainew=αAiold
Ґiltrer+1=Ґ[1-exp(-γ.t)]
Constants α and 𝛽 are the approachs important for the bald people mouse, and represent the iteration count in the algorithm
Step 1: Initialize the bat population or their position . Define pulse frequency fi at . Initialize pulse rates ri and the loudness A.
Step 2: Generate new solutions by adjusting frequency, and updating velocities and locations/solutions (Equation (10)).
Step 3: if (rand > ri ) Select a solution among the best solutions Generate a local solution around the selected best solution.
Step 4: Else generate a new solution by flying randomly.
Step 5: If ([𝛽
Step 6: Rank the bats and find the current best .
Step 7: While (iteration < Max number of iterations) Post process results and visualization. The algorithm stops with the total-best solution.
Power Design Example
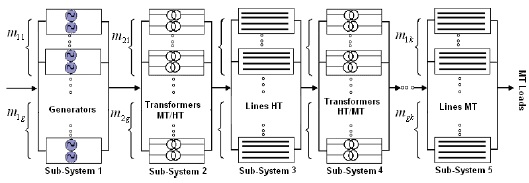
Table 1 summarizes the different technology components that will consevoir then our system vien Table 2 contains the cumulative power of the data request of the Year To illustrate the proposals of the Mete - heutistique that different bat BA algorithms, PSO, GA and HS for the construction and design of our system as shown in Figure 2, a numerical example is solved by the use of the data provided in Tables 3. Every electrical component of the subsystem is considered a unit with total failures.
Table 1: Data of available different power components technologies.
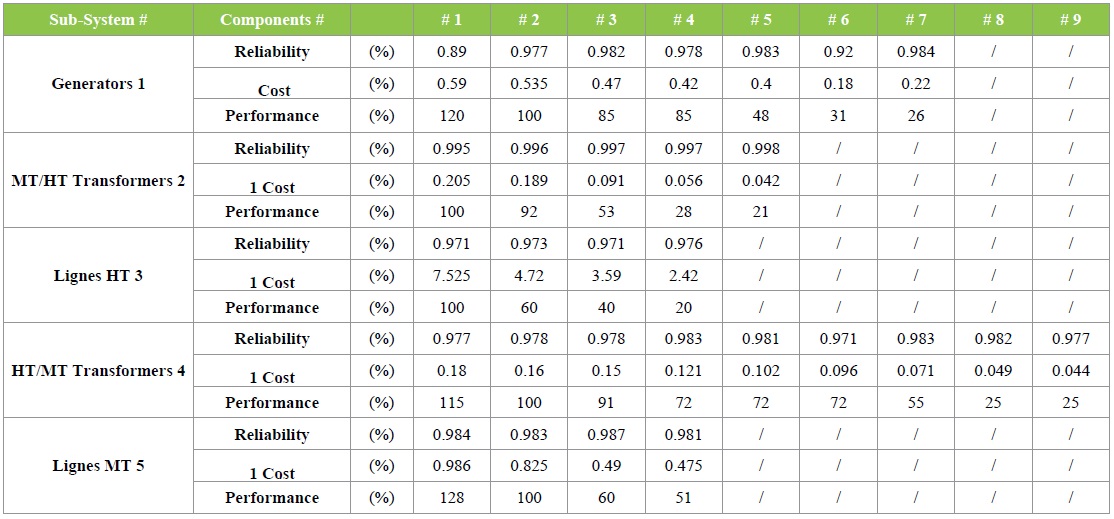
Table 2: Parameters of the power demand curve.

Table 3: Optimal solution obtained by different algorithms, bat, ant colony, harmony serch and genetic algorithm.
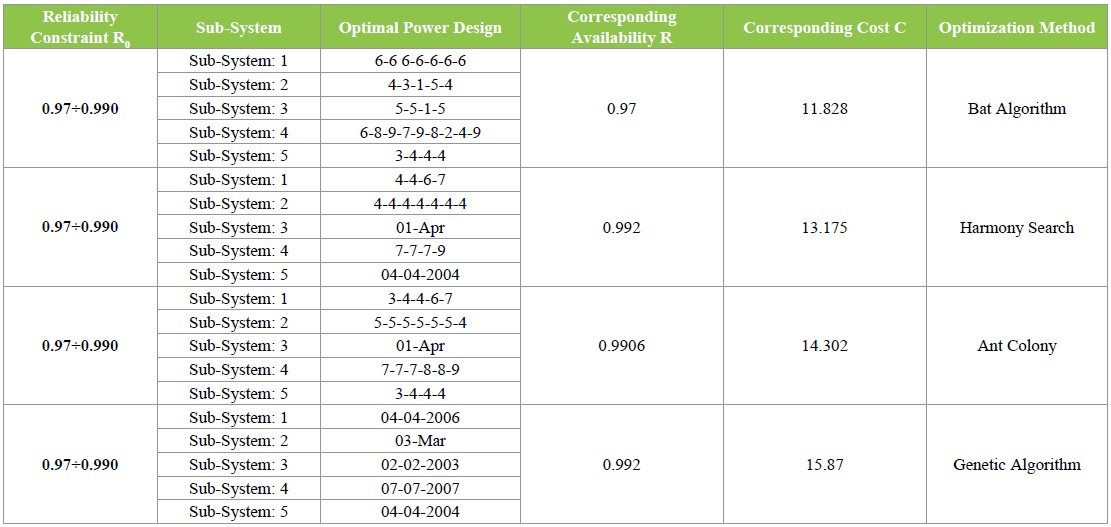
Figure 2: Series- parallel power design.
With a true simulation delivered by an example real of (G. Levitin) for each algorithm, knowing that the structure of the network is described with a number maximum gmax, for components which are placed parallel one take account of the values and of the parameters of this one the results are compared for all these metaheuristic we summarize in the Table 3 which represents different meta-heuristic thus the configuration from the networks for the design, with lower costs and better a reliability. Knowing that the data of the availability of different component technologies are listed in Tables 3.
Discussion for Results
The implementation of the bi-inspired bat algorithm to the series parallel heterogeneous system has proposed to determine the best configuration with the minimum investment cost.
The proposed problem is subject to the given high level of reliability taken as decision variable constraint. The goal optimization process was based on the combination of various variables decisions as (version of components and algorithm parameters). Also the universal moment generating to evaluate the corresponding constraint by verifying for each iteration the feasibility solution.
In Second part the above Table 3 shows the best optimal power design obtained by the suggested meta heuristic’s (Bat, harmony search, ant colony and genetic algorithms) for one desired reliability levels R0 (0.97-0.990). The illustrates the index of evaluation of the price and the availability to the corresponding development of energy. In algorithm beats a series characterized by data are tested. For several parameters of data of the algorithm corresponds to a design of system of power: Mass of the population=500; iteration number=500; loudness=0.02; and the pulse ratean=0.45. The diversification of the influential values forcing gave better results.
The comparison and all the more effective if one measures the coefficient of quality of the result by NN (Nakagawa and Nakachima) and that one takes only to the best result given by the algorithm and taken one consideration NN
The results shows that the NN coefficient of optimal design given by bat algorithm is (λ =11.82/0.97) is very low than HS, ACO and GA.
For the different meta-heuristic ones proposed for a comparison in this modest work which is beats it algorithm, the colonies of ants, the antigens and the harmonies seek (BA, ACO, GA and HS), allows us to conclude that BA after having to start the programme leads us to spectacular solution. If one compares with those found by different the méta heuristic used and an optimal design of the network of power gives us. The difference between these comparative méta-heuristics in the table shows us well that for a beach of reliability gives and its constraint and the cost and its constraint gives us good performance and of this made optimal solutions for the design of the network.
Conclusion
This modest work deals thanks to a new meta-heuristic solving the optimization of the design of an electrical system which is a very interesting question often posed in the energy industry. it is formulated as a problem of redundancy. This new meta-heuristic for solving this problem, however, is based on an algorithm bats our algorithm creates a design such that it is optimal cost and reliable for the system of electricity supply, our system is composed a model structure. this under certain stress algorithm allows us to have a minimum investment cost under constraints with maximum reliability under stress and the cost and reliability. So our algorithm we selected material from a list of products available in the market with technology components, and the list also includes the cost of these products so their performance, this also results in the definition of these components that we will introduce in each sub system with which it also sets the components of electrical power series-parallel to each subsystem when demand changed the consumers. All projects methods to solve part of the optimization problem namely the optimal design of networks (Cost and reliability) with a wide range of product components that make up these subsystems without limiting the various technologies electrical components in series.
- parallel.
- to it was put a new generation algorithm that could have some time given the best results compared to other algorithms it is the bat algorithms who is compared to algorithms (HS) , (ACO) and ( GA) for the same problem.
Liang YC, Smith AE (2001) An ant colony approach to redundancy allocation. IEEE Transaction on Reliability. [ Ref ]
Chowdhury BH and Rahman S (1990) A review of recent advances in economic dispatch. IEEE Trans Power Syst 5: 1248-1257. [ Ref ]
David W, Smith AE (1995) Optimization approaches to the redundancy allocation problem forseries-parallel systems. Proceeding of the fourth industrial engineering research conference (IERC). [ Ref ]
Ushakov IA (1987) Optimal standby problems and a universal generating function. Sov J Compt Syst Sci 25: 79-82. [ Ref ]
Billiton R, Allan R (1984) Reliability of power systems. Pitman, London. [ Ref ]
Ushakov IA and Harrison A (1994) Handbook of reliability engineering. Wiley and Sons, NY/Chichester/Toronto, USA. [ Ref ]
Nourelfath M, Nahas N, Zeblah A (2003) An ant colony approach to redundancy optimization for multi-state system. In: International Conference on industrial engineering and production management (IEPM’2003), Porto-Portugal. [ Ref ]
Massim Y, Zeblah A, Ghoraf A, Meziane R (2005) Reliability Evaluation Of Multi-State Series-Parallel Power System Under Multi- States Constraints. Electrical Engineering Journal, Springer Verlags 87: 327-336. [ Ref ]
Levitin G, Lisniaski A, Ben-haim H, Elmakis D (1996) Power system structure optimization subject to reliability constraints, Electric Power System research 39: 145-152. [ Ref ]
Su CT, Lin CT (2000) New approach with a Hopfield modeling framework to economic dispatch. IEEE Transactions on Power System 15: 541-545. [ Ref ]
Niknam T, Doagou Mojarrad H, Nayeripour M (2009) A new fuzzy adaptive particle swarm optimization for nonsmooth economic dispatch. Energy 35: 1764-1778. [ Ref ]
Walters DC, Sheble GB (1993) Genetic algorithm solution of economic dispatch with valve point loading. IEEE Trans Power Syst 8: 1325-1332. [ Ref ]
Chiang CL (2005) Improved genetic algorithm for power economic dispatch of units with valve-point effects and multiple fuels. IEEE Trans Power Syst 20: 1690-1699. [ Ref ]
Ongsakul W, Dechanupapritttha S, Ngamroo I (2004) Parallel tabu search algorithm for constrained economic dispatch. IEE Proc Gener Transm Distrib 151: 157-166. [ Ref ]
Wang KP, Fung CC (2006) Simulate annealing base economic dispatch algorithm. IEE Proc C 140: 507-513. [ Ref ]
Dodu JC, Martin P, Merlin A, Pouget J (1972) An optimal formulation and solution of short-range operating problems for a power system with flow constraints. IEEE Proc 60: 54-63. [ Ref ]