This paper deals with a new approach in the formation of periods in the Mendeleev’s Periodic Table. Using a newly suggested formula and newly suggested quantum states for the external electron shells of atoms of chemical elements, a reconfiguration of periods in the Mendeleev’s table has been put forward. It is assumed to reduce the number of periods in the table, which is proved by the material represented in the paper. The following order of formation of electron layers is suggested: the principle quantum number (n), followed by the quantum state of electrons (first and second) which constitute the electron configurations of subperiods, and only after that - the remaining quantum orbitals (s, d, f, and p).

The periodic table of the Mendeleev, Principle quantum numbers, Energy.

This paper deals with a new approach in the formation of periods in the Mendeleev’s Periodic Table. Using a newly suggested formula and newly suggested quantum states for the external electron shells of atoms of chemical elements, a reconfiguration of periods in the Mendeleev’s table has been put forward. It is assumed to reduce the number of periods in the table, which is proved by the material represented in the paper. The following order of formation of electron layers is suggested: the principle quantum number (n), followed by the quantum state of electrons (first and second) which constitute the electron configurations of subperiods, and only after that - the remaining quantum orbitals (s, d, f, and p).

The periodic table of the Mendeleev, Principle quantum numbers, Energy.

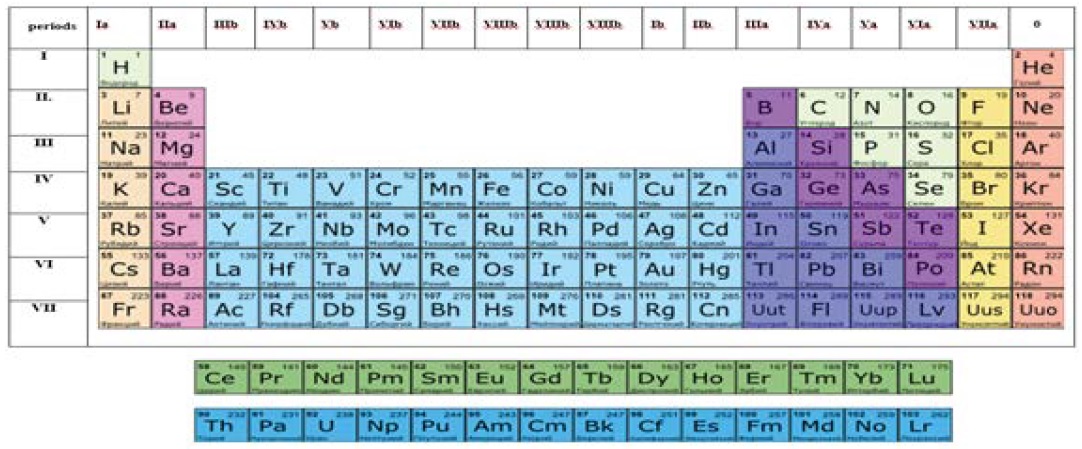
For almost 150 years up till now, chemical engineers of all the world have been using the periodic law discovered by D. I. Mendeleev and its graphic representation in the form of the Mendeleev’ Table [1,2]. After a substantial addition made a bit more than a hundred years ago stating that the periodicity in the distinction of chemical properties of elements does not depend on the mass but on the charge of their atomic nuclei, we have been using the periodic table so far almost without any essential changes in the substance and content. This is another emphasis upon its great significance for the chemical science all the more so as it is one of the few laws of science which has no full-fledged mathematical formulation. The periodic table is a visual aid which demonstrates the link between the electron structure of the atoms of chemical elements and the location of these elements in the table. It explains the specifics of chemical properties depending on the structure of electron shells of atoms. And it also proves the primary structure of these electron shells [3,4].

Table 1: Correlation between the number of chemical elements in periods with the number of electrons calculated with formula (I).

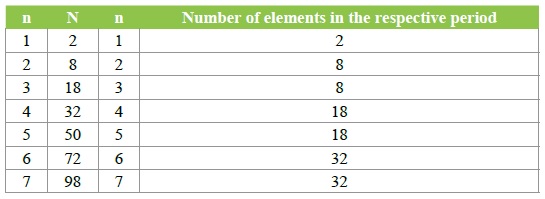
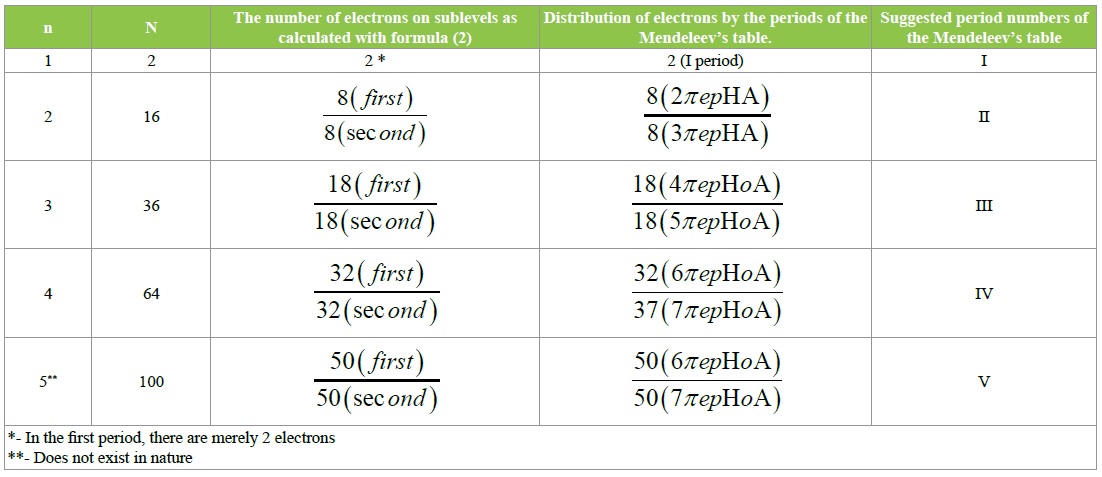
Table 2: Correlation of the number of electrons in periods, as was calculated with formula II, and concomitant findings.

At the same time, the Mendeleev’s Table adopted by us for practical use (Figures 1) has its specific contradictions which do not let show its potential to the full. For instance, the essential contradiction is the unconformity between the sequence of infilling specific series of orbitals of various chemical elements related to various n (principle quantum numbers, or energy levels).

This is vividly seen if we use the well-known formula N= 2n²…(I) to calculate the total number of electrons N related to the respective principle quantum number n. At the same time, as is known, the principle quantum number also denotes the number of respective period in the Mendeleev’s Table. Calculated amounts of electrons for various values of n are represented in (Table 1) where the data of correlation between n and the number of chemical elements in the periods of the Mendeleev’s table is also listed.

As can be seen from Table I, the total number of elements in most periods does not match the calculated number of electrons for the same period. The number of electrons becomes greater than the charge of the atomic nucleus of an element, but that is basically impossible by the electroneutrality of the atom of an element. Such a state of things makes it possible to deduce an inference that for great values of the principle quantum number and the atomic number of a period formula (I) at least does not work.

A contradiction also arises when examining the matter of sequence following which the electrons infill their electron orbitals. Specifically, 3d electrons of the third principle quantum number start in filling their orbitals only after 4s electrons of the fourth period, although logic suggests that they are related to a different energy level and their infill should probably occur earlier.

To elucidate and solve the above contradictions, we suggest carrying out the following analysis of the Mendeleev’s Periodic system. It is vividly seen from (Figure 1) and (Table 1) that there exists a certain sequence in the table. This sequence is that the periods 2 с 3; 4 с 5; 6 с 7 interduplicate the amounts of chemical elements contained in them. Such a recurrence in certain intervals allows to deduce an inference on the existence of common principles in the composition of electron shells of atoms of these respective periods. In the general case, such a recurrence was noted by the American chemist Lewis [5] who demonstrated that infill of electron shells with electrons is running in successive layers, following the general principles of composition of their electron configurations.

In the case of the Mendeleev’s Table, the key point, in our opinion, is that complete periods comprise 2, 8, 18, and 32 chemical elements each [6,7]. Therefore, the same quantity of electrons on the external electron shells should match them. It appears from this that in such case the energy states of these electron shells should differ substantially between one another, but only on condition the electron shells contain different quantities of electrons. In case the number of electrons on the electron shell is equal, we can assume that they relate to an energy level which is common for them thus forming sequential two layers (sublevels) but within the same principal quantum number which is the same for them. In other words, unlike the Mendeleev’s table, we assume the option of separation of respective energy levels into two sublevels. Since the principle quantum number corresponds to the period number in the Mendeleev’s table, counting the number of electrons on these sublevels was of a particular interest to us. We suggest performing such counting of electrons using the following new formula:

N= (2n)² (II)

Where,

Using equation (II), through division of N by 2 (the number of sublevels), it is easy to calculate the number of electrons at each of the sublevels.

We carried out calculations for various values of n, which yielded the following results represented in (Table 2). Table 2 demonstrates a distinct sequence in the structure of electron shells of the atoms of elements.

Specifically, two sublevels with the same numbers of electrons on them belong to each of the energy levels. But most important is that these sublevels sequentially, by the number of electrons on them, correspond to the periods of the Mendeleev’s table applied by us. That is also represented in (Table 2).

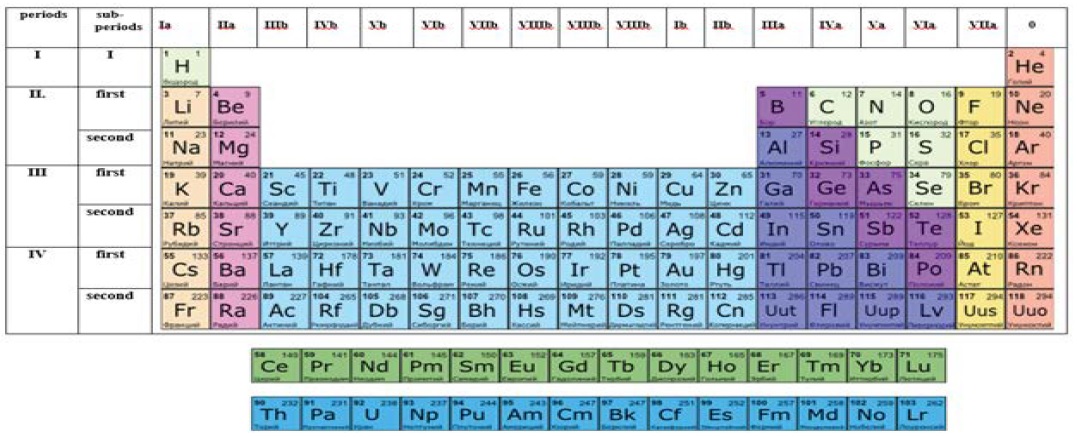
Therefore, if we assume the possibility of division of levels into two sublevels, as is generally adopted by chemical engineers, there arise grounds for qualitative rearrangement of periods in the Mendeleev’s table. The major ground for that can be the requirement that infill of electron shells should run sequentially, following the general principles of building their electron configurations. Then, basing on the general principle of building electron shells and therefore correction of the Mendeleev’s table, we suggest the following. Numbers of periods, as that should be, need to be equated to the value of the principle quantum number and to the correspondence with other calculations represented in (Table 2). Then the Mendeleev’s table will take the form shown in (Figure 2).

Since sublevels with the same number of electrons are close among one another by their electron structure, they should be distinguished depending on the sequence of the infill of their electron sublayers. To that end, the words first (first) or (second) should be inserted into their electron formula prior to the respective sublevel. Thus, we introduce two new provisionally named quantum states for electronic layers of all the periods except the first. For instance, for Borium the electron formula will take the following form: В-1s2 first2s2 2p1, and for silicon: Si- 1s2 first2s2 2p6 second 2s2 2p2. etc... etc.

In general, the listed additions into the Mendeleev’s table shown in (Figure 2) should be better examined on the example of a long version of this table. The suggested innovations are just distinctly seen in that version. In particular, the order of infill of the respective periods of the table with electrons becomes clear. At the same time, for instance, infill of the second period will be running sequentially for similar first and second sublevels containing 2s and 6p electrons each. In the Mendeleev’s table, these sublevels were independent (2 and 3 period) and for that reason there were no proper explanation to the absence of 3d electrons in the 3 period and presence of 3d electrons in the electron formulas of elements of 4th period of the classical Mendeleev’s table.

Merging of the 4 and 5 periods of the traditional Mendeleev’s table into one common 3 period, as per our suggestion, allows correcting that issue and bringing the sequence of infill of the electron shells of atoms of that suggested period into a proper order of priority. In both subperiods of the period, the sequence of infill will be similar and consecutive first 3s2 3d103p6 and second 3s2 3d103p6. In our opinion, precisely the same will occur during the merging of 6 and 7 periods of the existing system into one common 4 period. But in that case we will have to take the existence of f electrons into account. However, that will in no way affect the order of priority and sequence of infill of the period subperiods with electrons.

The additions to the Mendeleev’s table suggested by us also make it possible to draw a conclusion on the sequence of infill of electron orbitals of element atoms. Apparently, and as follows from (Figure 2), infill of the electron shells starts with S-orbitals, then (except the elements of 2 period) the d and f orbitals are filled, and only р orbitals are filled at the end. Such an order of infill is quite logical since all the major distinctive chemical properties of metals and nonmetals are mainly related just to the electrons of s, p orbitals. As regards the d and f orbitals, the chemical properties of most metals which take a special place in the periodic table (Figure 2) are related to these orbitals.

Therefore, all the above allows highlighting the following points:

Therefore, the numbers of periods are reduced to four. Introduction of the first and second subperiods allows meeting the requirement of the Pauli exclusion principle in new conditions. At the same time, the principle quantum number of the chemical elements of a period, which characterizes the energy of electron shell, remains unchanged, but the newly suggested quantum states of sublevels denoted as first and second do change. Therefore, the provision stating that electrons can be inside the atom at strictly admitted orbits holds and is complemented by introduction of the notion “quantum state of a sublevel” to the already existing ones. Then the order of formation of electron layers will be as follows: the principle quantum number (n), followed by the quantum state of a subperiod (first or second) in a period, and then all the remaining quantum orbitals;

By the “quantum state” expression we suggest designating two sequentially infilled sublevels in each of the newly viewed periods in which the configuration of electron subshell corresponding thereto is retained and duplicated.

It should be also added that formula (II) and the changed Mendeleev’s table (Figure 2) allows counting the hypothetic quantities of g-orbitals and electrons of the V period. (Table 2) represents the number of electrons (50) at each of the hypothetic sublevels of that period. And since the s, d, f- and p-orbitals have 32 electrons in the total, then the difference in 18 electrons makes the total number of electrons at the respective 9 g-orbitals.