The shortcomings of the well-known solution of the Maxwell equations for a spherical wave are indicated. A new strict solution of these equations is proposed. This solution, when applied in antenna design systems, should allow more formalization of the antenna design process and should improve the quality of the antennas.

Antenna design, Maxwell’s equation, Spherical coordinates.

The shortcomings of the well-known solution of the Maxwell equations for a spherical wave are indicated. A new strict solution of these equations is proposed. This solution, when applied in antenna design systems, should allow more formalization of the antenna design process and should improve the quality of the antennas.

Antenna design, Maxwell’s equation, Spherical coordinates.

The solution of the Maxwell equations for a spherical wave is necessary for the design of antennas. Such a problem arises in the solution of the equations of electrodynamics for an elementary electric dipole - a vibrator. The solution of this problem is known and it is on the basis of this solution that the antennas are constructed. At the same time, this solution has a number of shortcomings, in particular [1-4],

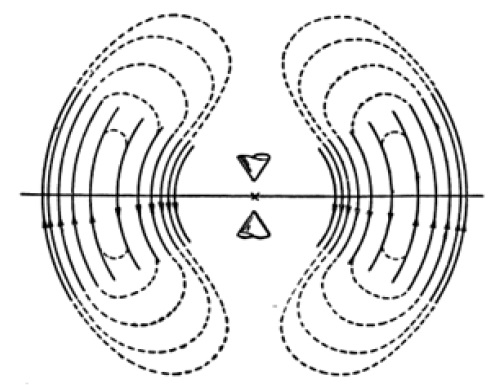
In Figure 1 [4] the picture of the lines of force of the electric field, constructed on the basis of the known solution is shown. Obviously, such a picture can not exist in a spherical wave.

Far from the vibrator-in the so-called the far zone, where longitudinal (directed along the radius) the electric and magnetic intensities can be neglected by, the solution of the problem is simplified. But even there the well-known solution has a number of shortcomings [1-4]. The main disadvantages of this solution are that

These shortcomings are a consequence of the fact that until now Maxwell’s equations for spherical coordinates could not be solved. A well-known solution is obtained after dividing the entire domain into so-called near, middle and far zones and after applying a variety of assumptions, different for each of these zones.

In practice, specified drawbacks of the known solution mean that they (mathematical solutions) do not strictly describe the real characteristics of technical devices. A more rigorous solution, obtained in [5], when applied in the design systems of such devices, must certainly improve their quality. This solution is briefly described below.

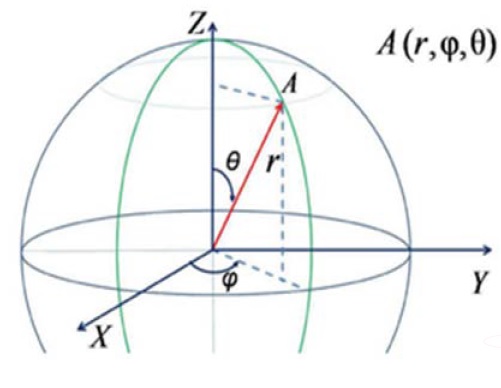
In Figure 2, the system of spherical coordinates ($\rho ,\theta ,\varphi$) are shown.

Next, we will place the formulas in tables and use the following notation:

T (table_number) - (column_number) - (line_number) Table 1 (Eq. 1-3) lists the expressions for the rotor and the divergence of the vector E in these coordinates [6]. Here and below

We establish the following notation:

$$\text{Ψ}\left(E_{\rho }\right)=\frac{E_{\rho }}{\rho }+\frac{\partial E_{\rho }}{\partial \rho }\left(1\right)$$

$$T\left(E_{\phi }\right)=\left(\frac{E_{\phi }}{\text{tg}\left(\theta \right)}+\frac{\partial \left(E_{\phi }\right)}{\partial \left(\theta \right)}\right)\left(2\right)$$

With these designations taken into account, the formulas in Table 1 take the form given in Table 1. In the Table 2 we write the Maxwell equations.

Thus, there are eight Maxwell equations with six unknowns. This system is overdetermined. We have to admit that in a spherical wave there are radial intensities. However, even so, the system of Maxwell’s equations remains redefined.

Let us also assume that there are radial electric currents of displacement. This assumption does not remove the problem of over determination, but adds one more problem. The point is that the sphere has an ideal symmetry and the solution must obviously be symmetrical.

It is suggested that there are also radial magnetic displacement currents. Such an assumption does not require the existence of magnetic monopoles as well; the existence of electric displacement currents does not follow from the existence of electric charges.

Next, we will look for the solution in the form of the functions E, H, J, M, presented in Table 3 (Eq. 2), where the actual functions of the form $g\left(\theta \right)$ and $e\left(\rho \right), h\left(\rho \right),j\left(\rho \right),m\left(\rho \right)$ are to be calculated, and the coefficients $\propto , \omega$ are known.

Under these conditions, we transform the formulas from Table 1 (Eq. 3 and 4), where the following notations are adopted:

$$\boxed{e_{\phi }}=\frac{\partial \left(e_{\phi }\left(\rho \right)\right)}{\partial \left(\rho \right)},\left(3\right)$$

$$q=\chi \rho +\omega t\left(4\right)$$

(2, 4) we find:

$$T\left(E_{\phi }\right)=\left(\frac{\text{sin}\left(\theta \right)}{\text{tg}\left(\theta \right)}+\text{cos}\left(\theta \right)\right)e_{\phi }\text{cos}(q)=2e_{\phi }\text{cos}\left(\theta \right)\text{cos}(q)\left(5\right)$$

Similarly,

$$T\left(E_{\theta }\right)=2e_{\theta }\text{cos}\left(\theta \right)\text{sin}\left(q\right)\left(6\right)$$

$$T\left(H_{\phi }\right)=2h_{\phi }\text{cos}\left(\theta \right)\text{sin}\left(q\right)\left(7\right)$$

$$T\left(H_{\theta }\right)=2h_{\theta }\text{cos}\left(\theta \right)\text{cos}\left(q\right)\left(8\right)$$

With these designations taken into account, the formulas in Table 1 (Eq. 1-3) take the form given in Table 1 (Eq. 1-4). In Table 2 (Eq. 2) we write the Maxwell equations taking into account the radial displacement currents. Further, we take condition

$$\alpha =0\left(9\right)$$

We substitute the rotors and divergences from Table 1 (Eq. 4) into Table 2 (Eq. 2) equations, take into account condition (9). Then, after cumbersome transformations, the equations in Table 2 (Eq. 2) is shortened and the system of equations takes the form shown in Table 3 and 4 (Eq. 2). This system of equations has the following solution:

$$\chi =\frac{\omega }{c}\sqrt{\epsilon \mu }\left(10\right)$$

$$e_{\phi }=A/\rho , e_{\theta }=A/\rho ,\left(11\right)$$

$${\text{h}}_{\text{φ}}=-\text{B}/\text{ρ},{\text{ h}}_{\text{θ}}=\text{B}/\text{ρ},\left(12\right)$$

$$\frac{\text{B}}{\text{A}}=\sqrt{\frac{\text{ε}}{\text{μ}}}\left(13\right)$$

Here A and B are constants. The functions $h_{\rho }, e_{\rho }$ are solutions of the differential equations of the following form:

$$\boxed{\boxed{e_{\rho }}}+\frac{2}{\rho }\boxed{e_{\rho }}+{\chi }^2{e}_{\rho }-\frac{2A}{{\rho }^3}=0,\left(14\right)$$

$$\boxed{\boxed{h_{\rho }}}+\frac{2}{\rho }\boxed{h_{\rho }}+{\chi }^2{h}_{\rho }-\frac{2B}{{\rho }^3}=0\left(15\right)$$

After this, the functions $j_{\rho }\left(\rho \right)$, ${\overline{J}}_{{}_{\rho }}\left(\rho \right)$, $m_{\rho }\left(\rho \right)$, ${\overline{m}}_{\rho }\left(\rho \right)$ can be found using the equations in Table 4 (Eq. 2.1 and 2.5).

In particular, for $\text{ε}=\text{μ}$ , for example, for a vacuum, we find from previous equations that A=B and

$$h_{\rho }=e_{\rho }\left(16\right)$$

In particular, for A=B and a small value of χ , these functions take the following form:

$$h_{\rho }=e_{\rho }=-\frac{1}{\rho }\left(G+2A\times ln\left(\rho \right)\right),\left(17\right)$$

$${\overline{h}}_{\rho }={\overline{e}}_{\rho }=\frac{D}{\rho }\left(18\right)$$

$$j_{\rho }=\frac{2A}{{\rho }^2}-\frac{\mu \omega }{c}\times \frac{D}{\rho } ,\left(19\right)$$

$${\overline{j}}_{\rho }=-\frac{\mu \omega }{c}\times \frac{1}{\rho }\left(G+2A\times ln\left(\rho \right)\right)\left(20\right)$$

$$m_{\rho }=-\frac{2B}{{\rho }^2}+\frac{\epsilon \omega }{c}\times \frac{D}{\rho } ,\left(21\right)$$

Here G is a constant that can take different values for the functions $e_{\rho }$ and $h_{\rho }$ , D is a constant that can take different values for the functions ${\overline{e}}_{\rho }$ and ${\overline{h}}_{\rho }$ .

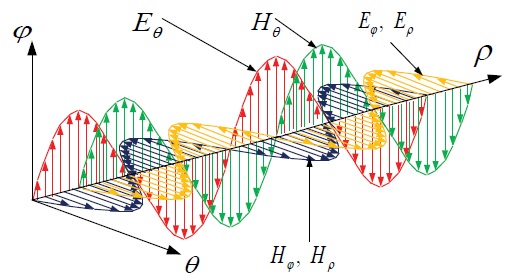
Thus, the system of Maxwell equations in spherical coordinates has a solution presented in Table 3 (Eq. 2), where the unknowns are determined from (10-15, Table 4 (Eq. 2.1 and 2.5). The main properties of this solution are as follows (Figure 3):

Therefore, based on the solution found, it is advisable to begin developing a new system for the automated design of antennas.

On the basis of this same theory, the problem of detecting the position of the radiation source by measuring the intensities of the electromagnetic field in a limited region of the radar can be solved.