Total potential energy was formed based on the traditional refined plate theory assumptions. Displacement field, kinematic relations, constitutive relations, stress displacement relations were derived from the deformed section of a thick anisotropic plate respectively. Strain energy was formed by substituting the kinematic relations and stressdisplacement relations into the universal strain energy equation. By the addition of the external work to the strain energy equation, total potential energy functional for analysis of thick anisotropic rectangular plate was obtained. The total potential energy functional were minimized by differentiating it with respect to the deflection, shear deformation rotation in x direction and shear deformation rotation in y direction respectively. This yielded the governing equation and two compatibility equations of thick anisotropic rectangular plate. A third order polynomial shear deformation function was derived from shear stress across the thickness of a rectangular plate section. The third order polynomial shear deformation function was employed to the governing equation and compatibility equation to obtain the displacement function (deflection, shear deformation rotation in x direction and shear deformation rotation in y direction). The general displacement functions obtained were used to satisfy the specified boundary conditions which gave the unique displacement functions for the various plate, (ssss), (cccc), (ccss), (cscs), (cccs), (csss), (ssfs), (ccfc), (csfs), (scfs), (scfc), (ccfs) respectivelyssss. Stiffness coefficients for various plate with their unique displacement functions were calculated. Minimizing total potential energy functional with respect to the coefficients of the displacement functions gave the formula for calculating the coefficients of the displacements and other formulas to calculate the displacements and stresses of the anisotropic thick plate. These formulas derived herein were used to analyze typical anisotropic rectangular thick plates. The numerical results obtained for displacements (w) were in good agreement with previous work by other scholars.

Total potential energy, Materials, Composite structural elements, Anisotropic plates.

Total potential energy was formed based on the traditional refined plate theory assumptions. Displacement field, kinematic relations, constitutive relations, stress displacement relations were derived from the deformed section of a thick anisotropic plate respectively. Strain energy was formed by substituting the kinematic relations and stressdisplacement relations into the universal strain energy equation. By the addition of the external work to the strain energy equation, total potential energy functional for analysis of thick anisotropic rectangular plate was obtained. The total potential energy functional were minimized by differentiating it with respect to the deflection, shear deformation rotation in x direction and shear deformation rotation in y direction respectively. This yielded the governing equation and two compatibility equations of thick anisotropic rectangular plate. A third order polynomial shear deformation function was derived from shear stress across the thickness of a rectangular plate section. The third order polynomial shear deformation function was employed to the governing equation and compatibility equation to obtain the displacement function (deflection, shear deformation rotation in x direction and shear deformation rotation in y direction). The general displacement functions obtained were used to satisfy the specified boundary conditions which gave the unique displacement functions for the various plate, (ssss), (cccc), (ccss), (cscs), (cccs), (csss), (ssfs), (ccfc), (csfs), (scfs), (scfc), (ccfs) respectivelyssss. Stiffness coefficients for various plate with their unique displacement functions were calculated. Minimizing total potential energy functional with respect to the coefficients of the displacement functions gave the formula for calculating the coefficients of the displacements and other formulas to calculate the displacements and stresses of the anisotropic thick plate. These formulas derived herein were used to analyze typical anisotropic rectangular thick plates. The numerical results obtained for displacements (w) were in good agreement with previous work by other scholars.

Total potential energy, Materials, Composite structural elements, Anisotropic plates.

Technological progress is associated with continuous improvement of existing material properties and this has led to the expansion of structural material classes and types. Usually new materials emerge due to the need to improve structural efficiency and performance. These new materials in turn provide opportunities to develop outdated structures and technologies, and also create new problems and tasks to engineers and material scientists. One of the best manifestations of these related processes is the development of the composite structural elements which are associated with the anisotropic structural plate, to which this study is devoted.

Composite materials emerged in the middle of the twentieth century as a promising class of engineering materials providing new prospects for modern technology. Broadly speaking, any material consisting of two or more components with different properties and distinct boundaries between the components can be referred to as a composite material [1].

The sudden increase in the use of anisotropic or composite materials in many types of engineering structures (e.g., high rise structures, aerospace, underwater structures, automotive, electronic circuit board, medical prosthetic devices and sports equipment) and the number of journals and research papers published in the last two decades attest to the fact that there has been a major effort to develop composite material systems, and to analyze and design structural components made from composite materials [2]. The production of anisotropic material involves chemists, electrical engineers, chemical engineers, material scientists, mechanical engineers and structural engineers. Structural engineer deals mainly with the analysis and design of these anisotropic materials.

Anisotropic plates are plates with different resistance to mechanical actions in different directions. This implies that anisotropic plates are directionally dependent as opposed to isotropic plates that implies identical properties in all directions. Examples of such plates are aviation plywood, delta wood, coated aluminum plate, alloyed metal plates and a number of other materials [3].

A plate is a structural member that is bounded by two flat surfaces, which are separated by thickness (t) [4]. Plates are widely used in many engineering applications and specifically in aeronautic, electronic, marine, mechanical and civil engineering for the construction of aircraft, circuit board, ships, bridges, vehicles, satellites, platforms, building floors and roofs, shear walls, computer hard-disk drives and other complex structures [5-7]. The x-axis and y-axis are the in-plane axes while the z- axis is the out of plane axis. The thickness (t) is small compared with the in-plane surface dimensions ‘a’ and ‘b’ [8]. The thickness is usually constant but may be variable and is measured normal to the middle surface of the plate. When the plate thickness is divided equally by a plane parallel to its surface, this plane is referred to as middle surface [9,10]. A plate is regarded as thick plate when the span-depth ratio is less than or equal to 10 (α ≤ 10) while the plate will be idealized to be thin when the span-depth ratio varies between 10 and 100 (10 ≤ α ≤ 100) [11]. However, it has become common knowledge that the true range of span-depth ratio for thin plate is between 50 and 100 (50 ≤ α ≤ 100). The range between 10 and 50 can be classified as moderately thick plates while the range of span-depth ratio exceeding 100 is used to classify membrane plates [4]. Thin plates are analyzed based on classical plate theory, while thick plates are analyzed based on refined plate theories [4,12-16]. Both the analysis of thick plate and thin plate had for long been based on the trigonometric displacement functions until recently when Ibearugbulem et al. [17] and Ibearugbulem [18] popularized the use of orthogonal polynomial functions in plate analysis. Hence, this work shall base it analysis of plate on orthogonal polynomial functions.

The classical plate theory assumed that the plane cross sections that are initially normal to the plate’s mid-surface before deformation remain plane and normal to the midsurface after deformation. This is because the transverse shear strains were neglected. However, significant transverse shear strains occur in thick and moderately thick plates. Hence, the theory gives inaccurate results for the plates. Therefore, the shear strains have to be taken into account. One of the numerous theories of plates that include the transverse shear strains is the Reissner and Mindlin theory, known as the first-order shear deformation theory, which defines the displacement field as linear variations of midplane displacements. This theory, in which the relationship between the resultant shear forces and the shear strains is obtained by using shear correction factors, has some advantages due to its simplicity and low computational cost. Some other plate theories, namely the higher-order shear deformation theories, include the effect of transverse shear strains. The static or dynamic loads carried by plates are predominantly perpendicular to the plate faces. The loadcarrying action of a plate is similar, to that of beams or cables to a certain extent; thus, plates can be approximated by a gridwork of an infinite number of beams or by a network of an infinite number of cables, depending on the flexural rigidity of the structures [11].

Works on refined plate theory have been characterized by the use of trigonometric displacement function. Many scholars have obtained the closed form solutions and others have obtained approximate solution using assumed displacement functions in energy method. However, one thing that is common in them all is the use of trigonometric displacement functions to approximate the deformed shapes of the plates [12,13,19-29]. Others have applied the assumed polynomial displacement functions in numerical methods like finite element method and differential quadrature element methods [30-37]. The major flaw in their traditional refined plate theory (Third order or higher order shear deformation theory) is the assumption of their displacement functions in their thick anisotropic plate analysis. These assumptions has never been solved to ascertain its validity or correctness in thick anisotropic plate analysis.

Assumptions: This work shall be based on the traditional refined plate theory assumptions as stated below:

a) The displacements, u, v and w are small when compared with plate thickness.

b) The in-plane displacements, u and v are differentiable in x, y and z axes, while the out-of-plane displacement (deflection), w is only differentiable in x and y axes. This means that the first derivative of w with respect to z is zero. Consequently, the vertical strain, εz=0.

c) The effect of the out-of-plane normal stress on the gross response of the plate is small when compared with other stresses. Thus, it can be neglected. That is, σz=0.

d) The vertical line that is initially normal to the middle surface of the plate before bending is no longer straight nor normal to the middle surface after bending. The line is now parabolic. That is, φ ≠ θc. where φ is the total rotation of the middle surface in this case and θc is the classical plate theorem rotation of the middle surface.

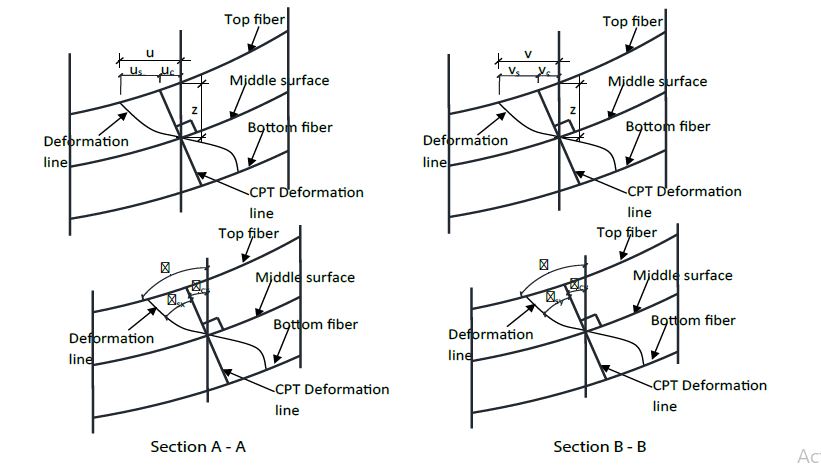
Here effort shall be made to formulate the direct governing equation for an anisotropic thick plate under pure bending. In doing so Figure 1, Figure 1a and Figure 1b shall be relied upon.

Displacement field: The refined plate theory (RPT) inplane displacements, u and v are defined mathematically from Figure 1 as presented:

$$u=u_c+u_s$$ (1)

$$v=v_c+v_s$$ (2)

Where u and v are the in-plane displacement in x direction y direction respectively, and the out of plane displacement (deflection) is taken as “w”.

Where;

CPT: Classical Plate Theory

: Total rotation of the middle surface

θ_cx and θ_cy : Classical plate theorem rotation of the middle surface.

θ_sx and θ_sy : Angle between the CPT deformation line and the shear deformation line.

u_c and v_c : In-plane displacement due to classical plate theory.

u_s and v_s : In-plane displacement due to shear deformation theory.

The classical part of the in-plane displacements uc and vc are defined as follows:

$$u_c=-z{\theta }_{cx}=-z\frac{dw}{dx}$$ (3)

$$v_c=-z{\theta }_{cy}=-z\frac{dw}{dy}$$ (4)

Analogously, the shear deformation part of the in-plane displacements us and vs are defined as:

$$u_s=F(z){\theta }_{sx}$$ (5)

$$v_s=F(z){\theta }_{sy}$$ (6)

Where; θ_sx =φ_x = shear rotation in x – direction

θ_sy =φ_y = shear rotation in y – direction

F (z) is used in Equations (5) and (6) instead of z due to the fourth assumption in section 3.1.1 (Figure 1).

Substituting equations (3) to (6) into equations (1) and (2), we obtain;

$$U=-Z\frac{\partial w}{\partial x}+F(z).{\varphi }_x$$ (7)

$$V=-Z\frac{\partial w}{\partial y}+F(z).{\varphi }_y$$ (8)

Having stated the in-plane displacement functions, the work will proceed to kinematic relations.

Strain-displacement relations (kinematic relations): The strain-displacement relations suitable for small deflection of thick anisotropic rectangular plates will be considered. From the second assumption in section 3.1.1, the vertical strain εz, is equal to zero. Thus, the remaining five engineering strain components are derived differentiating equation (7) and (8) with respect to x and y appropriately;

$${\epsilon }_x=\frac{du}{dx}=-z\frac{d^{2}w}{d{x}^2}+F(z)\frac{d\varphi x}{dx}$$ (9)

$${\epsilon }_y=\frac{dv}{dx}=-z\frac{d^{2}w}{d{y}^2}+F(z)\frac{d\varphi y}{dy}$$ (10)

$$\begin{array}{l}{\gamma }_{xy}=\frac{du}{dy}+\frac{dv}{dx}=-z\frac{d^{2}w}{dxdy}+F(z)\frac{d\varphi x}{dy}+-z\frac{d^{2}w}{dxdy}\\ +F(z)\frac{d\varphi y}{dx}=-2z\frac{d^{2}w}{dxdy}+F(z)\frac{d\varphi x}{dy}+F(z)\frac{d\varphi y}{dx}\end{array}$$ (11)

$$\begin{array}{l}{\gamma }_{xz}=\frac{du}{dz}+\frac{dw}{dx}=-\frac{dw}{dx}+\frac{dF(z)}{dz}{\varphi }_x\\ +\frac{dw}{dx}=\frac{dF(z)}{dz}{\varphi }_x\end{array}$$ (12)

$$\begin{array}{l}{\gamma }_{yz}=\frac{dv}{dz}+\frac{dw}{dy}=-\frac{dw}{dy}+\frac{dF(z)}{dz}{\varphi }_y\\ +\frac{dw}{dy}=\frac{dF(z)}{dz}{\varphi }_y\end{array}$$ (13)

Constitutive relations (Stress-Strain Relations): The work shall apply Hook and Poisson’s theorems to obtain the stress - strain relations. It shall also make use of only five stress components (σ_x, σ_y, τ_xy, τ_xz and τ_yz) and corresponding five strain components (τ_yz, ε_x, γ_xy, γ_xz, and γ_yz) as given;

$${\epsilon }_1=\frac{{\sigma }_1}{E_1}-\frac{v_2{\sigma }_2}{E_2}$$ (14)

$${\epsilon }_2=\frac{V_1{\sigma }_1}{E_1}+\frac{{\sigma }_2}{E_2}$$ (15)

$${\gamma }_{12}=\frac{{\tau }_{12}}{G_{12}}$$ (16)

$${\gamma }_{13}=\frac{{\tau }_{13}}{G_{13}}$$ (17)

$${\gamma }_{23}=\frac{{\tau }_{23}}{G_{23}}$$ (18)

lets,$$\frac{E_1}{V_1}-\frac{E_2}{V_2}=E_{12}$$ (19)

Thus, equation (14) and (15) can be rewritten as;

$${\epsilon }_1=\frac{{\sigma }_1}{E_1}-\frac{{\sigma }_2}{E_{12}}$$ (20)

$${\epsilon }_1=-\frac{{\sigma }_1}{E_{12}}+\frac{{\sigma }_2}{E_2}$$ (21)

Multiplying equation (21) by $$\frac{E_{12}}{E_1}$$ gives

$$\frac{{\epsilon }_2{E}_{12}}{E_1}=-\frac{{\sigma }_1{E}_{12}}{E_2{E}_{12}}+\frac{{\sigma }_2{E}_{12}}{E_1{E}_2}=-\frac{{\sigma }_1}{E_1}+\frac{{\sigma }_2{E}_{12}}{E_1{E}_2}$$ (22)

Adding equations (20) and equations (22) gives;

$${\epsilon }_1+\frac{{\epsilon }_2{E}_{12}}{E_1}=\frac{{\sigma }_1}{E_1}-\frac{{\sigma }_1}{E_1}+\frac{{\sigma }_2{E}_{12}}{E_1{E}_2}-\frac{{\sigma }_2}{E_{12}}$$

$${\epsilon }_1+\frac{{\epsilon }_2{E}_{12}}{E_1}={\sigma }_2\left[\frac{E_{12}}{E_1{E}_2}-\frac{1}{E_{12}}\right]$$ (23)

Substituting equation (19) into equation (23) appropriately gives;

$${\epsilon }_1+\frac{{\epsilon }_2}{V_1}={\sigma }_2\left[\frac{1}{V_1{E}_2}-\frac{1}{E_{12}}\right]$$ (24)

$${\epsilon }_1+\frac{{\epsilon }_2}{V_1}=\frac{{\sigma }_2}{V_1{E}_2{E}_{12}}\left[E_{12}-V_1{E}_2\right]$$ (25)

$${\epsilon }_1{V}_1{E}_2{E}_{12}+{\epsilon }_1{E}_2{E}_{12}={\sigma }_2\left[E_{12}-V_1{E}_2\right]$$ (26)

Substituting equation (19) into equation (26) appropriately gives;

$$\begin{array}{l}{\epsilon }_1{V}_1{E}_2\frac{E_1}{V_1}+{\epsilon }_2{E}_2\frac{E_1}{V_1}={\sigma }_2\left[\frac{E_1}{V_1}-V_1{E}_2\right]\\ ={\sigma }_2\left[\frac{E_2}{V_2}-V_1{E}_2\right]\end{array}$$ (27)

$$E_1{E}_2\left[{\epsilon }_1+\frac{{\epsilon }_2}{V_1}\right]=\frac{{\sigma }_2{E}_2}{V_2}\left[1-V_1{V}_2\right]$$

$$E_1\left[{\epsilon }_1+\frac{{\epsilon }_2}{V_1}\right]=\frac{{\sigma }_2}{V_2}\left[1-V_1{V}_2\right]$$

$$\begin{array}{l}\frac{E_1}{V_1}\left[{\epsilon }_1{V}_1+{\epsilon }_2\right]=\frac{{\sigma }_2}{V_2}\left[1-V_1{V}_2\right]\\ =E_{12}\left[{\epsilon }_1{V}_1+{\epsilon }_2\right]\end{array}$$

$${\sigma }_2=\frac{E_{12}{V}_2}{\left[1-V_1{V}_2\right]}+\left[V_1{\epsilon }_1+{\epsilon }_2\right]$$ (28)

Similarly;

$${\sigma }_1=\frac{E_{12}{V}_1}{\left[1-V_1{V}_2\right]}+\left[{\epsilon }_1+V_2{\epsilon }_2\right]$$ (29)

Expanding equation (28) and equation (29) gives respectively

$${\sigma }_2=\frac{E_{12}{V}_1{\epsilon }_1}{\left[1-V_1{V}_2\right]}+\frac{E_{12}{V}_2{\epsilon }_2}{\left[1-V_1{V}_2\right]}$$ (30)

$${\sigma }_1=\frac{E_{12}{V}_1{\epsilon }_1}{\left[1-V_1{V}_2\right]}+\frac{E_{12}{V}_1{V}_2{\epsilon }_2}{\left[1-V_1{V}_2\right]}$$ (31)

Also, from equations (16), (17) and equation (18) we have;

$${\tau }_{12}=G_{12}{\gamma }_{12}$$ (32)

$${\tau }_{13}=G_{13}{\gamma }_{13}$$ (33)

$${\tau }_{23}=G_{23}{\gamma }_{23}$$ (34)

Casting equations (30), (31), (32), (33) and (34) into matrix form gives;

$$\left[\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\tau }_{12}\\ {\tau }_{13}\\ {\tau }_{23}\end{array}\right]=\left[\begin{array}{ccccc}\frac{E_{12}{V}_1}{1-V_1{V}_2}& \frac{E_{12}{V}_1{V}_2}{1-V_1{V}_2}& 0& 0& 0\\ \frac{E_{12}{V}_1{V}_2}{1-V_1{V}_2}& \frac{E_{12}{V}_2}{1-V_1{V}_2}& 0& 0& 0\\ 0& 0& G_{12}& 0& 0\\ 0& 0& 0& G_{13}& 0\\ 0& 0& 0& 0& G_{23}\end{array}\right]\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\gamma }_{12}\\ {\gamma }_{13}\\ {\gamma }_{23}\end{array}\right]$$ (35)

From equation (35) we obtained equation (36) as given;

$$\left[\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\tau }_{12}\\ {\tau }_{13}\\ {\tau }_{23}\end{array}\right]=\left[\begin{array}{ccccc}{A}_{11}& A_{12}& 0& 0& 0\\ A_{12}& A_{22}& 0& 0& 0\\ 0& 0& A_{33}& 0& 0\\ 0& 0& 0& A_{44}& 0\\ 0& 0& 0& 0& A_{55}\end{array}\right]\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\gamma }_{12}\\ {\gamma }_{13}\\ {\gamma }_{23}\end{array}\right]$$ (36)

Where;

$$\begin{array}{l}{A}_{11}=\frac{E_{12}{V}_1}{1-V_1{V}_2};A_{12}=\frac{E_{12}{V}_1{V}_2}{1-V_1{V}_2}=A_{21};A_{22}\\ =\frac{E_{12}{V}_2}{1-V_1{V}_2};A_{33}=G_{12};A_{44}=G_{13};A_{55}=G_{23}\end{array}$$

Equation (36) can be put in short form as:

$$\left[{\sigma }_{12}\right]=\left[A\right]\left[{\gamma }_{12}\right]$$ (37)

The X-Y planer form of equation (37) is:

$$\left[{\sigma }_{xy}\right]=\left[B\right]\left[{\gamma }_{xy}\right]$$ (38)

Where;

$$[B]={[T]}^{(-1)}[A][T]$$ (39)

Equation (39) is the transformational matrix equation Where;

$$T=\left[\begin{array}{ccccc}{M}^2& n^2& -2Mn& 0& 0\\ n^2& M^2& 2Mn& 0& 0\\ Mn& -Mn& (M^2-n^2)& 0& 0\\ 0& 0& 0& M& -n\\ 0& 0& 0& n& M\end{array}\right]$$ (40)

$${[T]}^{-1}=\left[\begin{array}{ccccc}{M}^2& n^2& -2Mn& 0& 0\\ n^2& M^2& 2Mn& 0& 0\\ Mn& -Mn& (M^2-n^2)& 0& 0\\ 0& 0& 0& M& -n\\ 0& 0& 0& n& M\end{array}\right]$$ (41)

$$A=\left[\begin{array}{ccccc}\frac{E_{12}{v}_1}{1-v_1{v}_2}& \frac{E_{12}{v}_1{v}_2}{1-v_1{v}_2}& 0& 0& 0\\ \frac{E_{12}{v}_1{v}_2}{1-v_1{v}_2}& \frac{E_{12}{v}_1}{1-v_1{v}_2}& 0& 0& 0\\ 0& 0& G_{12}& 0& 0\\ 0& 0& 0& G_{13}& 0\\ 0& 0& 0& n& G_{23}\end{array}\right]$$ (42)

Substituting equation (40), (41) and (42) into equation (39) gives:

$$[B]=\left[\begin{array}{ccccc}{B}_{11}& B_{12}& B_{13}& 0& 0\\ B_{21}& B_{22}& B_{23}& 0& 0\\ B_{31}& B_{32}& B_{33}& 0& 0\\ 0& 0& 0& B_{44}& B_{45}\\ 0& 0& 0& B_{54}& B_{55}\end{array}\right]$$ (43)

Where;

$$B_{11}=M^4{A}_{11}+M^2{n}^2(2A_{12}+2A_{33})+A_{22}{n}^4$$

$$B_{12}=M^2{n}^2(A_{11}+A_{22}-2A_{33})+A_{12}(n^4+M^4)$$

$$\begin{array}{l}{B}_{13}=2M^{3}n(A_{11}-A_{12}-A_{33})\\ +2M{n}^3(A_{12}-A_{22}+A_{33})\end{array}$$

$$\begin{array}{l}{B}_{21}=M^2{n}^2(A_{11}+A_{22}-2A_{33})\\ +A_{12}(n^4+M^4)=B_{12}\end{array}$$

$$B_{22}=n^4{A}_{11}+2M^2{n}^2(A_{12}+A_{33})+A_{22}{M}^4$$

$$\begin{array}{l}{B}_{23}=2n^{3}M(A_{11}-A_{12}-A_{33})\\ +2n{M}^3(A_{12}-A_{22}+A_{33})\end{array}$$

$$\begin{array}{l}{B}_{31}=M^{3}n(A_{11}-A_{12}-A_{33})\\ +M{n}^3(A_{12}-A_{22}+A_{33})=\frac{B_{13}}{2}\end{array}$$

$$\begin{array}{l}{B}_{32}=n^{3}M(A_{11}-A_{12}-A_{33})\\ +n{M}^3(A_{12}-A_{22}+A_{33})=\frac{B_{23}}{2}\end{array}$$

$$\begin{array}{l}{B}_{33}=2M^2{n}^2(A_{11}-2A_{12}+A_{22}-A_{33})\\ +A_{33}(n^4+M^4)\end{array}$$

$$B_{44}=M^2{A}_{44}+A_{55}{n}^2$$

$$B_{45}=Mn{A}_{44}-Mn{A}_{55}=Mn(A_{44}-A_{55})=B_{54}$$

$$B_{54}=Mn{A}_{44}-Mn{A}_{55}=Mn(A_{44}-A_{55})=B_{45}$$

$$B_{55}=n^2{A}_{44}+A_{55}{M}^2$$

$$M=cos\theta ;n=sin\theta$$

Where θ is the angle of inclination of the plate fibers on the x axis.

Strain energy^U : To obtain the strain energy equation for thick anisotropic plate analysis, the work shall proceed by substituting the kinematic relations and stress- displacement relations into the universal strain energy equation given as;

$$\begin{array}{l}U=\frac{1}{2}{\int }_x{\int }_y[{\int }_z\sigma .\epsilon dz]dxdy\\ =\frac{1}{2}{\int }_x{\int }_y[{\int }_z({\sigma }_x{\epsilon }_x+{\sigma }_y{\epsilon }_y\\ +{\tau }_{xy}{\gamma }_{xy}+{\tau }_{xz}{\gamma }_{xz}+{\tau }_{yz}{\gamma }_{yz})dz]dxdy\end{array}$$ (43a)

External work, V: For the proposed study, the external work V due to the uniformly distributed normal (lateral) load “q” is given as;

$$V=-q{\int }_0^a{\int }_0^b(w)\partial x\partial y$$ (43b)

Stress–Displacement relations: Kinematic equations shall be substituted into the constitutive equations to obtain the stress – displacement relations as shown;

$${\sigma }_x=B_{11}{\epsilon }_x+B_{12}{\epsilon }_y+B_{13}{\gamma }_{xy}$$ (44)

$${\sigma }_y=B_{21}{\epsilon }_x+B_{22}{\epsilon }_y+B_{23}{\gamma }_{xy}$$ (45)

$${\tau }_{xy}=B_{31}{\epsilon }_x+B_{32}{\epsilon }_y+B_{33}{\gamma }_{xy}$$ (46)

$${\tau }_{xz}=B_{44}{\gamma }_{xz}+B_{45}{\gamma }_{yz}$$ (47)

$${\tau }_{yz}=B_{54}{\gamma }_{xz}+B_{55}{\gamma }_{yz}$$ (48)

$$\begin{array}{l}{\sigma }_x{\epsilon }_x=B_{11}{\epsilon }_x{\epsilon }_x+B_{12}{\epsilon }_y{\epsilon }_x\\ +B_{13}{\gamma }_{xy}{\epsilon }_x\end{array}$$ (49)

$$\begin{array}{l} {\sigma }_y{\epsilon }_y=B_{21}{\epsilon }_x{\epsilon }_y+B_{22}{\epsilon }_y{\epsilon }_y\\ +B_{23}{\gamma }_{xy}{\epsilon }_y\end{array}$$ (50)

$$\begin{array}{l}{\tau }_{xy}{\gamma }_{xy}=B_{31}{\epsilon }_x{\gamma }_{xy}+B_{32}{\epsilon }_y{\gamma }_{xy}\\ +B_{33}{\gamma }_{xy}{\gamma }_{xy}\end{array}$$ (51)

$${\tau }_{xz}{\gamma }_{xz}=B_{44}{\gamma }_{xz}{\gamma }_{xy}+B_{45}{\gamma }_{yz}{\gamma }_{xz}$$ (52)

$${\tau }_{yz}{\gamma }_{yz}=B_{54}{\gamma }_{xz}{\gamma }_{yz}+B_{55}{\gamma }_{yz}{\gamma }_{xz}$$ (53)

let $$\begin{array}{l}{B}_{11}=D_{11},B_{12}=D_{12},B_{13}=D_{13},\\ B_{21}=D_{21},B_{22}=D_{22},\\ B_{23}=D_{23},B_{31}=D_{31},\\ B_{32}=D_{32}and{B}_{33}=D_{33}\end{array}$$ (54)

$$\begin{array}{l}{\epsilon }_x{}^2=Z^2{(}^{\frac{d^{2}w}{d{x}^2}}-2ZF(Z)(\frac{d^{2}w}{d{x}^2})(\frac{d{\varphi }_x}{dx})\\ +F{(}^Z{(}^{\frac{d{\varphi }_x}{dx}}\end{array}$$ (55)

$$\begin{array}{l}{\epsilon }_x{\epsilon }_y=Z^2{(}^{\frac{d^{2}w}{dxdy}}-ZF(Z)(\frac{d^{2}w}{d{x}^2})(\frac{d{\varphi }_y}{dy})\\ -ZF(Z)(\frac{d^{2}w}{d{y}^2})(\frac{d{\varphi }_x}{dx})+F{(}^Z(\frac{d{\varphi }_x}{dx})(\frac{d{\varphi }_y}{dy})\end{array}$$ (56)

$$\begin{array}{l}{\epsilon }_x{\gamma }_{xy}=2Z^2\frac{d^{2}w}{d{x}^2}.\frac{d^{2}w}{dxdy}ZF(Z)(\frac{d^{2}w}{d{x}^2})(\frac{d{\varphi }_x}{dy})\\ -ZF(Z)(\frac{d^{2}w}{d{x}^2})(\frac{d{\varphi }_y}{dx})-ZF(Z)(\frac{d^{2}w}{dxdy})(\frac{d{\varphi }_x}{dx})\\ +F{(}^Z\frac{d^2{\varphi }_x^2}{dxdy}+F{(}^Z\frac{d{\varphi }_x}{dx}.\frac{d{\varphi }_y}{dx}\end{array}$$ (57)

$$\begin{array}{l}{\epsilon }_y{}^2=Z^2{(}^{\frac{d^{2}w}{d{y}^2}}-2ZF(Z)(\frac{d^{2}w}{d{y}^2})(\frac{d{\varphi }_y}{dy})\\ +F{(}^Z{(}^{\frac{d{\varphi }_y}{dy}}\end{array}$$ (58)

$$\begin{array}{l}{\epsilon }_y{\gamma }_{xy}=2Z^2\frac{d^{2}w}{d{x}^2}.\frac{d^{2}w}{dxdy}-ZF(Z)(\frac{d^{2}w}{d{y}^2})(\frac{d{\varphi }_x}{dy})\\ -ZF(Z)(\frac{d^{2}w}{d{y}^2})\frac{d{\varphi }_y}{dx}-2ZF(Z)(\frac{d^{2}w}{dxdy})\frac{d{\varphi }_y}{dy}\\ +F{(}^Z(\frac{d^2{\varphi }_y^2}{dxdy})+F{(}^Z\frac{d{\varphi }_x}{dx}.\frac{d{\varphi }_y}{dx}\end{array}$$ (59)

$$\begin{array}{l}{\gamma }_{xy}^2=4Z^2{(}^{\frac{d^{2}w}{dxdy}}-4ZF(Z)(\frac{d^{2}w}{dxdy})(\frac{d{\varphi }_x}{dy})\\ -4ZF(Z)(\frac{d^{2}w}{dxdy})(\frac{d{\varphi }_y}{dx})+2F{(}^Z(\frac{d{\varphi }_x}{dy}).(\frac{d{\varphi }_y}{dx})\\ +F{(}^Z{(}^{\frac{d{\varphi }_x}{dy}}+F{(}^Z{(}^{\frac{d{\varphi }_y}{dx}}\end{array}$$ (60)

$${\gamma }_{xz}^2={\left(\frac{dF(Z)}{dz}\right)}^2{\varphi }_x^2$$ (61)

$${\gamma }_{xz}{\gamma }_{yz}={\left(\frac{dF(Z)}{dz}\right)}^2{\varphi }_x{\varphi }_y$$ (62)

$${\gamma }_{yz}^2={\left(\frac{dF(Z)}{dz}\right)}^2{\varphi }_y^2$$ (63)

Substituting equations (55) to (63) into equations (49) to (54) appropriately and then substituting the resultant equations into the total potential energy equation of (64) yielded equation (65) which is the total potential energy for a thick anisotropic plate of traditional third order shear deformation theory.

Total potential energy: The external work due to the uniform distributed normal (lateral) load shall be added to the obtained strain energy equation to obtain the total potential energy functional for rectangular thick anisotropic plate analysis as shown;

$$\Pi =U+V$$ (64a)

$$\begin{array}{l}\Pi =\frac{1}{2}{\int }_0^1{\int }_0^1{\int }_{-\frac{t}{z}}^{\frac{t}{z}}\left[\begin{array}{l}{\sigma }_x{\epsilon }_x+{\sigma }_y{\epsilon }_y+{\tau }_{xy}{\gamma }_{xy}+\\ {\tau }_{xz}{\gamma }_{xz}+{\tau }_{yz}{\gamma }_{yz}\end{array}\right]\\ -q{\int }_0^1{\int }_0^{1}wdxdy\end{array}$$ (64b)

$$\Pi =\frac{1}{2}{\int }_0^1{\int }_0^1[D_{11}\left\{\begin{array}{l}{\left(\frac{d^{2}w}{d{x}^2}\right)}^2-2g_2\left(\frac{d^{2}w}{d{x}^2}\right)\\ \left(\frac{d{\varphi }_x}{dx}\right)+g_3{\left(\frac{d{\varphi }_x}{dx}\right)}^2\end{array}\right\}$$

$$+D_{12}\left\{\begin{array}{l}{\left(\frac{d^{2}w}{dxdy}\right)}^2-g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_3\left(\frac{d{\varphi }_x}{dy}\right).{\left(\frac{d{\varphi }_y}{dx}\right)}^2\end{array}\right\}$$

$$+D_{13}\left\{\begin{array}{l}2\frac{d^{2}w}{d{x}^2}.\frac{d^{2}w}{dxdy}-3g_2\left(\frac{d^{2}w}{d{x}^2}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -g_2\left(\frac{d^{2}w}{d{x}^2}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_3\frac{d{\varphi }_x}{dx}.\frac{d{\varphi }_x}{dy}\\ +g_3\frac{d{\varphi }_x}{dx}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$+D_{21}\left\{\begin{array}{l}{\left(\frac{d^{2}w}{dxdy}\right)}^2-g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_3\left(\frac{d{\varphi }_x}{dy}\right).{\left(\frac{d{\varphi }_y}{dx}\right)}^2\end{array}\right\}$$

$$+D_{22}\left\{\begin{array}{l}{\left(\frac{d^{2}w}{d{y}^2}\right)}^2-2g_2\left(\frac{d^{2}w}{d{y}^2}\right)\\ \left(\frac{d{\varphi }_y}{dy}\right)+g_3{\left(\frac{d{\varphi }_y}{dy}\right)}^2\end{array}\right\}$$

$$+D_{23}\left\{\begin{array}{l}2\frac{d^{2}w}{d{y}^2}.\frac{d^{2}w}{dxdy}-g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -3g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_y}{dx}\right)\\ +g_3\frac{d{\varphi }_x}{dy}.\frac{d{\varphi }_y}{dy}+g_3\frac{d{\varphi }_y}{dy}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$+D_{31}\left\{\begin{array}{l}2\frac{d^{2}w}{d{x}^2}.\frac{d^{2}w}{dxdy}-3g_2\left(\frac{d^{2}w}{d{x}^2}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -g_2\left(\frac{d^{2}w}{d{x}^2}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_3\frac{d{\varphi }_x}{dx}.\frac{d{\varphi }_x}{dy}\\ +g_3\frac{d{\varphi }_x}{dx}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$+D_{32}\left\{\begin{array}{l}2\frac{d^{2}w}{d{y}^2}.\frac{d^{2}w}{dxdy}-g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -3g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_3\frac{d{\varphi }_x}{dy}.\frac{d{\varphi }_y}{dy}\\ +g_3\frac{d{\varphi }_y}{dy}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$+D_{33}\left\{\begin{array}{l}4{\left(\frac{d^{2}w}{dxdy}\right)}^2-4g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -4g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_y}{dx}\right)\\ +g_3{\left(\frac{d{\varphi }_x}{dy}\right)}^2+g_3{\left(\frac{d{\varphi }_y}{dx}\right)}^2+2g_3\frac{d{\varphi }_x}{dy}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$\begin{array}{l}+{\alpha }^2{g}_4{D}_{44}{\varphi }_x{}^2+{\alpha }^2{g}_4{D}_{45}{\varphi }_x{\varphi }_y\\ +{\alpha }^2{g}_4{D}_{45}{\varphi }_x{\varphi }_y+{\alpha }^2{g}_4{D}_{55}{\varphi }_y{}^2]dxdy\end{array}$$

$$-q{\int }_0^1{\int }_0^{1}wdxdy$$ (65)

Where:

$$g_1=\frac{{\int }_{-\frac{t}{z}}^{\frac{t}{z}}{z}^{2}dz}{\overline{D}}=\frac{t^3}{12\overline{D}}=1$$ (66)

$$g_2=\frac{\left({\int }_{-\frac{t}{z}}^{\frac{t}{z}}zF(z)dz\right)}{\overline{D}}$$ (67)

$$g_3=\frac{\left({\int }_{-\frac{t}{z}}^{\frac{t}{z}}F{(z)}^{2}dz\right)}{\overline{D}}$$ (68)

$${\alpha }^2{g}_4=\frac{\left({\int }_{-\frac{t}{z}}^{\frac{t}{z}}\left[\frac{dF{(z)}^2}{dz}\right]dz\right)}{\overline{D}}$$ (69)

The flexural rigidity of the plate is:

$$D=\frac{E}{1-{\mu }^2}*\overline{D}=\frac{E{t}^3}{12(1-{\mu }^2)}$$ (70)

The span-depth ratio is defined as:

$$\alpha =\frac{a}{t}$$ (71)

Also:

$$\begin{array}{l}{D}_{12}=D_{21};D_{31}=0.5D_{13};D_{32}\\ =0.5D_{23};D_{45}=D_{54}\end{array}$$ (72)

Substituting equation (72) into equation (65) gives:

$$\prod =\frac{1}{2}{\int }_0^1{\int }_0^1[D_{11}\left\{\begin{array}{l}{\left(\frac{d^{2}w}{d{x}^2}\right)}^2-2g_2\left(\frac{d^{2}w}{d{x}^2}\right)\\ \left(\frac{d{\varphi }_x}{dx}\right)+g_3{\left(\frac{d{\varphi }_x}{dx}\right)}^2\end{array}\right\}$$

$$+2D_{12}\left\{\begin{array}{l}{\left(\frac{d^{2}w}{dxdy}\right)}^2-g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ +g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_2\left(\frac{d{\varphi }_x}{dy}\right).\left(\frac{d{\varphi }_y}{dx}\right)\end{array}\right\}$$

$$+1.5D_{23}\left\{\begin{array}{l}2\frac{d^{2}w}{d{y}^2}.\frac{d^{2}w}{dxdy}-g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -3g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_3\frac{d{\varphi }_x}{dy}.\frac{d{\varphi }_y}{dy}+g_3\frac{d{\varphi }_y}{dy}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$+D_{22}\left\{\begin{array}{l}{\left(\frac{d^{2}w}{d{y}^2}\right)}^2-2g_2\left(\frac{d^{2}w}{d{y}^2}\right)\\ \left(\frac{d{\varphi }_y}{dy}\right)+g_3{\left(\frac{d{\varphi }_y}{dy}\right)}^2\end{array}\right\}$$

$$+1.5D_{23}\left\{\begin{array}{l}2\frac{d^{2}w}{d{y}^2}.\frac{d^{2}w}{dxdy}-g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_x}{dy}\right)\\ -3g_2\left(\frac{d^{2}w}{d{y}^2}\right)\left(\frac{d{\varphi }_y}{dx}\right)+g_3\frac{d{\varphi }_x}{dy}.\frac{d{\varphi }_y}{dy}+g_3\frac{d{\varphi }_y}{dy}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$+D_{33}\left\{\begin{array}{l}4{\left(\frac{d^{2}w}{dxdy}\right)}^2-4g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_x}{dy}\right)-4g_2\left(\frac{d^{2}w}{dxdy}\right)\left(\frac{d{\varphi }_y}{dx}\right)\\ +g_3{\left(\frac{d{\varphi }_x}{dy}\right)}^2+g_3{\left(\frac{d{\varphi }_y}{dx}\right)}^2+2g_3\frac{d{\varphi }_x}{dy}.\frac{d{\varphi }_y}{dx}\end{array}\right\}$$

$$\begin{array}{l}+{\alpha }^2{g}_4{D}_{44}{\varphi }_x{}^2+2{\alpha }^2{g}_4{D}_{45}{\varphi }_x{\varphi }_y\\ +{\alpha }^2{g}_4{D}_{55}{\varphi }_y{}^2]dxdy-q{\int }_0^1{\int }_0^{1}wdxdy\end{array}$$ (73)

This is a function that describes the shape of the normal to the mid-plane after deformation has taken place. In this thesis, a third order polynomial function will be employed to carry out a pure bending analysis of thick anisotropic rectangular plate of the various boundary conditions. The function is given as:

$$f(z)=z\left[1-\frac{4}{3}{\left(\frac{z}{t}\right)}^2\right]$$ (73a)

The function of equation (73a) can be derived from Shear stress across the thickness of a section of rectangular plates of Figure 1.

The maximum vertical shear stress equation across a rectangular section is given as:

$${\tau }_{\max }=\frac{VQ}{Ib}$$

Also, the first moment of area of a rectangular section is given as

$$Q={\displaystyle \int zdA}=\frac{b}{2}\left(\frac{t}{2}-Z\right)\left(\frac{t}{2}-Z\right)=\frac{b}{2}\left(\frac{t^2}{4}-Z^2\right)$$

Second moment of area of a rectangular section is commonly known as:

$$I=\frac{b{t}^2}{12}$$

Therefore;

$$\begin{array}{l}{\tau }_{\max }=6V\frac{\left(\frac{t^2}{4}-Z^2\right)}{b{t}^3}=\frac{3V}{2bt}\left(1-4\frac{z^2}{t^2}\right)\\ =\frac{v}{bt}G(Z)=G(Z)\tau \end{array}$$

Where the vertical shear stress profile G(Z) is given as;

$$G(Z)=\frac{3}{2}\left(1-4\frac{z^2}{t^2}\right)$$

From the above equations, nominal shear stress is given as;

$$\tau =\frac{V}{bt}$$

For traditional refined plate theory, it is assumed that the shear stress profile G(Z) is related to shear deformation profile, F(Z) as shown;

$$G(Z)=\frac{dF(Z)}{dZ}$$

Integrating G(Z) in the above equation with respect to Z gives the shear deformation parabolic profile as shown;

$$F(Z)=\frac{3}{2}Z\left(1-\frac{4}{3}{\left[\frac{z}{t}\right]}^2\right)$$

Ignoring the multiplier (1.5) we obtain cubic function shear deformation profile given as;

$$F(Z)=Z\left(1-\frac{4}{3}{\left[\frac{z}{t}\right]}^2\right)$$

Note that previous studies has shown that both functions, multiplier (1.5) or when ignored shall give the same result in thick plate analysis. Also, this shear deformation function was used by Murthy [28] in his work that was titled “Towards a consistent beam theory”. Sayyad [20] discussed other shear deformation profile equations used by other scholars. However, only the profile equation (73a) which was also used by Krishna Murty shall be used.

To obtain the equations of equilibrium of forces, the total potential energy functional shall be minimized by differentiating it with respect to the deflection, shear deformation rotation in x direction and shear deformation rotation in y direction (w, θsx and θsy) respectively as shown and these will yield the governing equation and two compatibility equations.

$$\frac{d\prod }{dw}=\frac{d\prod }{d{\varphi }_x}=\frac{d\prod }{d{\varphi }_y}=0$$ (74)

$$\begin{array}{l}\frac{d\prod }{dw}={\int }_0^1{\int }_0^1[D_{11}\left\{\frac{d^{4}W}{d{X}^4}-g_2\frac{d^3{\varphi }_x}{d{X}^3}\right\}+D_{12}\left\{2\frac{d^{4}W}{d{X}^{2}d{y}^2}-g_2\frac{d^3{\varphi }_x}{dXd{y}^2}-g_2\frac{d^3{\varphi }_y}{d{X}^{2}dy}\right\}\\ +0.75D_{13}\left\{4\frac{d^{4}W}{d{X}^{3}dy}-3g_2\frac{d^3{\varphi }_x}{d{X}^{2}dy}-g_2\frac{d^3{\varphi }_y}{d{X}^3}\right\}+D_{22}\left\{\frac{d^{4}W}{d{y}^4}-g_2\frac{d^3{\varphi }_y}{d{y}^3}\right\}\\ +0.75D_{23}\left\{4\frac{d^{4}W}{dXd{y}^3}-g_2\frac{d^3{\varphi }_x}{d{y}^3}-3g_2\frac{d^3{\varphi }_y}{dXd{y}^2}\right\}+D_{33}\left\{\frac{d^{4}W}{d{X}^{2}d{y}^2}-2g_2\frac{d^3{\varphi }_y}{d{X}^{2}dy}\right\}\\ -{\int }_0^1{\int }_0^{1}qdxdy=0\end{array}$$