Background: Research objective - to calculate energy of oscillation of biological time of plant in ontogenesis under the influence of weather environment. At the same time, the simplest model of system for the first calculation is taken.

Methods and Findings: Biological time is represented in the form of the dependence on photosynthesis and respiration processes of the whole plant organism via СО2 exchange. Two-dimensional temporal space is implemented naturally. Consideration is given to the issue of biological time oscillations during plant ontogenesis. It is believed that lowering the air temperature from the optimum level down to the actual temperature would deviate the biological temporal vector from the physical time axis. The time change is deemed to be an integral of the scalar product of the biological temporal vector with the physical time axis. The flow rate of biological time is determined by the rate of CO2 exchange for the whole plant depending on the state of environmental factors (photosynthetic active radiation (PAR), air temperature, and productive soil moisture). Oscillations of the newly obtained normalized logistic curve of plant growth are assigned to those of the whole plant biological time.

Conclusions: The potential and kinetic oscillation energy of biological time of the whole sunflower plant during ontogenesis is calculated subject to the condition of environmental factors. The plant organism is considered as a simplified system or a conservative system.

Development, Energy, Growth, Photosynthesis, Respiration, Time.

Background: Research objective - to calculate energy of oscillation of biological time of plant in ontogenesis under the influence of weather environment. At the same time, the simplest model of system for the first calculation is taken.

Methods and Findings: Biological time is represented in the form of the dependence on photosynthesis and respiration processes of the whole plant organism via СО2 exchange. Two-dimensional temporal space is implemented naturally. Consideration is given to the issue of biological time oscillations during plant ontogenesis. It is believed that lowering the air temperature from the optimum level down to the actual temperature would deviate the biological temporal vector from the physical time axis. The time change is deemed to be an integral of the scalar product of the biological temporal vector with the physical time axis. The flow rate of biological time is determined by the rate of CO2 exchange for the whole plant depending on the state of environmental factors (photosynthetic active radiation (PAR), air temperature, and productive soil moisture). Oscillations of the newly obtained normalized logistic curve of plant growth are assigned to those of the whole plant biological time.

Conclusions: The potential and kinetic oscillation energy of biological time of the whole sunflower plant during ontogenesis is calculated subject to the condition of environmental factors. The plant organism is considered as a simplified system or a conservative system.

Development, Energy, Growth, Photosynthesis, Respiration, Time.

We cannot see time, even with the strongest microscope. We can only study events and processes and compare time intervals to them. In this paper, we will study time with respect to the photosynthesis and respiration processes of plants, the plant growth processes, and the total dry plant biomass value.

It is known that the duration of plant ontogenesis is not a constant value relative to the physical (calendar) time axis. Thus, for example, the duration of sunflower ontogenesis in the south of Ukraine varies from 80 to 120 days. That is, biological time (simply, the time) tends to expand and compress depending on environmental factors [1-4].

The mathematical apparatus has been described in papers [5-7]. Let us briefly recall the principal points of the theory of oscillations. To begin with, we will consider the simplest oscillatory system described by the equation:

$$\frac{d^{2}x}{d{t}^2}=f(x)\left(1.1\right)$$

It is assumed that function f (x) is integrable and, generally, a nonlinear function of the x-coordinate. We will introduce a new variable: $y=\frac{dx}{dt}$ which allows us to exclude the time in an explicit form from the equations of motion, although, as before: x = x (t) and y = y (t). We can then state:

$$\frac{d^{2}x}{d{t}^2}=\frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}=\frac{dy}{dx}y\left(1.2\right)$$

In new coordinates, equation (1.1) takes the following form:

$$\frac{dy}{dx}=\frac{f(x)}{y}\left(1.3\right)$$

Having integrated equation (1.3), we obtain [5,7]:

$$\frac{1}{2}{y}^2-{\displaystyle \int f(x)dx}=h=const\left(1.4\right)$$

This is an expression for two types of energy. As is customary in physics, it speaks of kinetic energy and potential energy.

Let us consider the sum of the effective temperatures method (a method of degree-days). This method is based on the hypothesis that the sum of the effective temperatures necessary for a particular inter-phase development period to occur is constant. This hypothesis is expressed by the equation [4]:

$$n=\frac{A}{t_{sr}^o-B}\left(2.1\right)$$

where A - is a constant equal to the sum of the effective temperatures over the inter-phase development period, °С; t^o _sr is the average air temperature for the inter-phase development period, in °С; В is the lower limit of temperature for plant development, in °С; and n is the number of days in the inter-phase development period.

The moment of the plant development phase (the developmental phases for sunflowers are shoots, the second couple of real leaves, budding, blossoming, and full maturity of seed) is calculated using two equations. First, the effective temperature of the current day of calculation is to be computed:

$$\Delta t_d^o=t_d^o-B\left(2.2\right)$$

where t^оd is the average air temperature of the current day of calculation, in °С, and Δt_od is the effective temperature of the current day of calculation, in °С. Then, cumulatively, the sum of the effective temperatures for each day j of the inter-phase development period n is to be calculated:

$$t_s^o={\displaystyle \sum _{j=1}^n\Delta t_d^{oj}}0\le t^o{}_s\le A\left(2.3\right)$$

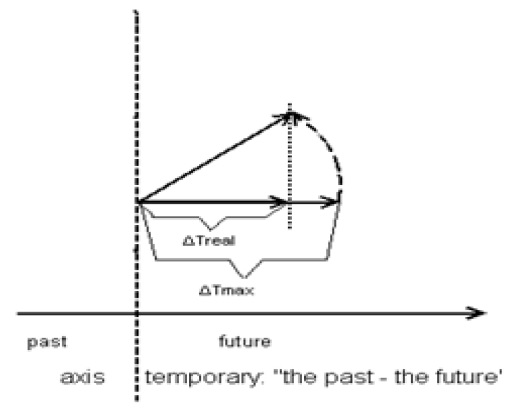
where j is the number of days of the development period and t^os is the sum of the effective temperatures for the interphase development period, in °С. Thus, the time under this method is measured in Celsius degrees instead of in true time units. To move toward real time, we will perform the following operation: by the time the sum of effective temperatures for the inter-phase development period tos has passed (this can also be one from “shoots” to “at full maturity of seed”), equal to A, it is considered that the development phase has occurred. We divide the right and the left sides of equation (2.3) by the sum of the effective temperatures equal to A, in °С. This means that we have normalized the sum of the effective temperatures. Now this sum is expressed by an analogue, which varies from 0 to 1 of the real time. The effective temperature of the current day of calculation, Δt^o _d, will also be expressed in relative units. This value corresponds to one day of physical (calendar) time. Thus, we have moved from the sum of effective temperatures method to the normalized real physical time. During the entire ontogenesis period, the time varies from some small t₀ up to 1 (from the “shoots” event to “at full maturity of seed”). The normalized physical time also depends on the average air temperature for the current day of calculation (equation (2.2)). Let us consider the elementary increment of the normalized real physical time for one day of calculation (2.2) under the sum of effective temperatures method. This increment of physical time depends on the average air temperature for the current day of calculation. Thus, if the air temperature is optimal (for example, 25 °С average air temperature of the settlement period for the sunflower), then the increment of the normalized physical time will be the largest, maximum ΔT_max= max. If the average air temperature for the current day of calculation dropped to a biological minimum temperature В = 10 °С (for sunflowers), then the increment of the normalized real physical time would be zero. That is, we can imagine that the temporal vector deviates from its normal position, the physical time axis. Such a physical time axis has a direction - from the past to the future. Then, the projection of this deviating vector onto the normal physical time axis will give a real time increment ΔT_real, Figure 1.

The ΔT_maxvalue represents the maximum increment of the temporal vector at the optimal average air temperature for the current day of calculation. When the average air temperature for the current day of calculation lowers, the temporal vector deviates. Thus, at the temperature of biological zero, or В temperature (equation (2.2)), the temporal vector ΔT_max will be orthogonal to the normal physical time axis, and the deviation angle α will equal π / 2, then the projected ΔT_max of the deviating temporal vector onto the normal physical time axis will be zero: ΔT_real= 0 (cos π/2 = 0), and development of the plant (sunflower) will be suspended. Thus, the angle α of deviation of the real temporal vector depends on the average air temperature of the current day of calculation. That is, with equation (2.2), we calculate the scalar product of the deviation of the temporal vector ΔT_max from the physical time axis. From this, it can be seen that with the sum of effective temperatures method, we can calculate the sum of the scalar products of the deviation of the real temporal vector ΔT_max from the physical time axis. Moving to the limit when the increment ΔTmax tends toward zero, we obtain the integral of the scalar product (Budak B.M., Fomin S.V. 1967). In this case, the line (2.3) turns into a curve in some two-dimensional temporal space, Figure 1, (Naumov M.M. 2004, 2005) [8.9]. Thus, we obtain a curvilinear integral:

$$T={\displaystyle \underset{{\tau }_b,{\tau }_e}{\int }(F,d\tau )}\left(2.4\right)$$

where T is the value of the real normalized biological time, in relative units; (F, dτ) is the scalar product of the deviation of the real biological temporal vector from the physical time axis; dτ is the vector ΔT_max when it tends toward infinitesimal; F is the deviating vector ΔT_max at the angle α when the average daily air temperature lowers from the optimal temperature to the real one; and τb and τe are the starting point (“shoots”) and the end point (“at full maturity of seed”) of the biological time curve, respectively.

$$T(t)={\displaystyle {\int }_{t_b}^{t_e}\left[P(t)\frac{d\varphi (t)}{dt}+Q(t)\frac{d\psi (t)}{dt}\right]}dt, t_0\le t\le 1.\left(2.5\right)$$

Here, P (t) and Q (t) are some functions to be defined later on and t is the physical time axis, in relative units, where for the entire ontogenesis (from the “shoots” event to the “at full maturity of seed” event), the time t varies from some small t₀ (corresponding to the “shoots” event: let i be, for example, t₀ = 0.01) to 1 (“at full maturity of seed” event). Let us differentiate this already calculated integral (2.5) with respect to t. We obtain:

$$\frac{dT(t)}{dt}=P(t)\frac{d\varphi (t)}{dt}+Q(t)\frac{d\psi (t)}{dt},t_0\le t\le 1.\left(2.6\right)$$

Now we write down the equation (Davidson J.L., Philip J.R. 1958), which shows that the incremental change of the dry biomass of the whole plant depends on its CO₂ exchange:

$$\frac{dM(t)}{dt}=\frac{dФ(t)}{dt}-\frac{dR(t)}{dt},t_0\le t\le 1.\left(2.7\right)$$

where M (t) is the total dry plant biomass value, g ∙ plant-1; $\frac{dФ(t)}{dt}$ is the photosynthesis rate of the whole plant in ontogenesis, g ∙plant^-1 ∙day^-1; and $\frac{dR(t)}{dt}$ is the respiration rate of the whole plant in ontogenesis, g ∙ plant^-1∙day^-1. Let us write down the equation (2.7) in another form:

$$dM(t)=\left(\frac{dФ(t)}{dt}-\frac{dR(t)}{dt}\right)dt, t_0\le t\le 1,\left(2.8\right)$$

and represent the total dry plant biomass value M (t) in the normalized form. It is known that accumulation of the total dry biomass of the whole plant is subject to the S-shaped growth pattern [10]. Now we take the value of the final total dry biomass of the whole plant and divide it by the current value of the total dry plat biomass. Then, we obtain that the total dry biomass of the whole plant will vary in relative units: from small M₀ corresponding to the shoots event to 1 corresponding the at full maturity of seed event. The S-shaped growth will be maintained and at the end of ontogenesis, for the “at full maturity of seed” event, the total dry plant biomass will equal μ = 1. Now we replace M (t) with the normalized values of the total dry plant biomass μ (t) in equation (2.8). We obtain:

$$d\mu (t)=\left(\frac{d{Ф}_{\mu }(t)}{dt}-\frac{d{R}_{\mu }(t)}{dt}\right)dt,t_0\le t\le 1,\left(2.9\right)$$

where Ф_μ(t) is the photosynthesis output value of the whole plant during ontogenesis, which depends on the physical time t, in relative units and Rμ(t) is the respiration output value of the whole plant during ontogenesis, which depends on the physical time t, in relative units. We write down equation (2.6) in the same form and compare it with equation (2.9):

$$dT(t)=\left(P(t)\frac{d\varphi (t)}{dt}+Q(t)\frac{d\psi (t)}{dt}\right)dt,t_0\le t\le 1,\left(2.10\right)$$

Plant age is determined by the growth and development of the entire organism. That is, plant age is determined by the total dry biomass value, comprising the development of its individual organs and systems (leaves, roots, stems, reproductive organs, conducting systems, xylems, phloem, etc.). Thus, if, for example, the value of the normalized total dry biomass of the whole plant is μ (t) = 0.3, then the real biological time of ontogenesis is equal to 0.3 relative units of biological time, too. In this case, we will assume that the biological time corresponds exactly to the normalized value of the total dry plant biomass μ (t). From this, we obtain that the functions in equation (2.10) match exactly the photosynthesis and respiration rates of the whole plant:

$$P(t)\frac{d\varphi (t)}{dt}=\frac{d{Ф}_{\mu }(t)}{dt},t_0\le t\le 1,\left(2.11\right)$$

$$Q(t)\frac{d\psi (t)}{dt}=-\frac{d{R}_{\mu }(t)}{dt},t_0\le t\le 1.\left(2.12\right)$$

Hence, change of biological time is entirely dependable on the processes of photosynthesis and respiration of the plant, meaning on the СО₂ exchange of the whole organism. Because the photosynthesis and respiration rates depend on the culture genotype and environmental factors (temperature, productive soil moisture, light, mineral nutrition and other factors), then the biological time will depend on these factors, too:

$$\frac{dT(t)}{dt}=\frac{d{Ф}_{\mu }(t)}{dt}-\frac{d{R}_{\mu }(t)}{dt},t_0\le t\le 1.\left(2.13\right)$$

Now let us consider equation (2.9) which shows the incremental change of the total dry biomass in normalized form with respect to the normalized time, where during the entire ontogenesis the normalized physical time t varies from some small t₀ to 1:

$$\mu (t)={\displaystyle \underset{t_0}{\overset{1}{\int }}\left(\frac{d{Ф}_{\mu }(t)}{dt}-\frac{d{R}_{\mu }(t)}{dt}\right)dt}={\displaystyle \underset{t_0}{\overset{1}{\int }}\frac{d\mu (t)}{dt}dt}={\displaystyle \underset{t_0}{\overset{1}{\int }}d\mu (t)}\left(2.14\right)$$

Here, the total СО2 exchange in the plant determines the increments and growth of the normalized total dry biomass, where t₀ is the moment of growth beginning, and 1 is the moment of growth completion, that is, from the shoots event to the at full maturity of seed event.

For further calculation of the total kinetic and potential energy of the whole plant organism, we need a logistic growth curve for the total dry plant biomass in normalized form. We have also obtained that it is removed by means of a theory of oscillation, as verified in preceding papers (Naumov M.M. 2004, 2005, 2010, 2011) [8,9,11,12] which has the following form:

$$\mu (t)=-\frac{1}{{\omega }_0}\sin ({\omega }_{0}t+{\beta }_0)+t,t_0\le t\le 1,\left(2.15\right)$$

where ω₀ is the cyclic oscillation frequency equal to ${\omega }_0=\frac{2\pi }{T_0}$ [5], in which T0 is an oscillation period equal to the whole ontogenesis, starting from the shoots event until the at full maturity of seed event, T₀ = 1; and β₀ is the initial phase of development of oscillations of the normalized physical plant time (let us assume that for the growth state, for the shoots event, the initial phase of development of oscillations is equal to β₀= 0.01 radian). The first derivative of the normalized logistic growth curve of the total dry biomass of the whole plant with respect to the physical time t is as follows:

$$\frac{d\mu (t)}{dt}=-\cos ({\omega }_{0}t+{\beta }_0)+1,t_0\le t\le 1,\left(2.16\right)$$

This equation shows the change in the growth rate of the normalized total dry biomass of the whole plant and depends entirely on the current state of the environmental factors such as PAR, heat, productive soil moisture, nutrition, СО₂ content in the air and other unconsidered factors. It should be mentioned that some of the factors influencing the growth processes of the normalized total dry biomass of the whole plant in equation (2.16) have not been considered yet.

The second derivative of the normalized logistic growth curve of the total dry biomass of the whole plant with respect to the physical time t is as follows:

$$\frac{d^2\mu (t)}{d{t}^2}={\omega }_0\sin ({\omega }_{0}t+{\beta }_0),t_0\le t\le 1.\left(2.17\right)$$

Here, as well, we have not considered the effects of environmental factors on the second derivative of the normalized growth rate of the logistic curve.

Thus, taking into account equations (2.9), (2.13), and (2.14), the biological time oscillations T in plant ontogenesis, having excluded the effect of the environmental factors, would be presented as follows:

$$T(t)=-\frac{1}{{\omega }_0}\sin ({\omega }_{0}t+{\beta }_0)+t,t_0\le t\le 1,\left(2.18\right)$$

$$\frac{dT(t)}{dt}=-\cos ({\omega }_{0}t+{\beta }_0)+1,t_0\le t\le 1,\left(2.19\right)$$

$$\frac{d^{2}T(t)}{d{t}^2}={\omega }_0\sin ({\omega }_{0}t+{\beta }_0),t_0\le t\le 1.\left(2.20\right)$$

Thus, equations (2.18) (2.19), and (2.20) describe the biological time oscillations of the whole organism, regardless of the current condition of environmental factors in the normalized form. These equations describe the genetic features of plants in relative time units, where during the entire ontogenesis, the physical time t varies from some small value (for the shoots event) t₀ to 1 (for the at full maturity of seed event).

Now we can compute the kinetic and potential energy of biological time oscillations T in plant ontogenesis in relative units with equation (1.4).

The kinetic energy K(t) of the biological time oscillations of the whole plant organism, regardless of the environmental factors in the normalized form, is as follows:

$$K(t)=\frac{1}{2}{y}^2=\frac{1}{2}{\left(-\cos ({\omega }_{0}t+{\beta }_0)+1\right)}^2,t_0\le t\le 1.\left(2.21\right)$$

Having the brackets removed and similar terms collected, we obtain the following equation for the kinetic energy of the biological time T oscillations of the whole plant, regardless of the current condition of environmental factors:

$$K(t)=\frac{1}{4}\cos \left(2{\omega }_{0}t+2{\beta }_0\right)-\cos \left({\omega }_{0}t+{\beta }_0\right)+\frac{3}{4},t_0\le t\le 1.\left(2.22\right)$$

The equation of the kinetic energy of biological time oscillations of the whole plant (2.22) has three terms: the first two are dynamic, ontogenesis time-dependent and responsible for addition of two harmonic oscillations of biological time in ontogenesis, and the third one is a constant responsible for positive values of kinetic energy. The constant of kinetic energy i should say that the vital processes permanently occur.

The potential energy V(t) of the biological time oscillations of the whole plant, regardless of the environmental factors in the normalized form, is as follows:

$$V(t)=-{\displaystyle \int f(x)dx=}-{\displaystyle \underset{}{\overset{}{\int }}{\omega }_0\sin \left({\omega }_{0}t+{\beta }_0\right)\cdot \left(-\cos ({\omega }_{0}t+{\beta }_0)+1\right)dt},t_0\le t\le 1.\left(2.23\right)$$

We have recorded the potential energy directly for the physical time variable t, as equation (2.19):

$$dT(t)=\left(-\cos ({\omega }_{0}t+{\beta }_0)+1\right)dt$$

By integrating this equation, we obtain a dependence of the change in the potential energy of the biological time oscillations of the whole plant in ontogenesis, regardless of the current condition of environmental factors:

$$V(t)=-\frac{1}{4}\cos \left(2{\omega }_{0}t+2{\beta }_0\right)+\cos \left({\omega }_{0}t+{\beta }_0\right)+C_V,t_0\le t\le 1.\left(2.24\right)$$

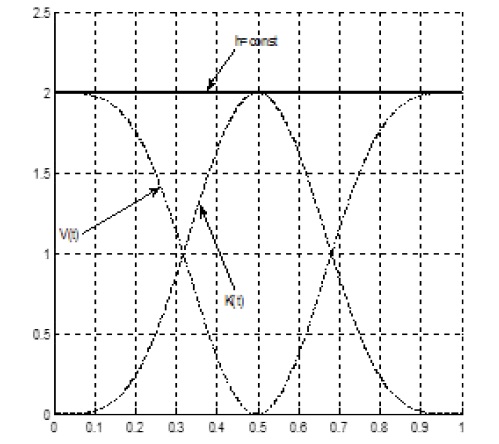
where C_V is the constant of integration, a constant of potential energy of the biological time oscillations. The constant value of potential energy CV shall be such that the potential energy V (t) is always positive and equal to zero in the minimum point. Such a constant was found by the potential energy curve fitting method with calculations on PC in the MATLAB system. Then, the constant of integration of the potential energy of the biological time oscillations of the whole plant, regardless of the current condition of environmental factors is C_V= 5/4. Now, we can figure the kinetic and potential energy of the biological time oscillations of the whole plant, regardless of the current condition of environmental factors in relative units during ontogenesis, Figure 2.

As seen at Figure 2, the kinetic energy of the biological time oscillations of the whole organism at the beginning and the end of growth takes a zero value. Halfway through the plant growth, at the middle point of ontogenesis t = 0.5, the kinetic energy of the biological time oscillations takes the maximum value K (t) = max. The potential energy V (t) at the beginning and at the end of growth has a maximum value. The potential energy of the biological time oscillations at the end of ontogenesis, at the at full maturity of seed event, is fully stored in the reproductive organs, the plant seeds (in sunflower seeds). Similarly, we can note that the potential energy of the biological time oscillations at the beginning of growth, at the sowing event, is entirely contained in the plant (sunflower) seeds, and for the shoots event, it has some lower value, as potential energy has been spent on the growth and development of the plant organism.

The total energy of the biological time oscillations of the whole plant in accordance with the energy conservation law for a conservative system always remains constant: h = K (t) + V (t) = const. Now let us examine the change in the kinetic and potential energy of the biological time oscillations of the whole plant under real ontogenesis. To do this, we take the sunflower that used to grow in the real conditions of the Odessa region, Chernomorka village in 1986.

Example of calculating the potential and kinetic energy of biological time oscillations of the whole sunflower plant in a real environment in 1986.

For the calculation, we will follow the following pattern. First, we calculate the tension level of environmental factors (PAR, heat, productive soil moisture) for every day of ontogenesis. To do this, we take the average decade data and assume that during the given calculation decade of growth and development of the sunflower, the values of PAR, average daily air temperature, and productive moisture reserves within a 1-meter-deep soil layer were at the same level. We assume that the level of soil nutrition was optimal. The CO₂ content in the air corresponds to the normal level.

Then, we calculate the change in the normalized physical time t with respect to the calendar time j. Next, we calculate the growth rate of the total dry biomass of the whole sunflower plant in real environmental conditions, taking into account the current environmental factors. Then, we calculate the real dynamics of the total dry sunflower plant biomass during ontogenesis and compare it with the measured values of the total dry biomass in 1986. Further, we will require the final calculated value of the total dry sunflower plant biomass. Then, we will normalize the growth rate of the total dry sunflower plant biomass to obtain the normalized values of the plant biological time T. Finally, we calculate the kinetic and potential energy of the biological time oscillations of the sunflower plant under the real environmental conditions of 1986.

Let us calculate the tension level of environmental factors. To integrate, we need to choose the integration interval. The integration interval for us cannot be less than one day. It is known that there are daily dynamics of photosynthesis and respiration of plants, and these photosynthesis and respiration dynamics are not considered in our calculations for the time being. We will compute the average change in photosynthesis and respiration for the given calculated day. Therefore, for our calculations, we have chosen the integration interval to be one day. The level of tension of the environmental factors U_ee(j) is thus calculated by the equations:

Light (Gulyaev BI, 1983) [13]

$${\chi }_{light}(j)=1-\exp \left(-C_i\cdot I_{opt}\cdot I_S(j)\right)\left(3.1\right)$$

Heat (Horie T, 1977) [14]

$${\lambda }_{warmly}(j)=1-a_t{(t_{opt})}^2{\left(t_r^o(j)-1\right)}^2\left(3.2\right)$$

Soil moisture (Polevoy AN, 1983) [15]

$${\gamma }_{moisture}(j)=1-a_w{(W_{opt})}^2{\left(W_S(j)-1\right)}^2\left(3.3\right)$$

where j is the day number in ontogenesis (from the shoots event to the at full maturity of seed event), in calendar time; χ_light(j) is the exponential normalized light curve for the photosynthesis rate of sunflower culture, in relative units; I_opt is the optimal PAR flow at the upper sunflower sowing limit for the growth and photosynthesis processes to run at maximum rate, I_opt= 650 W·m^-2; I_S(j) is the normalized real PAR flow at the upper sowing limit, in relative units; C_i is the light curve parameter which, along with value I_opt, determines the degree of the light curve inflection, Ci=0.01 m^-2·W^-1; λ_warmly(j) is the normalized temperature curve parabola for the growth and photosynthesis of sunflower culture, in relative units; to opt is the optimal average daily air temperature for the growth and photosynthesis processes of sunflower culture, t^o _opt=25 °С; t^o _r(j) is the normalized real average daily air temperature within the sowing period, in relative units; a_t is the temperature curve parameter which, along with value t_opt, determines the critical points for the growth and photosynthesis processes of sunflower culture to occur, a_t =0.0022 °^С-2; γ_moisture(j) is the normalized moisture curve parabola for the growth and photosynthesis of sunflower culture, in relative units; Wopt is the optimal reserve of productive moisture within a 1 meter-deep soil layer for the processes of growth and photosynthesis to occur, which for the Odessa region, Chernomorka village is W_opt = 131.9 mm; W_S(j) is the normalized real reserve of productive moisture within a 1 meter-deep soil layer, in relative units; and a_w is a parameter of the moisture curve for the growth and photosynthesis of sunflower culture which, along with value W_opt, determines the critical points for the photosynthesis process to occur, a_w =0.00004 mm^-2.

To calculate the PAR flow at the upper sunflower sowing limit equation is used:

$$I_{PAR}(j)=\left[12.66\cdot S{S}^{1.31}(j)+315{(a+b)}^{2.1}\right]\cdot \frac{41868}{3600{\tau }_{day}(j)}\left(3.4\right)$$

where I_PAR(j) is the PAR flow at the upper sowing limit, W·m^-2; SS (j) is the duration of sunshine hours per day, in hrs; (a + b)=sinh₀(j), where: h₀(j) is the Sun’s midday height; and τ_day(j) is the length of daylight hours, in hrs.

We only have to compute the normalized values of the PAR flow, the average daily air temperature and the reserves of productive moisture within a 1-meter-deep soil layer:

$$I_S(j)=\frac{I_{PAR}(j)}{I_{opt}};\left(3.5\right)$$

$$t_r^o(j)=\frac{t_{air}(j)}{t_{opt}};\left(3.6\right)$$

$$W_S(j)=\frac{W_{stocks}(j)}{W_{opt}};\left(3.7\right)$$

where t_air(j) is the current average daily air temperature, in °С and W_stocks(j) is the current reserve of productive moisture within a 1-meter-deep soil layer, in mm.

Finally, the level of tension of the environmental factors U_ee(j) can be calculated with Liebig-Blackman’s principle, which considers the impact of each factor on the growth and photosynthesis rates for sunflower culture for every day of ontogenesis:

$$U_{ee}(j)={\chi }_{light}(j)\cdot {\lambda }_{warmly}(j)\cdot {\gamma }_{moisture}(j)\left(3.8\right)$$

Now, we should calculate the normalized physical time axis t with respect to the calendar time. Calculation of this normalized time will be based on the formulas [16,17]:

$$t(j+1)=t_0+t(j)+U_{ee}(j)\cdot \Delta t_{opt},t_0\le t\left(j\right)\le 0.5\left(3.9\right)$$

$$t(j+1)=t(j)+\frac{\Delta t_{opt}}{U_{ee}(j)},0.5\le t\left(j\right)\le 1.\left(3.10\right)$$

where j is the day number in ontogenesis from the shoots event to the at full maturity of seed event; t₀ is the initial value of the normalized physical time axis (for the shoots event), in relative units: t₀= 0.01; t (j) is the normalized value of the physical time axis, which depends on the day number in ontogenesis j, in relative units: t₀ ≤ t ≤ 1; Δt_opt is a constant related to the maximum development rate for optimal values of environmental factors, for sunflowers: Δt_opt= 0.0097 relative physical normalized time units ∙ day^-1. To calculate the optimal rate of the plant development, Δt_opt (sunflower), it is necessary to take the average long-term value for the duration of the shoots-to-at full maturity of seed period of development. For example, let us assume the duration of this period of development to be 103 days. Then, the value Δt_opt will be calculated from Δt_opt= 1/103 = 0.0097 relative units of the normalized physical time per day. Equations for calculating the normalized physical time axis t were obtained and verified in literature [16,17]. According to those studies, the moment when the relative time axis t (j) is equal to 0.5 corresponds to the blossoming event of the sunflower.

Now, we will calculate the dynamics of the real growth rate of the total dry biomass of the sunflower plant, taking into account the influencing environmental factors (PAR, average daily air temperature, productive soil moisture), because the process of the growth rate of the total dry biomass is affected by current environmental factors, shown in equation (2.8), which shows that the growth rate of the plant is completely dependent on environmental factors through the processes of photosynthesis and respiration of the culture [11,12]:

$$M_{real}(j+1)=M_{real}(j)+U_{ee}(j)\frac{\Delta M_{\max }}{\Delta t}\left(-\cos ({\omega }_{0}t(j)+{\beta }_0)+1\right),\left(3.11\right)$$

where M_real(j) is the real total dry biomass of the whole sunflower plant, g ∙ plant^-1 and $\frac{\Delta M_{\max }}{\Delta t}$ is the maximum growth rate of the total dry biomass of the whole sunflower plant for one day of calendar time j in optimal environmental conditions, here Δt = 1 day, g∙plant^-1∙day^-1. The maximum growth rate is observed in the middle of ontogenesis and is equal to $$\frac{\Delta M_{\max }}{\Delta t}$$ =12.1 g∙plant^-1∙day^-1 (this value was obtained by the author as a result of experimental observations of sunflower sowing in the village of Chernomorka in 1986 and numerical experiments on a PC in the MATLAB system). Integrating equation (3.11) for every current day of calculation, from the shoots event to the at full maturity of seed event, we obtain the value of the final total dry biomass of the whole sunflower plant, which amounts to the value M_final = 924.6 g ∙ plant^-1, Figure 3.

Now we can normalize equation (3.11) by the value of the final total dry biomass of the whole sunflower plant organism M_final:

$$\mu (j+1)=\mu (j)+U_{ee}(j)\frac{\Delta M_{\max }}{\Delta t\cdot M_{final}}\left(-\cos ({\omega }_{0}t(j)+{\beta }_0)+1\right).\left(3.12\right)$$

Such normalization will allow calculation of the kinetic energy of the biological time oscillations of the whole sunflower plant in the real growing conditions in 1986 with equation (3.14), see equations (2.21) and (2.22). Let us denote the variable G (j):

$$G(j)=U_{ee}(j)\frac{\Delta M_{\max }}{\Delta t\cdot M_{final}}.\left(3.13\right)$$

Then, the kinetic energy of the biological time oscillations of the whole sunflower plant organism K (j) will equal:

$$K(j)=\frac{1}{4}{\left(G(j)\right)}^2\cos \left(2{\omega }_{0}t(j)+2{\beta }_0\right)-{\left(G(j)\right)}^2\cos \left({\omega }_{0}t(j)+{\beta }_0\right)+{\left(G(j)\right)}^2\frac{3}{4}.\left(3.14\right)$$

The plot of the obtained kinetic energy of biological time oscillations of the sunflower plant grown in 1986 in the Odessa region, Chernomorka village is presented at Figure 4.

The potential energy of the biological time oscillations of the sunflower plant organism V (j) is calculated from the fact that the total energy is always constant for a conservative system: h = K (t) + V (t) = const and that there is a maximum value for the kinetic energy in ontogenesis (Figure 2). Then, the potential energy of the biological time oscillations of the sunflower plant can be calculated from the fact that we assume the sunflower plant to be a conservative system in the first approximation. This means that the total energy h is always constant, even under the real environmental conditions, although these environmental factors vary very dynamically. Let us consider, however, that h = const (1986). Thus, since at the middle time point of ontogenesis, the value of kinetic energy of the plant biological time oscillations reaches its maximum value, while at the same moment of ontogenesis the potential energy of the plant biological time oscillations equals zero (Figure 2), then we can calculate the potential energy with the equation:

$$V(j)=K_{\max }(1986)-K(j),\left(3.15\right)$$

where K_max (1986) is the maximum value of the kinetic energy under the growing conditions of sunflower culture in 1986 in the Chernomorka village, which is K_max(1986) =2.0092∙10^-4 day^-2. The plot of the obtained potential energy of biological time oscillations of sunflower plant organism is shown in Figure 4. According to our data on sunflower growing in 1986, the blossoming event for sunflowers occurred on the 63rd day from the shoots event, which corresponds to the maximum kinetic energy of the biological time oscillations of the sunflower plant in ontogenesis. The same blossoming event for the sunflower corresponds to the minimum potential energy of the biological time oscillations of the sunflower plant.

We started this study with the analysis of the sum of effective temperatures method (degree-days) and came to the conclusion that the rate of plant development depends on the processes of photosynthesis and respiration of the culture, or on the CO₂ exchange of the whole plant. At the same time, one can consider abstract intervals of time, not just the sum of effective temperatures method. If we assume that the time inside the plant expands and compresses linearly depending on the environmental factors, we will obtain the same conclusions based on the fact that the temporal vector rotates around the point of the current moment of ontogenesis. We calculated the projection of the deviating temporal vector onto the physical time axis. As a result, the biological time was calculated using the integration of the scalar product of two temporal vectors. This means that we obtained the meaning of work in the physical sense of the word, which produces time.

It is known that the rate of plant development is determined by the factors of heat, productive soil moisture, light, and plant nutrition. In our case, we have obtained that the rate of change of the biological time T is entirely determined by the total CO2 exchange of the culture, which in turn is determined by the factors of light, heat, productive soil moisture, nutrition and other unconsidered factors. For example, changing the content of CO₂ in the air affects the rate of development.

It should be noted that the study gave the equation of harmonic oscillations of the biological time T(t) as:

$$\frac{d^{2}T(t)}{d{t}^2}+{\omega }_0^{2}T(t)={\omega }_0^{2}t$$

This equation can be regarded as the effect of the driving force of physical time t on the harmonic oscillations of biological time T(t). At the same time, it is known that the processes of photosynthesis and respiration of a plant, first of all, depend on incoming light waves (PAR). Therefore, the equation of the harmonic oscillations of biological time must be matched to the oscillations of light waves.

Also note that this equation of the harmonic oscillations of biological time has been established for the whole organism of the plant. On the other hand, the plant consists of growing organs—leaves, stems, roots, and reproductive organs. The growth of these organs is also described by the obtained logistic growth curve in the normalized form (2.15). Thus, the biological time of the organ will also be described by the equation of the harmonic oscillations of biological time, up to the cells. Studies of isotopic monitoring of cell metabolism show that carbon metabolism in the photosynthetic cell is an oscillatory process [18]. However, this is the material of another study.`