Journal Name: J Clinical Pharmacy
Article Type: Review
Received date: 25 May, 2019
Accepted date: 12 June, 2019
Published date: 21 June, 2019
Citation: Micha?owski T, Micha?owska-Kaczmarczyk AM, (2019) General Properties of the Balance 2 f(o)-f(h) in Electrolytic systems. Some Detailed Remarks on Elemental versus Core Balances. J Clin Pharm Vol: 1, Issu: 1 (05-16).
Copyright: © 2019 Micha?owski T. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Any electrolytic system in aqueous media is described with use of charge balance, f0 = ChB, and K elemental or core balances, fk = f(Yk) (k = 1,…,K). The balances: f1 = f(H) and f2 = f(O) are the basis to formulate the linear combination f12 = 2f2 – f1 = 2f(O) - f(H). For a redox system with K–K* electron-active elements (players), f12 is linearly independent on f0, f3,…, fK, i.e., the redox system is described by K independent balances f0, f12, f3,…, fK. For a non-redox system (K*=K), f12 is linearly dependent on f0, f3,…, fK, i.e., a redox system is described by K–1 independent balances f0,f3,…,fK. Consequently, the linear combination
with dk equal to the oxidation numbers of the related elements, is reducible to identity, 0=0, for a non-redox system, i.e., f12 is not the independent balance in this system. In a redox system, f12 is the primary form of Generalized Electron Balance (GEB). The paper is completed by description of typical redox and non-redox systems according to GATES/GEB principles.
Keywords
Electrolytic redox systems, GATES/GEB, Approach I to GEB, Approach II to GEB, Potentiometric titration.
Abstract
Any electrolytic system in aqueous media is described with use of charge balance, f0 = ChB, and K elemental or core balances, fk = f(Yk) (k = 1,…,K). The balances: f1 = f(H) and f2 = f(O) are the basis to formulate the linear combination f12 = 2f2 – f1 = 2f(O) - f(H). For a redox system with K–K* electron-active elements (players), f12 is linearly independent on f0, f3,…, fK, i.e., the redox system is described by K independent balances f0, f12, f3,…, fK. For a non-redox system (K*=K), f12 is linearly dependent on f0, f3,…, fK, i.e., a redox system is described by K–1 independent balances f0,f3,…,fK. Consequently, the linear combination
with dk equal to the oxidation numbers of the related elements, is reducible to identity, 0=0, for a non-redox system, i.e., f12 is not the independent balance in this system. In a redox system, f12 is the primary form of Generalized Electron Balance (GEB). The paper is completed by description of typical redox and non-redox systems according to GATES/GEB principles.
Keywords
Electrolytic redox systems, GATES/GEB, Approach I to GEB, Approach II to GEB, Potentiometric titration.
Introduction
The article concerns fundamental regularities, obligatory for electrolytic systems of different complexity, considered from the viewpoint of Generalized Approach to Electrolytic Systems (GATES), formulated by Michałowski (1992) [1,2]. According to GATES, a balancing of any electrolytic system is based on rules of conservation of particular elements, and on a charge balance, expressing the rule of electro-neutrality of this system. We refer to aqueous media, W=H2O, where the species exist as hydrates ± 1, ± 2,…is a charge, expressed in elementary charge units, e = F/NA (F = Faraday’s constant, NA = Avogadro’s number, ni = niW = niH2O ≥ 0 is a mean number of water (W=H2O) molecules attached to For ordering purposes, we assume Y1 = H (hydrogen) and Y2 = O (oxygen), and formulate first the linear combination
(1)
of elemental balances: f1 = f(H) for hydrogen (H) and f2 = f(O) for oxygen (O), related to the system considered. Then the linear combination of f12 with charge balance (f0,) and elemental/core balances fk = f(Yk) (k=3,…,K) for elements/cores Yk ≠ H, O will be formulated [3]. A core is considered as a cluster of different atoms with defined composition (expressed by chemical formula), structure and external charge, e.g. SO4-2 is a core with external charge –2, composed of two elements: S and O. The balances fk (k=1,…,K) interrelate the numbers of different elements/ cores in components forming a system, and in the species thus formed. The notation of the balances (f0, f1, …, fK) applied here is as follows
(2)
where {cjk}is referred to a set of some components, {sjk}- to some species in k-th balance; {ci0}=0, i.e., (empty set, for f0). Numbers of components of j-th kind are denoted by N0j (j=1,…,J), numbers of the species of i-th kind are denoted by Ni (i=1,…,I). For balancing purposes, the hydrated species in the system are specified as (Ni, ni); e.g., the notation HSO4-1 (N5, n5) applied in Example 1 (below) refers to N5 ions of HSO4-1∙n5H2O involving: N5(1+2n5) atoms of H, N5(4+n5) atoms of O, and N5 atoms of S. Molar concentration of the species be denoted by
The f12 (Equation 1) is the primary form of Generalized Electron Balance (GEB), f12 = pr-GEB, formulated (2005) for redox systems according to Approach II to GEB, where prior knowledge of ONs of all elements in components and species is not needed. The Approach II to GEB is fully compatible with the Approach I to GEB [4-15] formulated (1992) and based on the principle of common pool of electrons involved with electron-active elements, named as ‘players’ and distinguished from electron-non-active elements considered as ‘fans’, when a redox system is considered according to card game principle [15]; ONs for elements in components and species are needed in the Approach I. The principles of GEB formulation, discovered (1992, 2005) by Michałowski and resolved according to Generalized Approach to Electrolytic Systems (GATES) as GATES/GEB [1,16], were unknown in earlier literature.
GEB completes the set of K balances (f0, f12, f3,…, fK) as algebraic equations necessary for solving a redox system; K-1 balances (f0, f3,…, fK) are required for solving a non-redox system; f12 is omitted as derivative (not primary) balance. GEB is the law of Nature related to equilibrium, metastable or kinetic electrolytic redox systems, of any degree of complexity [1,15-24].
In this paper, the general properties of the linear combination of the balances (f0, f12, f3,…, fK) related to nonredox and redox systems of different degree of complexity, are discussed. Any redox system is involved with change of oxidation numbers of K-K* electron-active elements (players), where K* is the number of electron-non-active elements (fans). For a non-redox system, we have K*=K, i.e., K – K* = 0. Assuming that H and O participate the system as fans, we formulate the linear combination [15,16,25-33].
(3)
applicable for non-redox and redox systems, of different degree of complexity. For a non-redox system
(3a)
is transformed into identity, 0 = 0. We prove that the equation (3)
(1o) implies a general criterion distinguishing between non-redox and redox systems;
(2o) defines dk as oxidation numbers (ONs) of particular elements in components and species of a non-redox or redox system.
Synthesis of chemical and physical laws of conservation is expressed, respectively, by the equalities of left and right sides of Equations (3) and (3a).
Formulation of Non-Redox Systems
Example 1: The (static) system is formed from the following components: Na2S·9H2O (N01), Na2SO4·10H2O (N02) (Sal Mirabilis), H2O (N03). The species in the system thus formed, namely:
H2O (N1), H+1 (N2, n2), OH-1 (N3, n3), Na+1 (N4, n4), HSO4-1 (N5, n5), SO4-2 (N6, n6), H2S (N7, n7), HS-1 (N8, n8), S-2 (N9, n9) are involved in the following balances:
f0 = ChB:
N2 – N3 + N4 – N5 – 2N6 – N8 – 2N9 = 0
f1 = f(H):
2N1 + N2(1+2n2) + N3(1+2n3) + 2N4n4 + N5(1+2n5) + 2N6n6 + N7(2+2n7) + N8(1+2n8) + 2N9n9
= 18N01 + 20N02 + 2N03
f2 = f(O):
N1 + N2n2 + N3(1+n3) + N4n4 + N5(4+n5) + N6(4+n6) + N7n7 + N8n8 + N9n9 = 9N01 + 14N02 + N03
f12 = 2·f2 – f1:
= N2 + N3 + 7N5 + 8N6 – 2N7 – N8 = 8N02
– f3 = – f(Na):
2N01 + 2N02 = N4
– 6·f4 = 6·f(SO4):
6N02 = 6N5 + 6N6
2·f5 = 2·f(S):
2N7 + 2N8 + 2N9 = 2N01
f12 + f0 – f3 – 6·f4 + 2·f5
0 = 0
i.e., the linear combination (4) is transformed into identity; it can be rewritten into the form
(+1)·f1 + (–2)·f2 + (+1)·f3 + (+6)·f4 + (–2)·f5 – f0 = 0
(+1)·f(H) + (–2)·f(O) + (+1)·f(Na) + (+6)·f(SO4) + (–2)·f(S) – ChB = 0
where the numbers in round brackets as multipliers for fi (i=1,…,5) are equal to ONs of the related elements. Within f12, and then within (5), N1 and all niW values, within components and species, are cancelled. The species Xizi not involving H and/or O within XiZi , are also cancelled within f12. More specifically, the f3 involving only one kind of species, is considered here as equality, not as equation.
In this system, symproportionation [21] of sulfur does not occur; from this viewpoint, the system is at a metastable state [1,13]. Consequently, all elements (H, O, Na, S) involved in this system are perceived as fans, i.e., K* = K = 4. Sulfide oxidation can occur in presence of sulfate-reducing bacteria [34]. Sulfide gives sulfate after oxidation with H2O2 [35], whereas sulfate ions are not reducible in usual procedure [36].
The elemental balance for S is f*(S) = f45 = f4 + f5.
The linear combination f12 + f0 – f3 + p·f45
is not transformable into identity 0 = 0, at any p-value. From (6) and (4) we get the contradiction p =6 and p =–2, i.e., f45 is not applicable for checking f12 (Eq. 1) as the criterion of independency of the related balances.
Example 2 (dynamic system). V0 mL of titrand (D), containing ZnSO4 (C0) + NH3 (C1) + NH4Cl (C2) + NaH2In (erio T, C0In) is titrated with V mL of titrant (T) containing EDTA (C) [3].
The D is composed of N01 molecules of ZnSO4·7H2O (goslarite), N02 molecules of NH3, N03 molecules of NH4Cl, N04 molecules of NaH2In = C20H12N3O7SNa, N05 molecules of H2O and the T is composed of N06 molecules of EDTA = Na2H2L·2H2O = C10H14N2O8Na2·2H2O and N07 molecules of H2O, at defined point of titration (V mL of T added). In the D+T system, the following species are formed:
H2O (N1), H+1 (N2, n2), OH-1 (N3, n3), HSO4-1 (N4, n4), SO4-2 (N5, n5), Cl-1 (N6, n6), Na+1 (N7, n7), NH4 +1 (n8, N8), NH3 (n9,N9), Zn+2 (N10, n10), ZnOH+1 (N11, n11), soluble complex Zn(OH)2 (N12, n12), Zn(OH)3-1 (N13, n13), Zn(OH)4-2 (N14, n14),ZnNH3 +2 (N15, n15), Zn(NH3)2+2 (N16, n16), Zn(NH3)3+2 (N17,n17), Zn(NH3)4 +2 (N18, n18), ZnCl+1 (N19, n19); ZnSO4 (N20, n20), C20H13N3O7S (N21, n21), C20H12N3O7S-1 (N22, n22), C20H11N3O7S-2 (N23, n23), C20H10N3O7S-3 (N24, n24), C20H10N3O7SZn-1 (N25, n25), (C20H10N3O7S)2Zn-4 (N26, n26), C10H10N2O8+2 (H6L+2)
(N27, n27), C10H17N2O8+1 (H5L+1) (N28, n28), C10H16N2O8 (H4L) (N29, n29), C10H15N2O8-1 (H3L-1) (N30, n30), C10H14N2O8-2 (H2L-2) (N31, n31), C10H13N2O8-3 (HL-3) (N32, n32), C10H12N2O8-4 (L-4) (N33, n33), C10H13N2O8Zn-1 (ZnHL-1) (N34, n34), C10H12N2O8Zn-2 (ZnL-2) (N35, n35), C10H13N2O9Zn-3 (ZnOHL-3) (N36, n36).
In particular, the complex ZnOHL-3 is formed from ZnOH+1 and L-4.
The charge (ChB), elemental (f(H), f(O), f(Zn), f(Cl), f(Na)) and core (f(SO4), f(NH3), f(C20H10N3O7S), f(C10H12N2O8)) balances are written here as follows:
f0 = ChB:
N2 – N3 – N4 – 2N5 – N6 + N7 + N8 + 2N10 + N11 – N13 – 2N14 + 2N15 + 2N16 + 2N17 + 2N18 + N19 – N22 – 2N23
f1 = f(H) :
2N1 + N2(1 + 2n2) + N3(1 + 2n3) + N4(1 + 2n4) + 2N5n5 + 2N6n6 + 2N7n7 + N8(4 + 2n8) + N9(3 + 2n9) + 2N10n10
+ N11(1 + 2n11) + N12(2 + 2n12) + N13(3 + 2n13) + N14(4 + 2n14) + N15(3 + 2n15) + N16(6 + 2n16) + N17(9 + 2n17)
+ N18(12 + 2n18) + 2N19n19 + 2N20n20 + N21(13 + 2n21) + N22(12 + 2n22) + N23(11 + 2n23) + N24(10 + 2n24)
+ N25(10 + 2n25) + N26(20 + 2n26) + N27(18 + 2n27) + N28(17 + 2n28) + N29(16 + 2n29) + N30(15 + 2n30)
+ N31(14 + 2n31) + N32(13 + 2n32) + N33(12 + 2n33) + N34(13 + 2n34) + N35(12 + 2n35) + N36(13 + 2n36)
= 14N01 + 3N02 + 4N03 + 12N04 + 2N05 + 18N06 + 2N07
f2 = f(O) :
N1 + N2n2 + N3(1 + n3) + N4(4 + n4) + N5(4 + n5) + N6n6 + N7n7 + N8n8 + N9n9 + N10n10
+ N11(1 + n11) + N12(2 + n12) + N13(3 + n13) + N14(4 + n14) + N15n15 + N16n16 + N17n17
+ N18n18 + N19n19 + N20(4 + n20) + N21(7 + n21) + N22(7 + n22) + N23(7 + n23) + N24(7 + n24)
+ N25(7 + n25) + N26(14 + n26) + N27(8 + n27) + N28(8 + n28) + N29(8 + n29) + N30(8 + n30)
+ N31(8 + n31) + N32(8 + n32) + N33(8 + n33) + N34(8 + n34) + N35(8 + n35) + N36(9 + n36)= 11N01 + 7N04 + N05 + 10N06 + N07
– 2·f3 = – 2·f(Zn)
2N01 = 2N10 + 2N11 + 2N12 + 2N13 + 2N14 + 2N15 + 2N16 + 2N17 + 2N18 + 2N19 + 2N20 + 2N25 + 2N26 + 2N34 + 2N35 + 2N36
f4 = f(Cl):
N6 + N19 = N03
– f5 = – f(Na):
N04 + 2N06 = N7
– 6·f6 = – 6·f(SO4):
6N01 = 6N4 + 6N5 + 6N20
3·f7 = 3·f(NH3):
3N8 + 3N9 + 3N15 + 6N16 + 9N17 + 12N18 = 3N02 + 3N03
– f8 = – f(C20H10N3O7S):
N04 = N21 + N22 + N23 + N24 + N25 + 2N26
0·f9 = 0·f(C10H12N2O8):
0∙N27 + 0∙N28 + 0∙N29 + 0∙N30 + 0∙N31 + 0∙N32 + 0∙N33 + 0∙N34 + 0∙N35 + 0∙N36 = 0∙N06
The balance
f12 = 2·f(O) – f(H):
– N2 + N3 + 7N4 + 8N5 – 4N8 – 3N9 + N11 + 2N12 + 3N13 + 4N14 – 3N15 – 6N16 – 9N17 – 12N18 + 8N20 + N21 + 2N22 + 3N23 + 4N24 + 4N25 + 8N26 – 2N27 – N28 + N30 + 2N31 + 3N32 + 4N33 + 3N34 + 4N35 + 5N36
= 8N01 – 3N02 – 4N03 + 2N04 + 2N06
f0 + f12 – 2·f3 + f4 – f5 – 6·f6 + 3·f7 – f8 + 0·f9
0 = 0
i.e., the the linear combination (10) is transformed into identity, 0 = 0. It can be rewritten into the form
(+1)·f1 + (–2)·f2 + (+2)·f3 + (–1)·f4 + (+1)·f5 + (+6)·f6 + (–3)·f7 + (+1)·f8 + (0)·f9 – f0 = 0
i.e. the numbers in round brackets as multipliers for fi (i=1,…,9) are equal to ONs of the elements or charges ascribed to S in SO4-2, N in NH3, C20N3S in all the species of erio T, C10N2 in all the species of EDTA.
This system needs some further comments. All elements (H, O, Na, Cl, Zn, S, N, C) in involved in the components and species of the system are considered as fans, i.e., K* = K = 8. The number, 8, of the elements is lower than the total number of charge and elemental/core balances (K=1+9=10).
The formula C20H13N3O7S for the neutral species of erio T can be rewritten into the form (C20N3S)(H13O7) (C20N3S)1(H2O)6OH. The group of elements within C20N3S has the net charge x calculated from the equation 1∙x +6∙(0) + 1∙(-2+1) = 0 ⇒ x=+1. Similarly, in C10H16N2O8 = (C10N2) (H16O8) = (C10N2)1(H2O)8, the net charge x of the C10N2 group is calculated from the equation 1∙x + 8∙0 = 0, i.e., x = 0. The C20N3S+1 and C10N2 can be also (optionally) considered as cores.
The f6, f7, f8, f9 are specified separately, for different cores: SO4-2, NH3, C20H10N3O7S-3, C10H12N2O8 -4, resp. Note that S enters the compounds and species in f6, f8; N enters the compounds and species in f7, f8, f9; C enters the compounds and species in f8, f9. Furthermore, none transformations occur between the cores of the species belonging to separate concentration balances.
Referring again to the species involved with erio T, one can write the elemental balances: N21 + N22 + N23 + N24 + N25 + 2N26 = N04 (for S); 3N21 + 3N22 + 3N23 + 3N24 + 3N25 + 6N26 = 3N04 (for N); 20N21 + 20N22 + 20N23 + 20N24 + 20N25 + 40N26 = 20N04 (for C).
All the equations are identical and equivalent to Eq. (8), because the core C20H10N3O7S is unchanged in reactions occurred during the titration. Similarly, the species involved with EDTA fulfill the relations: 10N27 + 10N28 + 10N29 + 10N30 + 10N31 + 10N32 + 10N33 + 10N34 + 10N35 + 10N36 = 10N06 (for C), and 3N27 + 3N28 + 3N29 + 3N30 + 3N31 + 3N32 + 3N33 + 3N34 + 3N35 + 3N36 = 3N06 (for N). Both equations are equivalent to f9, Eq. (9).
Denoting the elemental balances for S, N and C as f*(S) = f68, f(N) = f789, f(C) = f89, we have the relations, expressed in the matrix form as follows
One can prove that the linear combination
f0 + f12 – 2·f3 + f4 – f5 + p∙f68 + q∙f789 + r∙f89
is not transformable into identity 0 = 0, at any of the (p, q, r) values. Namely, from Equations (10) and (12) we get
p (f6 + f8) + q(f7 + 3f8 + 2f9) + r(20f8 + 10f9) = p∙f6 + q∙f7 + (p+3q+20r)∙f8 + (2q+10r)∙f9
– 6∙f6 + 3∙f7 – f8 + 0∙f9 p = –6, q = 3, and p+3q+20r = –1, 2q+10r = 0
r = (–1 – (–6) – 3∙3)/20 = –0.2; r = –2∙3/10 = –0.6.
The r = -0.2 and r = -0.6 are contradictory values. Then the option given by Eq. 12, with f68, f789, f89, is not applicable for checking f12 (Eq. 1) as the criterion of independency of the related balances.
Formulation of Redox Systems
Example 3: We consider here
(1o) T subsystem (volume V mL), composed of KMnO4 (N01) + H2O (N02) + CO2 (N03);
(2o) D subsystem (V0 mL), composed of FeSO4∙7H2O (N04) + H2SO4 (N05) + H2O (N06) + CO2 (N07);
and
(3o) D+T redox system (V0+V mL), as the mixture of D and T, where the following species are formed:
H2O (N1); H+1 (N2, n2), OH-1 (N3, n3), HSO4-1 (N4, n4),SO4-2 (N5, n5), H2CO3 (N6, n6), HCO3-1 (N7, n7),CO3-2 (N8, n8), Fe+2 (N9, n9), FeOH+1 (N10, n10), FeSO4 (N11, n11),Fe+3 (N12, n12), FeOH+2 (N13, n13), Fe(OH)2+1 (N14, n14), Fe2(OH)2+4 (N15, n15); FeSO4+1 (N16, n16), Fe(SO4)2-1 (N17, n17), K+1 (N18, n18), MnO4-1 (N19, n19), MnO4-2 (N20, n20), Mn+3 (N21, n21), MnOH+2 (N22, n22), Mn+2 (N23, n23), MnOH+1 (N24, n24), MnSO4 (N25, n25)
The presence of CO2 in T and D is considered here as an admixture from air, to imitate real conditions of the analysis, on the step of preparation of D and T; the titration T(V) ⟹ D(V0) is realized in the closed system, under isothermal conditions. Precipitation of MnO2 does not occur at sufficiently low pH value [1].
The D+T dynamic redox system is then composed of nonredox static subsystems: D and T. On this basis, some general properties involved with non-redox and redox systems will be indicated. Different forms of GEB, resulting from linear combinations of charge and elemental balances related to D+T system, will be obtained.
To avoid (possible) disturbances, the common notation (subscripts) assumed in the set (14) of species will be applied for components and species in T, D and D+T. In context with the dynamic D+T system, T and D are considered as static (sub)systems.
Linear combination of balances
The T subsystem: We get here the balances:
f0 = ChB:
N2 – N3 – N7 – 2N8 + N18 – N19 = 0
f1 = f(H):
2N1 + N2(1+2n2) + N3(1+2n3) + N6(2+2n6) + N7(1+2n7) + 2N8n8 + 2N18n18 + 2N19n19 = 2N02
f2 = f(O):
N1 + N2n2 + N3(1+n3) + N6(3+n6) + N7(3+n7) + N8(3+n8) + N18n18 + N19(4+n19)
= 4N01 + N02 + 2N03
-4·f3 = -4·f(CO3) :
4N03 = 4N6 + 4N7 + 4N8
-f4 = -f(K) :
N01 = N18
-7·f5 = -7·f(Mn) :
7N01 = 7N19
f<12 = 2f2 – f1 = 2f(O) – f(H)
–N2 + N3+ 4N6 + 5N7 + 6N8 + 8N19 = 8N01 + 4N03
f12 + f0 – 4f3 – f4 – 7f5 = 0 ⟺ (+1)∙f1 + (–2)∙f2 + (+4)∙f3 + (+1)∙f4 + (+7)∙f5 – f0 = 0
(+1)∙f(H) + (–2)∙f(O) + (+4)∙f(CO3) + (+1)∙f(K) + (+7)∙f(Mn) – ChB = 0
0 = 0
i.e., the the linear combination (15) is transformed into identity, 0 = 0. The coefficients/multipliers at the balances f(Yk) are equal to ONs of elements in the corresponding species.
The D subsystem: We get here the balances:
f0 = ChB
N2 – N3 – N4 – 2N5 – N7 – 2N8 + 2N9 + N10 = 0
f1 = f(H)
2N1 + N2(1+2n2) + N3(1+2n3) + N4(1+2n4) + 2N5n5 + N6(2+2n6) + N7(1+2n7) + 2N8n8 + 2N9n9 + N10(1+2n10) + 2N11n11 = 14N04 + 2N05 + 2N06
f2 = f(O)
N1 + N2n2 + N3(1+n3) + N4(4+n4) + N5(4+n5) + N6(3+n6) + N7(3+n7) + N8(3+n8) + N9n9 +
N10(1+n10) + N11(4+n11) = 11N04 + 4N05 + N06 + 2N07
–4·f3 = –4·f(CO3)
4N07 = 4N6 + 4N7 + 4N8
–6·f6 = –6·f(SO4)
6N04 + 6N05 = 6N4 + 6N5 + 6N11
–2·f7 = –2·f(Fe)
2N04 = 2N9 + 2N10 + 2N11
f12 + f0 – 4·f3 – 6·f6 – 2·f7
0 = 0
i.e., the the linear combination (16) is transformed into identity, 0 = 0. From transformation of (16)
(+1)·f1 + (–2)·f2 + (+4)·f3 + (+6)·f6 + (+2)·f7 – f0
(+1)·f(H) + (–2)·f(O) + (+4)·f(CO3)+ (+6)·f(SO4) + (+2)·f(Fe) – ChB
we see again that the coefficients/multipliers at the balances f(Yk) are equal to ONs of elements in the corresponding species.
The D+T system
For the D+T system, from (14) we have the balances:
f0 = ChB
N2 – N3 – N4 – 2N5 – N7 – 2N8 + 2N9 + N10 + 3N12 + 2N13 + N14 + 4N15 + N16 – N17 + N18 – N19 – 2N20 +
3N21 + 2N22 + 2N23 + N24 = 0
f1 = f(H)
2N1 + N2(1+2n2) + N3(1+2n3) + N4(1+2n4) + 2N5n5 + N6(2+2n6) + N7(1+2n7) + 2N8n8 + 2N9n9 + N10(1+2n10) + 2N11n11 + 2N12n12 + N13(1+2n13) + N14(2+2n14) + N15(2+2n15) + 2N16n16 + 2N17n17 + 2N18n18 + 2N19n19 + 2N20n20 + 2N21n21 + N22(1+2n22) + 2N23n23 + N24(1+2n24) + 2N25n25
= 2N02 + 14N04 + 2N05 + 2N06
f2 = f(O)
N1 + N2n2 + N3(1+n3) + N4(4+n4) + N5(4+n5) + N6(3+n6) + N7(3+n7) + N8(3+n8) + N9n9 +
N10(1+n10) + N11(4+n11) + N12n12 + N13(1+n13) + N14(2+n14) + N15(2+n15) + N16(4+n16) + N17(8+n17) + N18n18 + N19(4+n19) + N20(4+n20) + N21n21 + N22(1+n22) + N23n23 + N24(1+n24) + N25(4+n25)
= 4N01 + N02 + 2N03 + 11N04 + 4N05 + N06 + 2N07
– 4·f3 = – 4·f(CO3):
4N03 + 4N07 = 4N6 + 4N7 + 4N8
– f4 = – f(K) :
N01 = N18
– f5 = – f(Mn)
N01 = N19 + N20 + N21 + N22 + N23 + N24 + N25
– 6·f6 = – 6·f(SO4)
6N04 + 6N05 = 6N4 + 6N5 + 6N11 + 6N16 + 12N17 + 6N25
– f7 = – f(Fe)
N04 = N9 + N10 + N11 + N12 + N13 + N14 + 2N15+ N16 + N17
Then we have, by turns,
f12 = 2·f(O) – f(H) :
– N2 + N3 + 7N4 + 8N5 + 4N6 + 5N7 + 6N8 + N10 + 8N11 + N13 + 2N14 + 2N15 + 8N16 + 16N17 + 8N19 + 8N20 + N22 + N24 + 8N25 = 8N01 + 4N03 + 8N04 + 6N05 + 4N07
f12 + f0 – 4·f3 – f4 – 6·f6:
2(N9+N10+N11) + 3(N12+N13+N14+2N15+N16+N17) + 7N19 + 6N20 + 3(N21+N22) + 2(N23+N24+N25) = 7N01 + 2N04
From transformation of (26) we have
(+1)ff1 + (-2)ff2 + (+4)ff3 + (+1)ff4 + (+6)ff6 – f0
(+1)·f(H) + (-2)·f(O) + (+4)·f(CO3) + (+1)·f(K) + (+6)·f(SO4)-ChB
We see that the coefficients/multipliers at the related balances fk (k=1,2,3,4,6) are equal to ONs of elements in the corresponding species; the balances fk in (28) are related to fans.
Applying the relations:
[ XiZi ]·(V0+V) = 103·Ni/NA , CV = 103·N01/NA ,
C0V0 = 103·N04/NA , C1V = 103·N03/NA ,
C01V0 = 103·N05/NA , C02V0 = 103·N07/NA.
we rewrite Eq. (26) in the more explicit form as
2([Fe+2] + [FeOH+1] + [FeSO4]) + 3([Fe+3] + [FeOH+2] + [Fe(OH)2+1] + 2[Fe2(OH)2+4] + [FeSO4+1] + [Fe(SO4)2 -1])
+ 7[MnO4-1] + 6[MnO4-2] + 3([Mn+3] + [MnOH+2]) + 2([Mn+2]+ [MnOH+1] + [MnSO4])
= (7CV + 2C0V0)/(V0+V)
Eq. (30), obtained from (25,28,29), consists only of the species, where players are involved. Other linear combinations were also used. Applying atomic numbers: ZMn = 25 and ZFe = 26, we have
ZFe·f7 + ZMn·f5 - (f12 + f0 - 4·f3 - f4 - 6·f6) :
(ZFe–2)·(N9+N10+N11) + (ZFe– 3)·(N12+N13+N14+2N15+N16+N17) + (ZMn–7)·N19 + (ZMn–6)·N20 + (ZMn–3)·(N21+N22) + (ZMn–2)·(N23+N24+N25) = (ZFe–2)·N04 + (ZMn–7)·N01
(ZFe–2)·([Fe+2] + [FeOH+1] + [FeSO4]) + (ZFe–3)·([Fe+3] + [FeOH+2] + [Fe(OH)2+1]+2[Fe2(OH)2+4] + [FeSO4+1] + [Fe(SO4)2 -1])+(ZMn–7)·[MnO4–1] + (ZMn–6)·[MnO4–2] + (ZMn–3)·([Mn+3] + [MnOH+2]) + (ZMn–2)·([Mn+2]+[MnOH+1] + [MnSO4])
= ((ZFe–2)·C0V0 + (ZMn–7)·CV)/(V0+V)
Equation (32) results innediately from the Approach I to GEB, see [6].
The least extended (the most compact) form is as follows [8,25]
3·f7 + 2·f5 – (f12 + f0 – 4·f3 – f4 – 6·f6):
(N9 + N10 + N11) – (5N19 + 4N20 + N21 + N22) = N04 – 5N01 · [Fe+2] + [FeOH+1] + [FeSO4] – (5[MnO4–1] + 4[MnO4–2] +[Mn+3] + [MnOH+2])
-(C0V0 – 5·CV)/(V0+V)=0
Eq. (25) for f12 (24), considered as pr-GEB (Eq. 1), can also be rewritten in terms of concentrations; we have
– [H+1] + [OH-1] + 7[HSO4-1] + 8[SO4-2] + 4[H2CO3] +5[HCO3 -1] + 6[CO3-2] + [FeOH+1] + 8[FeSO4] +[FeOH+2] +2[Fe(OH)2 +1] + 8[Fe(SO4+1] + 16[Fe(SO4)2-1] + 8[MnO4-1] + 8[MnO4-2] + [MnOH+2] + [MnOH+1] + 8[MnSO4]
= (8CV + 8C0V0 + 4C1V + 6C01V0 + 4C02V0)/(V0+V)
Equations 30, 32–34 are equivalent forms of GEB for this system. Other linear combinations of the balances are also admitted/possible for this purpose; none of them are reduced to the identity 0 = 0. However, the shortest Eq. (33), chosen arbitrarily, seems to be the most useful for calculation purposes–for obvious reasons.
The T and D are non redox subsystems of the redox D+T system; this is not the general regularity, of course. In some other systems, D or T or both (D and T) can form redox subsystems. For example, the Br2 solution considered in [5,6,37,38] is the redox subsystem D; I2 + KI solution is the redox subystem T in [39].
Calculation Procedure for the D+T System
Completing the set of independent balances
Equation 33 is completed by charge and concentration balances, obtained from Equations 18, 19, 21, 22, 23 and relations (29). We have, by turns,
[H+1] – [OH-1] – [HSO4-1] – 2[SO4-2] – [HCO3-1] – 2[CO3-2] + 2[Fe+2] + [FeOH+1] + 3[Fe+3] + 2[FeOH+2] + [Fe(OH)2+1]+ 4[Fe2(OH)2+4] + [FeSO4+1] – [Fe(SO4)2-1] + [K+1] – [MnO4 -1] –2[MnO4-2] + 3[Mn+3] + 2[MnOH+2] + 2[Mn+2] + [MnOH+1] = 0
[H2CO3] + [HCO3-1] + [CO3-2] – (C02V0+C1V)/(V0+V) = 0
[MnO4-1] + [MnO4-2] + [Mn+3] + [MnOH+2] + [Mn+2] + [MnOH+1] + [MnSO4] – CV/(V0+V) = 0
[HSO4-1] + [SO4-2] + [FeSO4] + [FeSO4+1] + 2[Fe(SO4)2-1] + [MnSO4] – (C0+C01)V0/(V0+V) = 0
[Fe+2] + [FeOH+1] + [FeSO4] + [Fe+3] + [FeOH+2] +[Fe(OH)2+1] + 2[Fe2(OH)2+4]+[FeSO4+1] + [Fe(SO4)2-1] – C0V0/(V0+V) = 0
The equality (not equation!)
[K+1] = CV/(V0+V)
can enter immediately Eq. 18a like a number, at defined V-value.
The set of interrelations for equilibrium constants
Concentrations of the species involved in the set of 6 equations: 33, 18a, 19a, 21a, 22a, 23a, are compatible with the complete set of equilibrium constants, specified as follows:
[H+1] [OH-1] = 10-14.0; [HSO4-1] = 101.8[H+1][SO4-2];
[H2CO3] = 1016.4[H+1]2[CO32];[HCO3-1] = 1010.1[H+1] [CO3-2];
[Fe+3] = [Fe+2]∙10A(E – 0.771); [FeOH+1] =104.5[Fe+2][OH-1];
[FeOH+2] = 1011.0[Fe+3][OH-1]; [Fe(OH)2+1] =
1021.7[Fe+3][OH-1]2; [Fe2(OH)2+4] = 1021.7[Fe+3]2[OH-1]2;
[FeSO4] = 102.3[Fe+2][SO4-2]; [FeSO4+1] = 104.18[Fe+3][SO4-2];
[Fe(SO4)2-1] = 107.4[Fe+3][SO4-2]2;
[MnO4-1] = [Mn+2]∙105A(E – 1.507) + 8pH;
[MnO4-2] = [Mn+2]∙104A(E – 1.743) + 8pH;
[Mn+3] = [Mn+2]∙10A(E – 1.509);
[MnOH+2] = 1014.2[Mn+3][OH-1]
The electrode potentials E [V] are put in context with standard electrode potentials E0i, expressed in SHE scale [40].
6 independent variables, chosen as components of the vector:
x = [x1,…,x6]T = [E,pH,pMn2,pFe2,pSO4,pH2CO3]T
where E – potential [V], pH = – log[H+1], pMn2 = – log[Mn+2], pFe2 = – log[Fe+2], pSO4 = – log[SO4 -2], pH2CO3 = – log[H2CO3].
Mole fraction as the parameter of D+T system
All the variables, put in logarithmic scale, are considered as functions of volume V of the titrant T added during the titration T ⇨ D, xi = x i(V). The V [mL] is considered as parameter of the D+T system. On this basis, the mole fraction values
are calculated at pre-assumed V0, C, C0 values. The Φ provides a kind of normalization (independence on V0 value) in the system, and is taken as the independent variable on the abscissa of the related plots. The knowledge of the xi = xi (V) values, allows also to calculate the concentrations of the different species of the D+T system on the basis of relations (35) and present these changes as plots on the relevant speciation diagrams log , together with E = E(Φ) and pH = pH (Φ) relationships. Graphical presentation of the data provides an excellent tool for qualitative and quantitative evaluation of processes, occurring at any point of the titration.
All these data for the D+T system are obtained on the basis of calculations realized with use of the MATLAB [1] computer program.
Computer program
function F = Function_MnO4_Fe(x)
global V Vmin Vstep Vmax V0 C C1 C0 C01 C02 H OH fi pH E
global Kw pKw A K logK
global HSO4 SO4 logHSO4 logSO4
global H2CO3 HCO3 CO3
global logH2CO3 logHCO3 logCO3
global Mn7O4 Mn6O4 Mn3 Mn3OH
global logMn7O4 logMn6O4 logMn3 logMn3OH
global Mn2 Mn2OH Mn2SO4
global logMn2 logMn2OH logMn2SO4
global Fe2 Fe2OH Fe2SO4
global logFe2 logFe2OH logFe2SO4
global Fe3 Fe3OH Fe3OH2 Fe32OH2 Fe3SO4 Fe3SO42
global logFe3 logFe3OH logFe3OH2 logFe32OH2 logFe3SO4 logFe3SO42
E=x(1);
pH=x(2);
Mn2=10.^-x(3);
Fe2=10.^-x(4);
SO4=10.^-x(5);
H2CO3=10.^-x(6);
H=10.^-pH;
pKw=14;
Kw=10.^-14;
OH=Kw./H;
A=16.9;
Mn7O4=Mn2.*10.^(5.*A.*(E-1.507)+8.*pH);
Mn6O4=Mn2.*10.^(4.*A.*(E-1.743)+8.*pH);
Mn3=Mn2.*10.^(A.*(E-1.509));
Fe3=Fe2.*10.^(A.*(E-0.771));
HSO4=10.^1.8.*H.*SO4;
CO3=10.^-16.4*H^-2*H2CO3;
HCO3=10.^10.1*H*CO3;
Fe2OH=10.^4.5.*Fe2.*OH;
Fe2SO4=10.^2.3.*Fe2.*SO4;
Fe3OH=10.^11.0.*Fe3.*OH;
Fe3OH2=10.^21.7.*Fe3.*OH.^2;
Fe32OH2=10.^25.1.*Fe3.^2.*OH.^2;
Fe3SO4=10.^4.18.*Fe3.*SO4;
Fe3SO42=10.^7.4.*Fe3.*SO4.^2;
Mn2OH=10.^3.4.*Mn2.*OH;
Mn2SO4=10.^2.28.*Mn2.*SO4;
Mn3OH=10.^14.2.*Mn3.*OH;
K=C.*V./(V0+V);
%Charge balance
F=[(H-OH -HSO4-2.*SO4-HCO3-2.*CO3-+2.*Fe2+Fe2OH... +3.*Fe3+2.*Fe3OH+Fe3OH2+4.*Fe32OH2+Fe3SO4- Fe3SO42...
+K-Mn7O4-2.*Mn6O4+3*Mn3+2.*Mn3OH+2.*Mn2+Mn2 OH);
Figure 1:
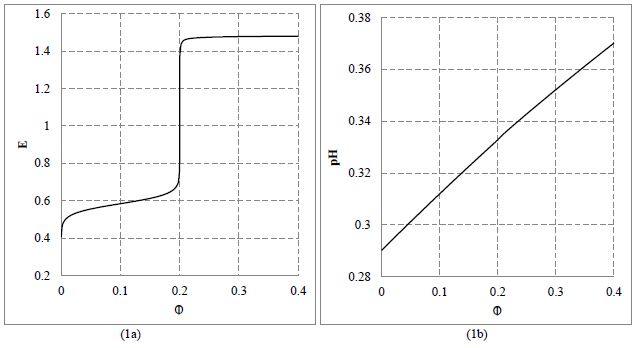
The relationships: (1a) E = E ( Φ ) and (1b) pH = pH ( Φ ) plotted at (V0, C0, C01, C) = (100, 0.01, 0.5, 0.02) and C1 = C02 = 0.
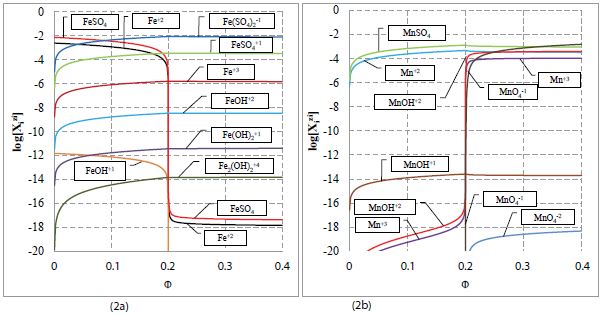
Figure 2: The speciation curves for (2a) Mn species and (2b) Fe species plotted at (V0, C0, C01, C) = (100, 0.01, 0.5, 0.02) and C1 = C02 = 0.
%Concentration balance of Mn
(Mn7O4+Mn6O4+Mn3+Mn3OH+Mn2+Mn2OH+Mn2 SO4-C.*V./(V0+V));
%Concentration balance of Fe
(Fe2+Fe2OH+Fe2SO4+Fe3+Fe3OH+Fe3OH2+2.*Fe32 OH2...+Fe3SO4+Fe3SO42-C0.*V0./(V0+V));
%Concentration balance of SO4
(HSO4+SO4+Mn2SO4+Fe2SO4+Fe3SO4+2.*Fe3SO42- (C0+Ca).*V0./(V0+V));
%Concentration balance of CO3
(H2CO3+HCO3+CO3-(C02.*V0+C1.*V)/(V0+V));
%Electron balance
(Fe2+Fe2OH+Fe2SO4-(5.*Mn7O4+4.*Mn6O4+ Mn3+Mn3OH)... -(C0.*V0.-5.*C.*V.)/(V0+V))];
logMn2=log10(Mn2);
logMn2OH=log10(Mn2OH);
Table 3:The selected pairs ( Φ , E) taken from the vicinity of Φeq = 0.2 at (V0, C0, C01, C) = (100, 0.01, 0.5, 0.02) and C1 = C02 = 0.
| Φ | E, mV |
|---|---|
| 0.19800 | 0.701 |
| 0.19900 | 0.719 |
| 0.19980 | 0.761 |
| 0.19990 | 0.778 |
| 0.19998 | 0.820 |
| 0.20000 | 1.034 |
| 0.20002 | 1.323 |
| 0.20010 | 1.365 |
| 0.20020 | 1.382 |
| 0.20200 | 1.442 |
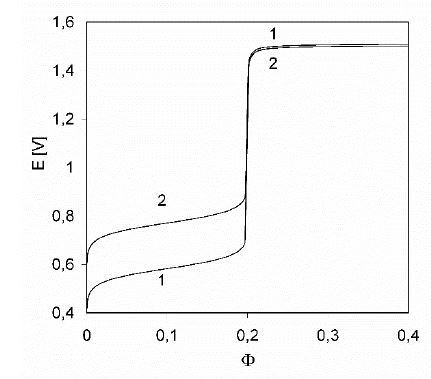
Figure 3: The E = E( Φ ) relationships: 1 –as in Figure 1a; 2 –after omission of sulphate Fe- and Mn- complexes in the related balances; C0 = 0.01, C01 = 0.5, C = 0.02.
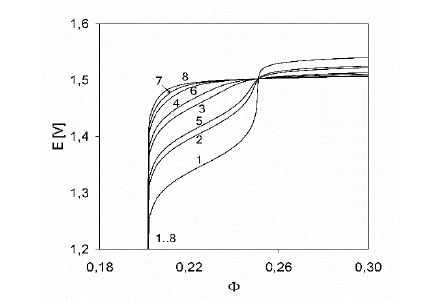
Figure 4: Fragments of hypothetical titration curves plotted for different pairs of stability constants (K1, K2) of the sulfate complexes Mn (SO4)i +3–2i: 1 – (104, 107), 2 – (103, 106), 3 – (102.5, 105), 4 – (102, 104), 5 – (104, 0), 6 – (103, 0), 7 – (102, 0), 8 – (0, 0), plotted at C0 = 0.01, C01 = 0.5, C = 0.02.
logMn2SO4=log10(Mn2SO4); logMn3=log10(Mn3); logMn3OH=log10(Mn3OH); logMn6O4=log10(Mn6O4); logMn7O4=log10(Mn7O4); logFe2=log10(Fe2); logFe2OH=log10(Fe2OH); logFe2SO4=log10(Fe2SO4); logFe3=log10(Fe3); logFe3OH=log10(Fe3OH); logFe3OH2=log10(Fe3OH2); logFe32OH2=log10(Fe32OH2); logFe3SO4=log10(Fe3SO4); logFe3SO42=log10(Fe3SO42); logHSO4=log10(HSO4); logSO4=log10(SO4); logH2CO3=log10(H2CO3); logHCO3=log10(HCO3); logCO3=log10(CO3); logK=log10(K);
Graphical presentation of results and discussion
The results of calculations made at V0=100, C0=0.01, C=0.02, C01=0.5, C02=C1 = 0 are plotted in Figures 1 and 2. The jump of E on the curve in Fig. 1a occurs at Φ = Φeq = 0.2, i.e., at the equivalent (eq) point where C∙Veq = 0.2·C0∙V0. Relatively small pH changes (Figure 1b) result from high buffer capacity of the titrand D [41-46]. From Figure 2a we see that [Fe+3] << [FeSO4 +1] << [Fe(SO4)2 -1]. Note that MnOH+2 and Mn+3 (not MnO4 -1) ions are the predominating manganese species immediately after crossing the related equivalence point (Figure 2b), Some points from the vicinity of equivalence point are presented in Table 1.
Variations on a theme
Option 1. To indicate a complexation effect of sulphate ions, introduced by the H2SO4 solution, we compare the plots of E = E(Φ) curves: (1) the curve from Fig. 1a with one (2) obtained after omission of the sulfate complexes (FeSO4, FeSO4+1, Fe(SO4)2-1, MnSO4) from the algorithm in section 4.5. The related plots are compared in Figure 3.
Option 2. The sulphate complexes formed by Mn+3 ions are unknown in literature, although on the basis of analogy with other trivalent ions (e.g., Fe+3, Al+3) it could be expected that the stability constants Ki for virtual Mn(SO4)i +3-2i complexes, [Mn(SO4)i+3-2i] = Ki·[Mn+3] [SO4 -2]i, may have significant values. However, a numerical analysis of the data obtained for the pre-assumed stability constants Ki of sulphate complexes (Figure 4) with the curve obtained experimentally [14] has revealed that the Mn(SO4)i +3-2i complexes – if they exist – are relatively weak [6].
Final Comments
The quantitative, algebraic description of any electrolytic system according to GATES principles is based on electro neutrality rule, and on rules of conservation of particular elements in the systems, where none radioactive transformations occur [2]. The electro-neutrality rule is expressed by charge balance (f0 = ChB). The conservation of particular elements is expressed in terms of elemental and core balances fk = f(Yk), where Yk (k=1,2,…,K) is an element or core. For ordering purposes, it is assumed that Y1 = H, Y2 = O, and the linear combination f12 = 2·f2 – f1 = 2∙f(O) – f(H) is formulated. In redox systems, K* electron-non-active elements/cores (‘fans’), and K–K* electron-active elements (‘players’) are distinguished. In all examples presented here, H and O did not participate in redox systems as players. The set of K balances (f0, f12, f3,…, fk) is needed for mathematical formulation of a redox system (i.e., at K* < K), whereas the K–1 balances f0, f3,…, fk are needed for resolution of a non-redox system, where K* = K and f12 is the balance linearly dependent on f0, f3,…,fk. The linear independency or dependency of f12 within the balances f0, f12, f3,…,fk is then the general, dichotomous criterion distinguishing between redox and non-redox systems. The linear combination * (Eq. 3) applied to a non-redox system (1º) gives the identity, 0 = 0, for a non-redox system, or (2 º) does not give the identity for a redox system, also after any linear combination with K - K* balances for the players in this system. These regularities are valid for coefficients dk equal to oxidation numbers (ONs) of the elements in the corresponding balances fk = f(Yk) for elements/cores Yk related to fans.
The f12 and any linear combination of f12 with f0, f3,…, fk, have full properties of Generalized Electron Balance (GEB), completing the set of K balances, f0,f12,f3,…,fk, needed for resolution of a redox system, of any degree of complexity. The supreme role of this independency/dependency criterion, put also in context with calculation of ONs, is of great importance, in context with the contractual nature of the ON concept known from the literature issued hitherto [47-49]. These regularities are the clear confirmation of the Emmy Noether’s general theorem [50] applied to conservation laws of a physical/electrolytic system, expressed in terms of algebraic equations, where GEB is perceived as the Law of Nature [15], as the hidden connection of physicochemical laws, and as the breakthrough in thermodynamic theory of electrolytic redox systems. Resolution of several redox systems, according to principles of Generalized Approach to Electrolytic Systems (GATES), is presented. The GATES/ GEB is the best thermodynamic approach of electrolytic redox systems, of any degree of complexity. The Generalized Equivalent Mass (GEM) concept [14], fully compatible with the GATES principles, was introduced. The mathematical models, applicable for handling the results obtained from potentiometric titrations in redox systems, were also presented. The chapter offers – undoubtedly – the best possible ways to resolution of the issues raised. Formulation of an electrolytic redox system specified in section 3.1.3 illustrates the huge possibilities/advantages inherent in GATES/GEB.
All the regularities specified above are valid for redox and non-redox systems of any degree of complexity, also for the multi-solvent systems [51-54].
The key role of H and O (not free electrons, e-1) in redox systems, inherent in f12, was stressed in [23]. Contrary to appearances, established by the current paradigm “obligatory” till now, the criterion distinguishing non-redox and redox systems is not immediately associated with free electrons in the system. The new/fundamental/practical criterion involved with f12 = 2∙f(O) - f(H) and its properties, unknown in earlier literature, provides a kind of uniformity in the formulas derived for this purpose. This fact, especially the simple calculations of free electron concentrations in redox systems [23], deny the unique role of free electrons in redox reactions. On the other hand, it points to the decisive role of H and O in redox systems [2], suggested elsewhere, in earlier theoretical/hypothetical considerations on these systems. Here is the hidden simplicity, which had to be discovered, as the Approach II to GEB. The author ™ contends that the discovery of the Approach II GEB would most likely be impossible without the prior discovery of the Approach I to GEB.
The GEB concept, valid for electrolytic redox systems, is the emanation of balances for H and O, referred to aqueous media. GEB is compatible with other (charge and concentration) balances and enables to resolve the electrolytic (mono- or/and two-phase) redox systems of any degree of complexity, within the scope of GATES, perceived as the thermodynamic approach to equilibrium and metastable systems, where all necessary physicochemical knowledge on the systems tested is involved. The GATES is perceived as the unrivalled tool applicable, among others: (a) to mathematical modelling of thermodynamic behavior of the systems, (b) in choice of optimal a priori conditions of chemical analyses, and (c) in gaining chemical information invisible in real experiments, in general.
GATES/GEB is a counter-proposal in relation to earlier IUPAC decisions, presented in three subsequent editions of the Orange Book, and based on the reaction stoichiometry; that viewpoint was criticized unequivocally/exhaustively/ convincingly, especially in a series of authors’ articles cited herein. It was demonstrated, on examples of redox systems of different complexity, that stoichiometry is a secondary/ derivative/ “fragile” concept, from the viewpoint of GATES, and GATES/ GEB, in particular.
Conservation laws of physics are very closely related to the symmetry of physical laws under various transformations. The nature of these connections is an intriguing physical problem. The theory of these connections, as it appears in classical physics, constitutes one of the most beautiful aspects of mathematical physics. It confirms a general theorem of Emmy Noether which states that symmetries and conservation laws of a physical system correspond to each other [50]. The Noether's conceptual approach to algebra led to a body of principles unifying algebra, geometry, linear algebra, topology, and logic. The theory of this connection constitutes one of the most beautiful chapters of mathematical physics.
Concluding, GATES is the overall, thermodynamic approach to redox and non-redox, static and dynamic, single and multiphase equilibrium, metastable and nonequilibrium electrolytic systems, of any degree of complexity. Possibilities of GATES/GEB are far greater than ones offered by the actual physicochemical knowledge related to the system in question.
Stoichiometry, oxidation number, equivalent mass, order of reaction, equivalent mass [14], etc. are derivative (not primary!) concepts within GATES. The Equilibrium Law (EL), based on the Gibbs function and the Lagrange multipliers idea [15], can be put instead of Mass Action Law (MAL), based on a stoichiometric reaction notation, and other principles. Equilibrium, kinetic and metastable systems are distinguished. Within GATES, thermodynamics of electrolytic systems is based on purely algebraic principles; the stoichiometry is considered here only as a kind of “dummy” [22,23,55].
Summarizing, this paper offers the best possible ways to resolution of the issues raised.
Michałowski T (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems, Chapter 1 (pp: 1-34) in: Applications of MATLAB in Science and Engineering (ed. by T. Michałowski), InTech - Open Access publisher in the fields of Science, Technology and Medicine.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2014) GATES as the Unique Tool for Simulation of Electrolytic Redox and Non-Redox Systems. Journal of Analytical and Bioanalytical Techniques 5: 204.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2014) Linear Dependence of Balances for Non-Redox Electrolytic Systems. American Journal of Analytical Chemistry 5: 1285-1289.[ Ref ]
Michalowski T (1994) Calculation of pH and potential E for bromine aqueous solutions. J. Chem. Educ 71: 560-562.[ Ref ]
Michałowski T, Lesiak A (1994) Acid-base titration curves in disproportionating redox systems. J. Chem. Educ 71: 632-636.[ Ref ]
Michałowski T, Lesiak A (1994) Formulation of generalized equations for redox titration curves. Chem. Anal. (Warsaw) 39: 623-637.[ Ref ]
Michałowski T, Wajda N, Janecki D (1996) A Unified Quantitative Approach to Electrolytic Systems. Chem. Anal. (Warsaw) 41: 667-685.[ Ref ]
Michałowski T, Baterowicz A, Madej A, Kochana J (2001) An extended Gran method and its applicability for simultaneous determination of Fe(II) and Fe(III), Analytica Chimica Acta 442: 287-293.[ Ref ]
Michałowski T, Rymanowski M, Pietrzyk A (2005) Non-typical Brönsted’s acids and bases. Journal of Chemical Education 82: 470-472.[ Ref ]
Michałowski T, Toporek M, Rymanowski M (2005) Overview on the Gran and other linearization methods applied in titrimetric analyses. Talanta 65: 1241-1253.[ Ref ]
Michałowski T, Kupiec K, Rymanowski M (2008) Numerical analysis of the Gran methods. A comparative study. Analytica Chimica Acta 606: 172-183.[ Ref ]
Ponikvar M, Michałowski T, Kupiec K, Wybraniec S, Rymanowski M (2008) Experimental verification of the modified Gran methods applicable to redox systems. Analytica Chimica Acta 628: 181-189.[ Ref ]
Michałowski T (2010) The Generalized Approach to Electrolytic Systems: I. Physicochemical and Analytical Implications. Critical Reviews in Analytical Chemistry 40: 2-16.[ Ref ]
Michałowski T, Pietrzyk A, Ponikvar-Svet M, Rymanowski M (2010) The Generalized Approach to Electrolytic Systems: II. The Generalized Equivalent Mass (GEM) Concept. Critical Reviews in Analytical Chemistry 40: 17-29.[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Generalized Electron Balance (GEB) as the Law of Nature in Electrolytic Redox Systems, in: Redox: Principles and Advanced Applications, Ali Khalid, M.A. (Ed.) InTech Chap. 2: 9-55.[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Formulation of simple electrolytic redox systems according to GATES/ GEB principles. Journal of Chemistry and Applied Chemical Engineering 1: 1-10.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2013) Comparative balancing of non-redox and redox electrolytic systems and its consequences. American Journal of Analytical Chemistry 4: 46-53.[ Ref ]
Michałowski T, Toporek M, Michałowska-Kaczmarczyk AM, Asuero AG (2013) New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta 109: 519-531.[ Ref ]
Michałowski T, Michałowska-Kaczmarczyk AM, Toporek M (2013) Formulation of general criterion distinguishing between non-redox and redox systems. Electrochimica Acta 112: 199-211.[ Ref ]
Michałowska-Kaczmarczyk AM, Toporek M, Michałowski T (2015) Speciation Diagrams in Dynamic Iodide + Dichromate System. Electrochimica Acta 155: 217-227.[ Ref ]
Toporek M, Michałowska-Kaczmarczyk AM, Michałowski T (2015) Symproportionation versus Disproportionation in Bromine Redox Systems. Electrochimica Acta 171: 176-187.[ Ref ]
Michałowska-Kaczmarczyk AM, Asuero AG, Toporek M, Michałowski T (2015) “Why not stoichiometry” versus “Stoichiometry-why not?” Part II. GATES in context with redox systems, Critical Reviews in Analytical Chemistry 45: 241-2689.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T, Toporek M, Asuero AG (2015) “Why not stoichiometry” versus “Stoichiometry – why not?” Part III, Extension of GATES/GEB on Complex Dynamic Redox Systems. Critical Reviews in Analytical Chemistry 45: 348-366.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T, Toporek M (2016) Formulation of Dynamic Redox Systems according to GATES/GEB Principles. International Journal of Electrochemical Science 11: 2560- 2578.[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) A Distinguishing Feature of the Balance 2∙f(O)–f(H) in Electrolytic Systems. The Reference to Titrimetric Methods of Analysis, in: Advances in Titration Techniques. Vu Dang Hoang (Ed.), InTech Chap 6: 173-207.[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) General Properties of the Balances 2∙f(O)-f(H) Related to Electrolytic Systems. Analytical Chemistry: An Indian Journal 17: 124-147.[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Oxidation number, oxidant and reductant as derivative concepts within GATES/GEB formulation. Journal of Chemistry and Applied Chemical Engineering 1: 2.[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Some Regularities Involved with Oxidation Numbers Stated in Formulation of Redox Systems According to GATES/GEB Principles. Journal of Analytical, Bioanalytical and Separation Techniques 2: 102- 110.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2018) The Importance of Linear Combinations in Theory of Electrolytic Systems. Austin Chemical Engineering 5: 1060.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2018) The modified Gran methods in potentiometric redox titrations derived according to GATES/GEB principles. Journal of Chemical Engineering and Bioanalytical Chemistry 2: 88-113.[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2018) The balance 2∙f(O)–f(H) as a keystone in formulation of electrolytic systems. Research and Reviews in Computational Chemistry 1: 1-9.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2018) The Balance 2∙f(O)–f(H) as a Cornerstone in Formulation of Electrolytic Systems. Journal of New Developments in Chemistry 2: 1-13.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2018) The distinguishing role of 2·f(O)–f(H) in electrolytic systems. Biomedical Journal of Scientific and Technical Research 8: 6237- 6246.[ Ref ]
Fuseler K, Krekeler D, Sydow U, Cypionka H (1996) A common pathway of sulfide oxidation by sulfate-reducing bacteria. FEMS Microbiology Letters 144: 129-134.[ Ref ]
Lange L, Triebel W (2000) "Sulfides, Polysulfides, and Sulfanes". Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim.[ Ref ]
Bo-Qing Xu, W.M.H. Sachtler (1997) Reduction of SO4= ions in Sulfated Zirconia Catalysts. Journal of Catalysis 167: 224-233.[ Ref ]
Meija J, Michałowska-Kaczmarczyk AM, Michałowski T (2017) Redox titration challenge. Analytical and Bioanalytical Chemistry 409: 11-13.[ Ref ]
Michałowski T, Michałowska-Kaczmarczyk AM, Meija J (2017) Solution of redox titration challenge. Analytical and Bioanalytical Chemistry 409: 4113-4115.[ Ref ]
Michałowski T, Ponikvar-Svet M, Asuero AG, Kupiec K (2012) Thermodynamic and kinetic effects involved with pH titration of As(III) with iodine in a buffered malonate system. Journal of Solution Chemistry 41: 436-446.[ Ref ]
Standard Electrode Potentials, http://hyperphysics.phy-astr.gsu.edu/ hbase/Chemical/electrode.html[ Ref ]
Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Dynamic Buffer Capacities in Redox Systems. Journal of Chemistry and Applied Chemical Engineering, 1: 1-7.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2015) Dynamic Buffer Capacity in Acid-Base Systems. Journal of Solution Chemistry 44: 1256- 1266.[ Ref ]
Asuero AG, Michałowski T (2011) Comprehensive formulation of titration curves referred to complex acid-base systems and its analytical implications. Critical Reviews in Analytical Chemistry 41: 151-187.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T, Asuero AG (2015) Formulation of dynamic buffer capacity for phytic acid. American Journal of Chemistry and Applications 2: 5-9.[ Ref ]
Michałowski T, Asuero AG (2012) New approaches in modelling the carbonate alkalinity and total alkalinity. Critical Reviews in Analytical Chemistry 42: 220-244.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2016) Application of Simms Constants in Modeling the Titrimetric Analyses of Fulvic Acids and Their Complexes with Metal Ions. Journal of Solution Chemistry 45: 200-220.[ Ref ]
Karen P, McArdle P, Takats J (2014) Toward a comprehensive definition of oxidation state (IUPAC Technical Report). Pure and Applied Chemistry 86: 1017-1081.[ Ref ]
Karen P (2015) Oxidation state, a long-standing issue! Angewandte Chemie International Edition in English 54: 4716-4726.[ Ref ]
Karen P, McArdle P, Takats J (2016) Comprehensive definition of oxidation state (IUPAC Recommendations 2016). Pure and Applied Chemistry 88: 831-839.[ Ref ]
Noether E (1918) Invariante Variationsproblem, Nachrichten der Königlichen Gesellschaft der Wissenschaften zu Göttingen Mathematisch-Physikalischen Klasse 237-257[ Ref ]
Michałowski T, Pilarski B, Dobkowska A, Młodzianowski J (2010) Mathematical modeling and physicochemical studies on acid-base equilibria in binary-solvent systems. Wiadomości Chemiczne 54: 124- 154.[ Ref ]
Pilarski B, Dobkowska A, Foks H, Michałowski T (2010) Modelling of acid–base equilibria in binary-solvent systems: A comparative study. Talanta 80: 1073-1080.[ Ref ]
Michałowski T, Pilarski B, Asuero AG, Michałowska-Kaczmarczyk AM (2014) Modeling of Acid-Base Properties in Binary-Solvent Systems. 9.4, pp. 623-648 in "Handbook of Solvents" (Vol 1) Properties, G. Wypych (Editor), ChemTec Publishing, Toronto.[ Ref ]
Michałowska-Kaczmarczyk AM, Michałowski T (2014) Generalized Electron Balance for Dynamic Redox Systems in Mixed-Solvent Media. Journal of Analytical Sciences, Methods and Instrumentation 4: 102-109.[ Ref ]
Michałowska-Kaczmarczyk AM, Asuero AG, Michałowski T (2015) “Why not stoichiometry” versus “Stoichiometry – why not?” Part I. General context. Critical Reviews in Analytical Chemistry 45: 166-188.[ Ref ]