Journal Name: Journal of Applied Microbiological Research
Article Type: Research
Received date: 13 August, 2020
Accepted date: 27 October, 2020
Published date: 2021-01-09
Citation: Adam IEM, Abdokashif I, Elrashid A, Bayoumi H, Musa A, et al. (2020) Novel Algorithms for PFGE Bacterial Typing: Number of Co-Migrated DNA Fragments, Linking PFGE to WGS Results and Computer simulations for Evaluation of PulseNet International Typing Protocols. J Appl Microb Res. Vol: 3 Issu: 2 (52-67).
Copyright: © 2020 Adam IEM et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background: Standard protocols for Pulsed-field gel electrophoresis (PFGE) were adopted and being used in a global scale for surveillance of many bacterial food-borne diseases. Matched PFGE bands are considered according to values of retention factors (rF) regardless of co-migration of different DNA fragments (having equal or very close molecular weight). Molecular epidemiology is turning toward whole genome sequencing (WGS), WGS results are compared using different DNA sequence alignment methods. Although, WGS results can be digested In-silico, PFGE and WGS data are being compared separately.
Methodology: To link results of both methods, we describe a new image analysis algorithm that enables identification of how many DNA fragments comigrate during PFGE. We built a database that compares results of the previously mentioned algorithm to In-silico obtained digestion models (from WGS). Reliability of the image analysis algorithm was also assessed In-silico using novel computer simulation approach. From WGS, 1,816 digestion models (DMs) were obtained as recommended by PulseNet international. Simulation codes were designed to predict PFGE profiles when DMs are separated at 5% PFGE resolution in addition to expected co-migration levels.
Results: PFGE simulation has shown that about 35% of DNA fragments co-migrate at 5% PFGE resolution. Similar result was obtained when wet-lab PFGE profiles were analyzed using image analysis algorithm mentioned earlier. In terms of number of PFGE typable DNA fragments, 45,517 were typable (representing 46.54% out of 97,801). Previously mentioned typable fragments (in terms of typable sizes) comprised 91.24% of the sum of nucleotides of all chromosomes tested (7.24 billion bp). However, significant variations were shown within and between different digestion protocols. When image analysis results were compared to DMs, results returned by geltowgs.uofk.edu database revealed reasonable relatedness (Dice coefficient of variation was 0.44) to the most related DM.
Conclusion:Identification of comigration levels will reveal the third dimension of PFGE profiles. This will provide a better way for evaluating isolate relationships. Linking old PFGE results to WGS by means of simulation demonstrated here will provide a chance to link hundreds of thousands of PFGE epidemiological data accumulated during the last 24 years to the new WGS era. Evaluation of population dynamics of pathogenic bacteria will be deeper through place and time. Selection of restriction enzymes for PFGE typing will have a powerful In-silico evaluation tool.
Keywords
Outbreak Investigations, PFGE, Pixel Density, WGS, Numerical Modeling, Simulation Algorithms, PulseNet International, Bioinformatics Database.
Nonstandard Abbreviations
DM; digestion model, BS; band size, PD; pixel density, SFB; single-fragment PFGE band, FCM; factor of co-migration, OPD; observed pixel density, EPD; expected pixel density, CCT; critical co-migration threshold, FCM-ECSB; factor of comigration based on exponential correlation between singlefragment bands and their pixel densities, PTS; percentage of typable size, NTB; number of typable bands.
Abstract
Background: Standard protocols for Pulsed-field gel electrophoresis (PFGE) were adopted and being used in a global scale for surveillance of many bacterial food-borne diseases. Matched PFGE bands are considered according to values of retention factors (rF) regardless of co-migration of different DNA fragments (having equal or very close molecular weight). Molecular epidemiology is turning toward whole genome sequencing (WGS), WGS results are compared using different DNA sequence alignment methods. Although, WGS results can be digested In-silico, PFGE and WGS data are being compared separately.
Methodology: To link results of both methods, we describe a new image analysis algorithm that enables identification of how many DNA fragments comigrate during PFGE. We built a database that compares results of the previously mentioned algorithm to In-silico obtained digestion models (from WGS). Reliability of the image analysis algorithm was also assessed In-silico using novel computer simulation approach. From WGS, 1,816 digestion models (DMs) were obtained as recommended by PulseNet international. Simulation codes were designed to predict PFGE profiles when DMs are separated at 5% PFGE resolution in addition to expected co-migration levels.
Results: PFGE simulation has shown that about 35% of DNA fragments co-migrate at 5% PFGE resolution. Similar result was obtained when wet-lab PFGE profiles were analyzed using image analysis algorithm mentioned earlier. In terms of number of PFGE typable DNA fragments, 45,517 were typable (representing 46.54% out of 97,801). Previously mentioned typable fragments (in terms of typable sizes) comprised 91.24% of the sum of nucleotides of all chromosomes tested (7.24 billion bp). However, significant variations were shown within and between different digestion protocols. When image analysis results were compared to DMs, results returned by geltowgs.uofk.edu database revealed reasonable relatedness (Dice coefficient of variation was 0.44) to the most related DM.
Conclusion:Identification of comigration levels will reveal the third dimension of PFGE profiles. This will provide a better way for evaluating isolate relationships. Linking old PFGE results to WGS by means of simulation demonstrated here will provide a chance to link hundreds of thousands of PFGE epidemiological data accumulated during the last 24 years to the new WGS era. Evaluation of population dynamics of pathogenic bacteria will be deeper through place and time. Selection of restriction enzymes for PFGE typing will have a powerful In-silico evaluation tool.
Keywords
Outbreak Investigations, PFGE, Pixel Density, WGS, Numerical Modeling, Simulation Algorithms, PulseNet International, Bioinformatics Database.
Nonstandard Abbreviations
DM; digestion model, BS; band size, PD; pixel density, SFB; single-fragment PFGE band, FCM; factor of co-migration, OPD; observed pixel density, EPD; expected pixel density, CCT; critical co-migration threshold, FCM-ECSB; factor of comigration based on exponential correlation between singlefragment bands and their pixel densities, PTS; percentage of typable size, NTB; number of typable bands.
Introduction
Pulsed-field gel electrophoresis (PFGE) is a form of agarose gel electrophoresis used to separate large DNA fragments of bacterial chromosomes [1]. Such large DNA fragments are obtained using restriction enzymes that have a rare recognition sequence across bacterial genome of interest [1]. Consequently, these fragments are generated in few numbers [2,3]. Plasmid contamination is regarded as false positive bands [4,5]. DNA methylation was found to result in false negative PFGE profiles for the enzyme SmaI [6]. Conventional agarose gel electrophoresis resolve a maximum band size of 40-50 kbp [7]. PFGE on the other hand is capable of resolving fragments up to 2 Mbp in size [8]. PFGE has shown exceptional reliability for bacterial strain typing [9]. Briefly, a PFGE protocol includes the following steps; genomic DNA of bacterial isolates is extracted in a gel plug, digested by the enzyme and resolved in low temperaturemelting agarose gel using counter-clamp homogenous field gel electrophoresis (CHEF). Ethidium bromide is used to visualize resolved fragments [9]. Resolution of CHEF was found to range from 10 to 5%. That means at best conditions DNA fragments differ by lt;5% will resolve within a single PFGE band (a phenomenon known as fragment comigration) [10,11]. A molecular weight marker is run to calculate retention factors (rFs) and DNA band sizes (BS) of bacterial isolates under investigation [12]. The optimum number of bands for proper final conclusions is more than ten and less than 30 band [13,14]. Although PFGE refers to other gel electrophoresis methods including field-inversion gel electrophoresis (FIGE) [15] the terms PFGE is being used as a synonymous to CHEF [16]. PulseNet International (PNI) is a global network of laboratories dedicated to real time surveillance and outbreak investigations using several standardized DNA based methods. Their methods include, but not only limited to PFGE and WGS. Several PFGE protocols were adopted for typing chromosomes of some pathogenic bacteria species in order to obtain comparable results at national and international levels [17]. PNI also standardized protocols for WGS [18].
A PFGE profile is not always pure DNA fragments. Artifact bands may appear across digestion profiles due to poor washing of extraction plugs. Incomplete digestion also results in false-positive bands, both artifacts are known as ghost bands. On the other hand, DNA co-migration results in bands with high pixel densities (PDs) [19]. Band intensity profiles are affected by the quality of Ethidium bromide staining and initial cell concentrations which is crucial for both; clearly visible bands across the same lane and less intensity differences between different lanes [13]. Comparison of PFGE fingerprints of bacterial isolates is based on the concept of position tolerance; bands that fall within ± 0.015 value of retention factor (rF) are considered a match [14]. In other words; a band exists or none exists within the range of tolerance of another one. That match is considered regardless of co-migration of different DNA fragments (difference in their lengths is too small to be resolved using CHEF) [14].
Computer-assisted analysis of PFGE images helps investigators to numerically express genetic relationships between isolates based on Dice coefficient of variation. Genetic relatedness of different isolates is graphically represented in a hierarchical clustering similarity tree using un-weighted pair group method with arithmetic averages (UPGMA) [20]. An exponential correlation was observed between DNA band sizes and their corresponding pixel densities across PFGE lanes [16]. An algorithm was developed by Warner and Onderdonk to consider pixel densities of common bands as comparison parameter for PFGE profiles. Their algorithm was based on standardized trace quantity (STCs) which shows differences in pixel densities of common bands. STCs indicate co-migration, but number of co-migrated fragments remained unknown [19].
Whole genome sequencing (WGS) is among the list of PulseNet international for typing methods [21]. WGS includes chromosomal and plasmid DNA in which the entire DNA content of the bacterial isolate is decoded. Different approaches for sequence alignment include extended multilocus sequence typing (MLST), k-mers and single nucleotide polymorphisms (SNP) [18]. Unlike PFGE, WGS provide more valuable details about antibiotic resistance, virulence associated mutations and accurate species and strain identification. PNI is turning toward using WGS instead of PFGE and multi-locus variable number tandem repeats analysis (MLVA) [18].
Genetic variations resulting in DNA fragments having < 5% difference in size remain hidden when comparison is based on position tolerance. In addition to false positive bands (ghosts). In our opinion, the two mentioned problems occur because band intensity profile is not being taken into account. Results of PFGE and WGS are still being compared separately [22]. The obvious reason is that comparisons are based on rF values not DNA band size. Development of PFGE protocols for different bacterial species is being done by wet-lab PFGE profiling using different restriction enzymes. Although restriction enzyme selection is being done based on WGS data, a simulation of PFGE separation that enable prediction of the profile including co-migration levels is not available. Percentage of PFGE typable size to total chromosome size is not being taken into account in such experiments. Considering the fact that typable fragments are limited by the range of the DNA ladder, the ratio of the sum of typable to the sum of non-typable fragments for several enzymes reflects genetic variations shown by each enzyme across a single chromosome sequence.
In this document we tried to answer the following questions:
Q1. How to calculate number of co-migrated DNA fragments across a PFGE profile and what are possible limitations for such a method.
Q2. If co-migration is quantitatively identified, how to compare such results to In-silico obtained digestion profiles
(From WGS) considering the fact that PFGE band sizes are estimation based on DNA ladder’s band size vs. rF exponential equation.
Q3. How to predict a PFGE profiles that show co-migration levels from WGS sequences if an In-silico digestion profile is obtained.
Q4. If typable PFGE bands are only considered when they fall within the range of the DNA ladder, how much is the percentage from total chromosome size that the sum of typable fragments represents.
If optimum number for proper conclusions is from 10 to30, how to evaluate each digestion protocol taking these parameters into account.
Methodology
Calculating factor of co-migration for S. enterica serotype Braenderup (strain H9812)
The correlation between band sizes and their corresponding pixel densities was reported to be exponential [23]. This finding is the cornerstone of the entire method upon which we made the following assumptions: A. In theory, a highly significant correlation coefficient (R2>0.99) can be obtained under the following conditions: a. complete digestion by the enzyme is granted. B. Highly pure DNA is extracted within gel plugs. C. all resolved DNA bands represent a single DNA chromosomal fragment (SFB) (or the same number of co-migrated fragments). D. High quality Ethidium bromide staining is granted (saturation of DNA content of each band by the dye).
Based on the previously mentioned assumptions we suggest that: a\ in case of multiple levels of co-migrated and single-fragment bands occurring across a single PFGE profile, correlation coefficient of exponential equation of band sizes vs. pixel densities will be reduced to a degree proportionate to mentioned levels of co-migrations. b\ in case of analyzing a PFGE profile that have an optimum number of bands (10 to 30 bands), too high (co-migration) and too low (ghosts) values of pixel densities can be removed to have an equation with R2 value =>0.98 (only SFBs will remain). The main guideline for identifying such ‘odd’ fragments is to take into account that pixel density (PD) should reduce as band size do.
Accordingly if a band size shows a PD that is higher than that of the larger fragment, then it represents comigration and it should be removed. The exception to this rule is the presence of ghost bands. Ghosts may show a significantly low PD that my miss lead the entire calculation. c\ by re-creating a polynomial fit and checking values of R2, a significantly high R2 value can be obtained (0.98 or more.). d\ by denotation of band sizes of the entire profile into the resulting high-R2 valued equation, expected pixel densities calculated represents the assumption that all fragment sizes represents a single DNA fragment (a matrix of three columns is obtained at this point). e\ by dividing observed pixel densities (provided by image analysis software) by their expected ones, a proximate number of co-migrated DNA fragments can be obtained. Since integer number is expected, truncation of Observed PD/Expected PD is necessary. This suggested parameter was named factor of co-migration (FCM).
MEPD = MR −MOV
While MEPD+ MOV = MR
Where MEPD ; is the two-columns matrix that have R2 value> 0.98 for its correlation equation and from which expected pixel densities will be calculated, MR is the matrix of raw data and MOV is the matrix of odd values of pixel densities.
In order to test the above mentioned method, a metaanalysis for the widely adopted DNA ladder suggested by Hunter and here team [12] was done from some previously published PFGE results [12,23,24]. We focused on the DNA ladder suggested by Hunter and her team [12] because it run under different conditions across the literature cited (18 different lanes in total). Screen shots for each PFGE image was obtained. Images were saved in .jpg format. Images were imported to GelAnalyzer2010 [25]. Gel default colors were set to black DNA bands on white background. Lanes and bands were defined automatically by the software and in some cases, manual modifications were necessary (more frequently for band assignment). Lanes indicated by authors to show XbaI digestion profiles of S. enterica serotype Braenderup (strain H9812) where set as DNA ladder for the software. Each band was assigned with its corresponding length in base-pairs. Pixel densities were calculated automatically by the software. Image analysis results were transferred to Paleontological Statistics (PAST) software package version 4.0. Correlation equation of MEPD matrix was created. Denotations, obtaining values of observed/Expected PDs and truncation to obtain FCMs were all done using Microsoft Office Excel 2007 software package. Mean ± SD and median were calculated from the entire dataset for each band size to get a final FCM-ECSB result using PAST statistics [26]. The entire image analysis algorithm described was named factor of co-migration from exponential correlation of single-fragment bands and PD (FCM-ECSB). Supplementary material 1 (S1) is a video file showing a complete demonstration for the entire FCM-ECSB method (stream online here).
In-silico digestion of whole chromosome sequences
Chromosomal sequences in this study were chosen from the NCBI Genome database, regardless of randomization or any statistical method for selection. NCBI Genome database was searched for each bacterial species (scientific name + complete genome) that has a standard protocol adopted by PulseNet international. In addition, chromosome sequences for K. pneumonia (which is yet to have a standard protocol) were also included. Total number of whole chromosome sequences was 1,194 (Supplementary material 2 (S2)) shows NCBI GeneBank accession numbers, bacterial species and strain of whole chromosome sequences in this study. Since PFGE is designed for typing chromosomes, plasmid interference is regarded as false positives [4,27]. From table of results returned by NCBI genome database, Plasmids, contiguous and scaffold sequences were excluded. The table of result set was downloaded from the NCBI website in comma separated values file (.csv format). From Replicons column (GeneBank accession numbers) of the result set, Chromosomal sequences were downloaded from the NCBI sequence database in FASTA format. Fragment length for each chromosome were generated considering whether the chromosome is linear or circular using DNADynamo™ software (Blue Tractor Software, North Wales, UK) version 3.4 in default settings. Recommended restriction enzymes for each species were set in separate enzyme boxes (required by the software). Digestion results (numerical values of fragment sizes in base-pairs) were exported to text file format (.txt file extension). Text files were imported to Microsoft office Excel 2007 and refined. Refinement process included removing all metadata for each digestion model except accession numbers (keeping fragment sizes). Digestion result columns (DNA fragment sizes in base-pairs) were transposed into column with accession numbers at the first row. Microsoft Excel files were imported to Microsoft SQL server™ (2014) using SQL server import and export wizard. Data were saved in permanent SQL server database tables. Data are stored in columns representing the length of each DNA fragment for each chromosome sequence in descending order. NCBI GeneBank accession numbers were assigned as a unique identifier (column names) for each digestion model. For data integrity and accurate comparison purposes, table names indicate bacterial species and the restriction enzyme used. Tables of result sets downloaded from NCBI genome database were also imported to the SQL server database to retrieve meta-data from. SQL algorithms were written to compare data uploaded to the system with all models of a specific bacterial species that were generated using the same restriction enzyme and analyzed using the described FCM-ECSB method. Some of the models were used for simulation of PFGE and the assessment of FCM-ECSB method which were shown in this article.
GelToWGS database algorithms
The database contains 2,420 digestion models. All algorithms were designed to predict number of matched fragments if each DM is run under the same PFGE conditions as test data. To run such simulation, database server is configured to require four parameters from the end user; FCM-ECSB results (Wet-lab PFGE estimated band sizes and corresponding FCMs), which should be uploaded in MS Excel (.xlsx file format), critical co-migration threshold (CCT); it represents resolution quality of PFGE (reported to range from 5 to 10%). Error resulted from running condition (indicated by correlation coefficient of band size vs. rF correlation). Since band sizes estimated from a PFGE profile cannot be treated as exact numeric values, in contrast to Insilico obtained DMs it is almost impossible to get an exact match. Building on this assumption, upper and lower limits for uploaded band size columns are automatically generated. They are filled with data based on a total estimation error (TEE). A final comparison template is required to represent two numbers for each PFGE fragment distanced by a range equals to selected CCT+ DNA ladder error. The following equations put theory into a mathematical form:
Where TEE; is the total estimation error, CCT; critical co-migration threshold, R2; correlation coefficient of DNA ladder’s BS vs. rF correlation, 1; represent 100% R2 value. Calculations divided by 2 because to values will be calculated.
And
Where UL; is the upper limits. LL; is the lower limits. BS; is a single-column matrix representing wet-lab PFGE band size estimations (uploaded by the end user), TEE; total estimation error.
GelToWGS comparison algorithm will scan each model and count the number of fragments from the model that falls within each range of upper and lower limits across the entire submitted data compared to each digestion model separately. Fragment length is from the genome models, while upper and lower limits are from the image analysis.
When comparing FCMs (from test) to the count (from each model), there are three possibilities: A. Test greater than query; in this case, matched bands = query (the count) B. Test is less than query; matched bands = FCM. C- Equal count and FCM; query count will be considered as matched bands. The computer will calculate the sum of matched bands. Dice coefficient of variation will be calculated to reveal relatedness to each model. Finally, percentage of similarity for both, test and query will be calculated according to the equations:
Where PST; is the percentage of similarity to test. MB; matched bands. FCM; is the factor of co-migration.
Where PSQ; is the percentage of similarity to query. MB; matched bands. NTB; is the number of typable fragments (from query) between the biggest and the smallest band size (from PFGE).
The algorithms will also retrieve genome metadata using NCBI accession numbers as a unique identifier that correspond each digestion model. Previously mentioned FCM-ECSB results of S. enterica serotype Braenderup strain H9812 (mean values of FCMs truncated to the nearest integer values) where uploaded to the system alongside the following values; 5.2% CCT and 0.002 error of DNA ladder. Data were compared to 420 whole chromosome sequences of S. enterica digested by XbaI restriction enzyme (In-silico generated PFGE profiles).
PFGE simulation (WGSToGel)
The target is to evaluate Possibilities for DNA fragments to resolve into single bands and quantitative assessment of co-migration possibilities. Based on the conclusion made by Struelens and his colleagues that DNA fragment comigration occurs if the percentage of difference between two or more fragments is in the range of 5-10% [9,10]. The same 5% co-migration threshold was adopted by Singer and colleagues [4] to simulate PFGE profiles. We calculated Dice coefficient %age as the difference between a single fragment and the following six fragments after descending order. Mathematically, calculations can be expressed as two parts algorithms:
Where Sim%age; is a single row matrix (x 6 columns) that represent % age of Dice difference between a single DNA fragment and the following six fragments. F; is the fragments size while n; is the integer number that represents the order of the corresponding fragment size after descending order of the entire digestion profile.
Typable fragments are defined as DNA fragments having sizes within the range of Hunters DNA ladder (20.5 kbp to 1.135 Mbp). Any DNA fragment outside this is automatically excluded from all simulation process. For calculating the Sim%age values for a complete In-silico obtained digestion profile, the same six columns matrix will be created for each typable DNA fragment size. Accordingly, number of rows will equal to typable fragments for each digestion profile, the following algorithm was executed separately for each digestion profile:
Where SM; is the simulation matrix for fragment lengths of a single digestion profile within the range of 20.5 kpb to 1.135 mega base pair. Sim%age; is the equation of single row matrix mentioned earlier. F; fragment size n; is the integer number corresponding the fragment size (F and n are the required parameters for Sim%age equation).
Previously described calculations were made to a total sample size of 1,816 In-silico obtained digestion profiles. Total number of typable fragments is 45,517.
Band size and FCM simulation
The target was to predict a matrix representing PFGE profile consisting of two columns; band size and corresponding FCM simulations. This algorithm was designed to scan previously described SM matrix and assigning values for BS and FCM based on the following cases:
The difference between two fragments > 5%: the algorithm will give simulated band size the same value of In-silico obtained fragment size. FCM is set to 1 (indicating the expected PFGE band is a single-fragment band (SFB)). Mathematically, the process can be expressed a follow:
And
Where FS; is the In-silico obtained fragment size, dif; is Dice percentage of difference (calculated six times), SM; simulation matrix, BSsim; expected band size, 1; FCMsim value that indicate no co-migration occurs.
The difference between two or more fragments <= 5: in this case, the algorithm sets simulated band size as the average of co-migrated fragments. While simulated FCM is their corresponding number. The following equations sets mentioned logic into mathematical form:
And
Where FS; is the In-silico obtained fragment size, dif; is Dice percentage of difference (calculated six times), SM; simulation matrix, BSsim; expected band size, n; order of fragment size, i; the number of fragments having <= 5% difference
Number of typable bands
According to the results of the previously described single and co-migrated bands, simulation algorithm was designed to perform two tasks; firstly, to calculate the total number of bands expected to be visible in actual PFGE assay (single or co-migrated). Secondly, to assign an evaluation rank based on the conclusions described by Van Belkum and colleagues which that the optimum number of bands for proper evaluation of PFGE fingerprints is more than ten and less than 30 [9,14]. Accordingly, the same range is ranked as “Optimum” by this algorithm. For models that does not satisfy the cited definition; results were arbitrarily clustered into four different ranks; When number of bands is more than 30; we assigned the label ‘Too much bands’ and when it range from 9 to five, then the category is “Few bands”. The category ‘Very few bands’ is assigned when the number of bands is four or three bands. Models that show only one or two bands were labeled as “Non-typable”. This simulation was separately executed for each digestion model.
Typable size of PFGE to total chromosome size
PFGE typable size is defined as the percentage of the sum of DNA fragments within the range of 1.135 Mbp to 20.5 kbp to the total chromosome size. SQL queries were written to calculate the sum of fragment sizes that satisfy the definition mentioned earlier and calculate the percentage to the whole chromosome size for each model according to the equation:
Where: PTS is percentage of typable size. FS; fragment sizes and TCS; is the total chromosome size
Statistical analysis
FCM-ECSB: Polynomial correlation (order 1) between band sizes and both; rFs and PDs was done using PAST statistical package [26]. Denotations to calculate EPDs, OPD/EPD and calculating FCMs were done using Microsoft Office Excel 2007. Univariate statistics for Hunters ladder table 1 which include; means ± SD, medians, and p-values were also done using PAST statistics software package [26]. GelToWGS statistics: Dice coefficient of variation is automatically calculated by database server for matched fragments between test data and each digestion model separately. WGSToGel simulations: NTBs and PTSs ranks described earlier were implemented to simplify intended statistics (percentages of NTB categories for each PTS, total PTS, total NTBs and the same parameters for each digestion model). All statistics were calculated using customized SQL scripts to extract and summarize statistics shown in relevant sections. Scripts were run on supplementary material 4 (S4) table.
Results
FCM-ECSB results of Xba1 digestion of S. enterica serotype Braenderup (Strain H9812)
Since PFGE of whole genome of S. enterica serotype Braenderup (Strain H9812) digested by XbaI is suggested by Hunter and here team (12) is widely adopted as DNA ladder for bacterial PFGE typing, we sometimes refer to it as Hunter’s DNA ladder. FCM-ECSB results of Hunter’s DNA ladder were found to be affected by different electrophoresis conditions. Table 1 shows expected number of DNA fragments represented by each band of the ladder. Columns under the heading “FCM-ECSB results” shows descending order of Hunter’s ladder band sizes in base-pairs from larger to smaller (1135000, 668900, 452700, 398400, 336500, 310100, 244400, 216900, 173400, 167100, 138900, 104500, 78200, 54700, 33300, 28800 and 20500). Rows show FCM-ECSB results for each lane indicated by the authors to show Hunter’s DNA ladder. Mean and median of FCM-ECSB results of Hunter’s DNA ladder suggest that out of the 17 PFGE bands; 15 bands represent single DNA fragment. They include bands number 1 to 12, 14 and 16 and 17. Bands number 13 includes two different DNA fragments while band number 15 includes three different co-migrated DNA fragments. Deviations from the mean values occurred in 40 bands (≈13%) out of the whole dataset of 302 (17 PFGE band across 18 lanes of the same Hunter’s ladder. 4 bands did not separate in 2 lanes. Consequently, the total is 17*18-4 = 302). When considering standard deviations across band sizes of the Hunter’s DNA ladder; the highest SD (±1.2) of number of DNA fragments in each band was shown by band number 15 which we concluded that it represents three different co-migrated fragments. SD for other bands ranged from ±0.0 to ±0.5 DNA fragment for each band. We evaluated PFGE profiles based on correlations between band sizes and rF values on one hand and BS and pixel densities on the other; unlike other criteria already adopted in the literature. The results have shown that correlation coefficient of the exponential correlation between BS and rF were highly significant (more than 0.99 with p-values ranging from 1.9566E-05 to 6.3007E-06) and slightly lower between BSs and PDs (between 0.79 and 0.90 with p-values ranging from 5.47E-08 to 1.08E-08) in PFGE gels those have 100% FCM matches with medians (same mean values when truncated to integer values); namely figure 1 (c) reported by Han and colleagues (Table 1; rows #4 to #7). The same running conditions were reported to be optimum for typing chromosomes of K. pneumonia by the authors. Similar r2 values were found in the work reported by Hunter and her colleagues in running conditions recommended for typing chromosomes of both L. monocytogenes and E. coli and Shigella. Two PFGE bands for Hunter’s ladder run under protocols of L. monocytogenes and E. coli-Shigella have shown 2 co-migrated DNA fragments while compared to mean values, namely; band #1 and #2 respectively (Table 1, rows #9 and #10). Hunter results for Salmonella protocol have shown two deviations in band #8 and #15. Both deviations were over estimations; 2 and 4 for bands #8 and #15 respectively Table 1 row #9. The exception in Hunter’s work is that bands number 9 and 10 were not separated in gels run under protocols of E. coli-Shigella and Salmonella. For electrophoresis parameters concluded by Han and colleagues as non-optimal; they both showed 32 deviations from the mean (≈10% of deviated FCM estimations). Our estimation criteria mentioned above have shown that R2 of BS vs. rF for electrophoresis parameters (EP) a and b were tightly around 0.974 (p-value ranged from 1.90E-06 to 1.57E-07) and 0.959 (p-value ranged from 2.2309E-05 to 1.6953E-05) for EP a and b respectively.
Our FCM-ECSB results showed that separation quality can be evaluated based on correlation between BSs and rFs. Table 1 columns under the header “Raw gel parameters”.
GelToWGS comparisons of Hunter’s DNA ladder to XbaI-digested S. enterica chromosomes
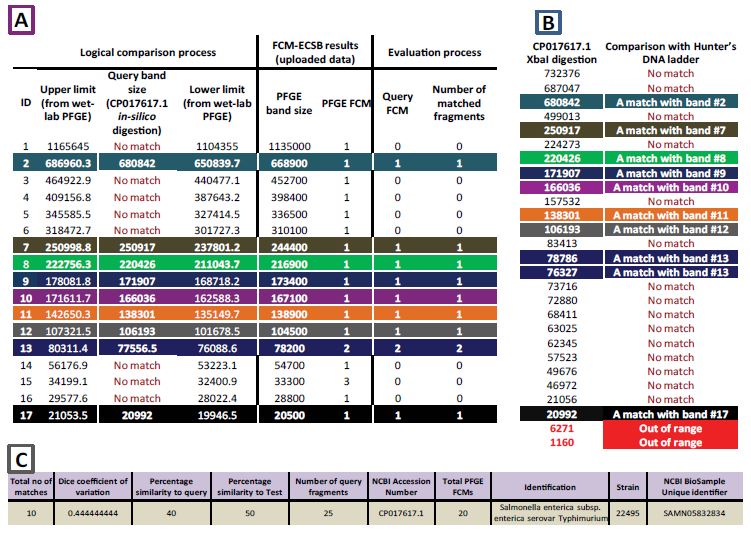
Here, we tried to answer the question “Is it possible to link PFGE results to digestion profiles derived In-silico from WGS?” We found that out of the 420 digestion models (derived from whole chromosome DNA sequences digested In-silico by Xba1 restriction enzyme) which Hunter’s ladder FCMECSB results were compared to, 197 (46.90%) DM showed at least one DNA fragment match with the Hunter’s DNA ladder. Total number of typable DNA fragments across the previously mentioned 197 DM was 7,600 typable fragment, out of this figure; matches with Hunter’s DNA ladder were 1,461 (19.22%) match. Number of matched fragments ranged from 11 to 4 matched fragments per DM. Consequently, no epidemiologically related isolate was shown. XbaI digestion profile of S. enterica subsp. enterica serovar Typhimurium (strain 22495) whole chromosome sequence has shown 10 matches and the highest value of Dice coefficient of variation (0.444). Number of typable query fragments of this strain is 25. In contrast to strain SL1344RX of the same serovar which showed 11 matches, that number of query fragments of strain SL1344RX is 51 typable DNA fragment. Percentages of similarities to query for both strains 22495 and SL1344RX are 40% and 21% respectively. Figure 1 shows details of GelToWGS comparison algorithm upon which previously mentioned conclusions were made. Comparison showed that out of the 17 bands of the Hunter’s DNA ladder which represent 20 different DNA fragments. On the other hand, n-silico obtained XbaI digestion profile of S. enterica strain 22495 (GeneBank accession number CP17617.1) resulted in 27 DNA fragments out of this figure; two DNA fragments had less than 20.5 kbp (not typable by PFGE). The remaining 25 showed a single match with Hunter’s DNA ladder (PFGE band #2, #7 to #12 and #17). And two matches were found with band #13 (Two co-migrated fragments). Supplementary material 3 (S3) shows the details of conclusions mentioned above.
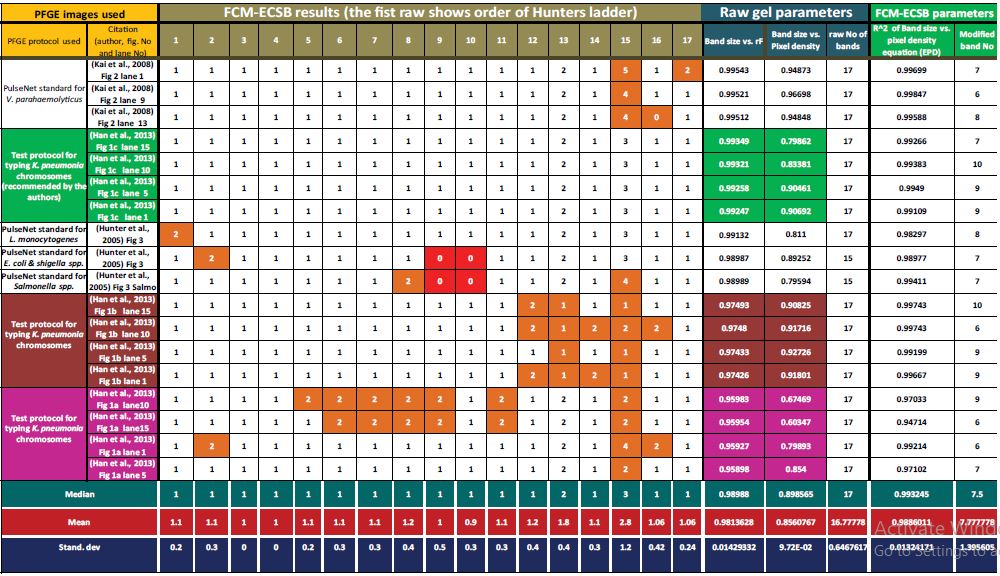
Table1: Meta-analysis of XbaI digestion of S. enterica serotype Braenderup (strain H9812) profiles using FCM-ECSB image analysis algorithm. The table shows number of DNA fragments represented by each PFGE band across XbaI digestion profile of S. enterica serotype Braenderup (strain H9812) across 18 different lanesrun under different electrophoresis conditions Columns under the heading “FCM-ECSB results” shows descending order of Hunter’s ladder band sizes in base-pairs from larger to smaller (1135000, 668900, 452700, 398400, 336500, 310100, 244400, 216900, 173400, 167100, 138900, 104500, 78200, 54700, 33300, 28800 and 20500). The first column from left shows citations for each PFGE image (figure numbers) and order of Hunter’s DNA ladders lanes from left to right across gel image. Columns under header “PFGE bands” show order of each band of Hunters DNA ladder from the largest band size (1,135 Mbp) to the smallest (0.0205 Mbp. Values highlighted in brown are deviated from truncated values of the average (same as median values). Values highlighted in red were bands not separated (no band size is assigned by the authors). Values under column header “Raw gel parameters” show correlation coefficient of exponential equation of band size vs. retention factor (rF) calculated by GelAnalyzer2010image analysis software. Column named “Band size vs. pixel density” Shows correlation coefficient of polynomial fit created for the entire PFGE profile (column named “raw number of bands” shows total number of Hunter’s DNA ladder bands assigned by each author) the correlation between BS and PD was reported to be exponential, but deviations from high R2 is due to co-migration of different DNA fragments. Columns under the header “FCM-ECSB parameters” shows parameters of modified BS vs. PD equation used to calculate expected pixel densities for each band size assuming that selected values represents single-fragment PFGE bands shows how many PFGE bands were chosen to create a polynomial fit between their band sizes and pixel densities to obtain a correlation equation that has a value of R2 shown within column named “R2 values of BS vs. PD equation”. PD values calculated by GelAnalyzer2010 software were divided by expected PDs calculated from FCM-ECSB equation to obtain approximate number of DNA fragments in each band. Since an integer number is expected, values were truncated to the nearest integer value. Results show that 40 band out of 302 (13.24%) deviated from average number of DNA fragments for each band (mean and median values at the bottom of the table).
Based on the previously mentioned conclusions, the main logic of GelToWGS algorithms; upper and lower limits of PFGE band size estimations based on PFGE resolution and DNA ladder’s error allowed comparing the exact numeric values of In-silico digestions to PFGE band size estimations.
Prediction of PFGE profiles from In-silico digestions according to PulseNet international typing protocols (overall simulation results)
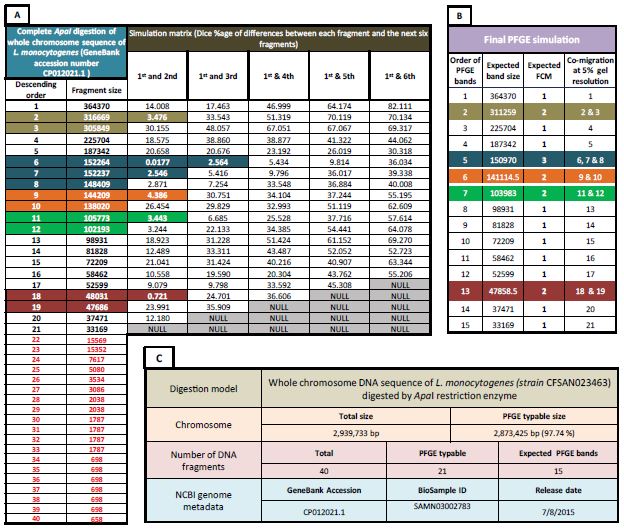
The target is to obtain the expected FCM-ECSB results if the same isolates those have their chromosome sequenced have also been subjected to PFGE using restriction enzymes recommended by PNI. The following results show overall simulation (regardless of bacterial species or digestion protocol). Among 1,816 predicted FCM-ECSB; in terms of size, typable fragments were found to represent 91.24% out of about 7.24 billion bp which represents the sum of nucleotides of whole chromosome sequences tested. In terms of number of chromosomal DNA fragments the total was 97,801. Typable DNA fragments comprised 45,517 fragments (46.54% from total). Our results show that fragment sizes having < 20.5 kbp are actually more than typable ones (generally speaking, the sum of length of such fragments comprised a small fraction of each chromosome tested). Among typable fragments; DNA co-migration reduced number of typable fragments (to expected number of PFGE bands) to 29,430 (35.34% of typable DNA fragments co-migrate) when PFGE resolution is 5%. Singlefragment expected PFGE bands comprised 18,225 PFGE bands (61.93% of expected bands). While two co-migrated fragments comprised 7,809 PFGE band which about a quarter of expected PFGE bands (26.53%). Co-migration of three DNA fragments is represented by 2,400 expected PFGE bands (8.15%). Fragment co-migration of 4, 5 or 6 different DNA fragments comprised only 3.39%. Supplementary material 4 (S4) shows the complete simulation results. Figure 2 shows a detailed demonstration of how simulation results upon which above conclusions were made. It shows how a PFGE profile is predicted for whole chromosome sequence of L. monocytogenes Strain CFSAN023463 (NCBI GeneBank accession number CP012021.1) when it is digested by ApaI restriction enzyme.
Figure 1:GelToWGS database comparison of Hunter’s DNA ladder to XbaI-digested S. enterica chromosome sequence (NCBI GeneBank accession number CP17617.1). The three tables above show comparisons and evaluation conclusion created by GelToWGS database server when comparing FCM-ECSB image analysis results to digestion profiles of whole chromosome sequences (In-silico driven). PFGE digestion profile of S. enterica serovar Braenderup (strain H9812 digested by XbaI restriction enzyme) was analyzed using FCM-ECSB algorithm in order to reveal number of co-migrated DNA fragments within each PFGE band. FCM-ECSB results (band sizes and corresponding FCMs) where uploaded to the system (analysis parameters: 5.4% critical co-migration and 0.008 Hunter’s DNA ladder error). Uploaded data was compared to In-silico driven XbaI digestion profiles of some S. enterica whole chromosome sequences (420 different digestion profiles in total). S. enterica subsp. enterica serovar typhimurium strain 22495 (GeneBank accession number CP017617.1) has shown the highest number of matched DNA fragments (10). Table A: detailed comparison results showing In-silico driven DNA fragment sizes from CP017617.1 those fall within ranges (upper and lower limits at a distance of about 5%) of actual PFGE band sizes. Matching fragment sizes are indicated by their values and colors (the same as table B). While ‘No match’ indicate that XbaI digested CP017617.1 does not include a fragment size at that range. Columns under the tag ‘Evaluation process’ shows how total matched fragments are considered. Table B: Complete XbaI digestion profile of CP017617.1 showing matched (colored) and non-matching (‘No match’)DNA fragment sizes within upper and lower limits of table A. Fragment sizes in red falls outside the typable size of the Hunter’s DNA ladder, consequently they are excluded from Dice Coefficient calculations. Table C: shows typability conclusions and metadata of chromosome sequences within NCBI database.
Variations of co-migration levels among different bacterial species and different PFGE protocols recommended by PNI (different restriction enzymes for each species)
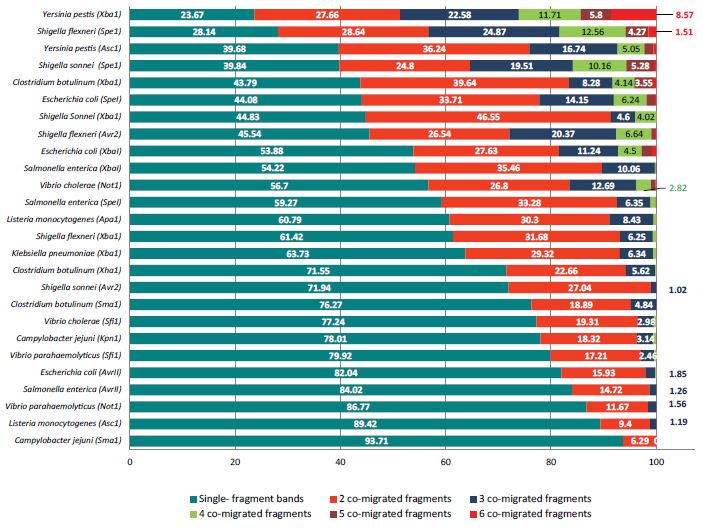
When each digestion model is considered, significant variation were shown in terms of total co-migration levels. In 18 DMs out of the 26 had single-fragment PFGE bands comprise more than 50%. The rest (8 DMs) had singlefragment bands comprised less than 50%. High percentage of SFBs was shown by C. jejuni (SmaI) and L. monocytogenes (AscI) by 93.71% and 89.24% respectively while, Y. pestis XbaI and S. fluxineri showed SFB by 23.67% and 28.14% respectively. Y. pestis XbaI has also shown all co-migration levels tested represented by considerable fractions. The highest percentage of double-fragment bands was shown by C. botulinum XbaI and S. enterica SpeI by 39.64% and 35.46% respectively. Figure 3 Shows details of each PNI typing protocol.
Figure 2: PFGE simulation that show expected PFGE band sizes and corresponding factors of co-migration (FCMs) if the whole chromosome sequence of L. monocytogenes (Strain CFSAN023463) is digested by ApaI restriction enzyme and run under conditions grant that chromosomal fragments differ by more than 5% are separated. Table A: the first two columns; shows the complete In-silico obtained digestion profile of the mentioned DNA sequence. Fragments shown are in descending order of size regardless of position in the chromosome. Data were obtained using DNADynamo bioinformatics software package. These data simulates digested chromosome sequence in PFGE gel plug before separation. Fragments starting from 22 to 40 are less than 20.5 kbp which is the smallest band size in the widely adopted PFGE DNA ladder reported by S. Hunter and colleagues (values in red). Hence, these fragments were excluded from the simulation. Columns under header text “simulation matrix” show differences between each typable DNA fragment and the following 6 fragments. This difference was calculated as Dice percentage. It is simply calculated by multiplying the absolute subtraction values of each two DNA fragments by 2 and dividing the result by the sum of the two DNA fragments multiplied by 100. This matrix represents possibilities of how likely DNA fragments will co-migrate after PFGE. Factors that determines the final profile is the running distance and quality of running conditions. Table B: shows the final predicted PFGE profile if running conditions and distance were able to separate fragments differ by > 5%. Predictions were made based on simulation matrix (Table A). Colored backgrounds correspond co-migrated DNA fragments across both tables (A and B). Table C: shows over all summaries for digestion profile and metadata of chromosomal sequence. NCBI BioSample ID shows epidemiological metadata.
Evaluation of PulseNet international PFGE typing protocols based on In-silico digestions of whole chromosome sequences
Since that development and adoption of PFGE typing protocols does not take into account the percentage of the sum of typable fragment to total chromosome size. It only depended on the number of bands shown by a given bacterial isolate when it is digested by several restriction enzymes [28]. We evaluated the relationship between percentage of typable size and the number of PFGE bands shown by each DM. Our results have shown that fragments representing a complete chromosome shown within the typable range of Hunter’s DNA ladder (1.1135 Mbp to 20.5 kbp) (i.e. 100% PTS) comprised 29 DMs (1.6%) of all digestion models of PFGE simulation (1,816). This category showed only optimum (10-30) and few bands (9-5) ranks. Digestion models in this category were dominated by SfiI digestions of V. parahaemolyticus (14 DMs), AvrII digestion of S. enterica (8 DMs). Number of DNA fragments ranged from 5-23 table 2 and supplementary material 4 (S4). Chromosomes covered by >95% (significantly high PTS) comprised more than three quarters of the entire dataset with 1,385 DM (76.27% from total). This PTS category showed all NTB ranks from optimum to non typable but optimum NTB category was the dominant with 1,225 DM (88% of this category) followed by few bands 103 (8%) table 2. Models that showed less than 5 DNA fragments comprised only 4%. Interestingly, non typable and Very few bands at this significantly high coverage were shown by 32 and 18 DM respectively table 2. All these models belong to C. jejuni SmaI digestion. Small chromosome size of this species is obviously the reason supplementary material 4 (S4). Chromosomes with high PTS (80-95%) were represented by 126 DM (6.94% of total). They also showed all NTB ranks but unlike significantly highly covered DM, 121 DM showed optimum NTBs (96%).
Figure 3: Evaluation of PulseNet international PFGE typing protocols. The graph shows expected percentages of DNA fragments co-migration and singlefragment PFGE bands for each digestion protocol when DNA fragments differ by >=5% were separated in PFGE gel. Simulation was performed after calculating percentage of differences between each fragment across In-silico generated digestion profiles and the next six fragments. The total sample size comprised 1,816 digestion models. Total number of DNA fragments of the entire dataset is 97,801. Among this figure; typable DNA fragments (TFs) (having sizes within the range of the widely adopted DNA ladder for PFGE suggested by S Hunter and her team 1.135 Mbp and 20.5 kbp) were 45,517 (46.54%). When typable fragments are separated using PFGE; the 45,517 will show 29,430 PFGE band. Accordingly, total DNA fragment co-migration comprises 16,087 PFGE band (35.34%). Results shown were derived from typable fragments defined earlier. Out of the 29,430 expected PFGE band; 18,225 (61.93 %) are FGE bands representing single DNA fragments. While 7,809 (26.53 %) were expected PFGE bands representing two different DNA fragments co-migrated. Triple-fragment expected PFGE bands comprised 2,400 bands (8.15%). Co-migration of 4 to 6 different DNA fragments comprised only 3.39%. Total levels of co-migration mentioned earlier are shown in details for each digestion model. It is obvious that these ratios differ greatly among chromosomes of different bacterial species and even when the same chromosome is digested by different restriction enzyme.
The majority of DMs showed this category is SpeI digestion of E. coli, S. sonni and S. fluxneri table 2.
In addition to NotI digestion of V. cholrae and XbaI digestions of Y. pestis. Chromosomes covered by 65-80% (moderately covered) were represented by 179 DM (9.86% from total). 73% of this PTS category showed few bands (9-5 DNA fragments) and the rest have shown optimum NTB. Interestingly, only three DMs show this PTS category which resulted from digestion by the restriction enzyme (AvrII) for both; E. coli and S. enterica. Only 4 DMs of C. botulinum were also shown this PTS category. Chromosomes covered by 50-65% (low coverage) comprised only 36 DM out of the entire sample size (1,816). This PTS category was found to be similar to moderately covered chromosomes in terms of NTB ranks. It also showed few bands (86%) and Optimum (14%) NTBs table 2. This PTS category was also dominated by AvrII digestion of E. coli and S. enterica chromosomes with only two DMs of L. monocytogenes (AscI). Poorly covered chromosomes (25-50%) are represented by only 17 DMs (the fewest PTS category). It showed three NTB ranks; optimum, few and very few bands. Unexpectedly with this poor PTS, non-typability is not shown. This PTS category is also dominated by AvrII DMs of E. coli and S. enterica. Chromosomes that show PFGE-typable fragments covering less than the quarter comprised 44 DMs (2.42% of total). As expected, this PTS category does not include optimum NTBs. In fact, non-typable chromosomes represent 30% of this PTS category. Very few bands comprised 15 DM (34%) and few bands included 16 DMs (36%). Very poorly covered chromosomes were shown by three DMs. It was dominated by C. botulimum (XbaI) followed by C. jejuni (SmaI) and a single DM of E. coli (AvrII). Table 2 shows a summary of previously mentioned conclusions and supplementary material 4 (S4) shows details of simulations of each single digestion model.
Discussion
This article is mainly dedicated to describing mathematical bases of suggested algorithms. And their relevance to both; PFGE images and in-silico obtained digestion models. Epidemiological or genetic relationships are not our priority. All described methods in this document do not provide ‘ready to use’ protocols to be adopted. They are simply suggestions those will need lots of experimental evaluation by future research. Here, we would like to summarize some limitations those may have affected our results in addition to some suggested evaluation guidelines for future research.
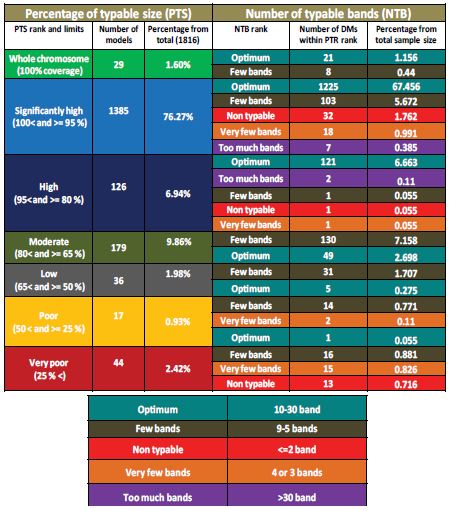
In-silico evaluation of currently used PFGE protocols in terms of percentage of typable size to total chromosome sizes (PTSs) and corresponding number of expected PFGE bands for each PTS range. Evaluation and simulation included chromosomal DNA fragments having sizes within the range of 1.135 to 0.205 Mbp and fragments differ by >5% are separated. Among a simulation dataset of 1,816 digestion profile, total number of fragments was 97,801. From this figure; 45,517 (46.54% from total) fragments were typable within the mentioned range. Furthermore, among the typable fragments; DNA fragments co-migration comprised 16,087 (35.34%). Hence, above conclusions were made based on total expected PFGE band comprises 29,430. Generally speaking, adopted PFGE protocols were found to cover major parts of chromosomes tested that; 77.87% have shown PTS coverage at >= 95% including 26 digestion model with 100% coverage. At these significantly high PTSs; number of expected PFGE bands is generally optimum. In contrast to low-PTS digestion models which showed low NTBs. Supplementary material 4 (S4) shows details of simulations of each single digestion model.
FCM-ECSB results of Hunter’s DNA ladder
Regarding our fundamental assumption that selected PFGE bands for EPD equation represent SFBs taking into account that if they were double or triple-fragment bands, they will result in a similar high r2 valued equation. Two evidences may support our claim; firstly, simulation results showed by XbaI digestion models of S. enterica chromosomes (70 DM in total), SFB comprised 841 expected PFGE bands out of 1551 (54.22%). NTB data mentioned earlier when combined with estimation of typable chromosome size calculated by the sum of band sizes multiplied by corresponding FCM of Hunter’s DNA ladder result in 4.7 Mbp (estimated typable size, not total chromosome size). This figure is close to the average of typable chromosome size of this digestion model (4.53 Mbp ± 381.8 kbp). But when assuming that Hunter’s ladder bands shows at least 2 DNA fragments (FCMs +1), PFGE typable size increased to 9.27 Mbp. This figure is too high even when compared to average of total chromosome size among our data (4.74 Mbp ± 129.5 kbp). When ignoring co-migration (supposing that each PFGE band is SFB), typable size will be 4.56 Mbp. We conclude that FCM-ECSB method may be evaluated based on calculating typable size of chromosome according to the mentioned method.
Table 3:Number of matches with each band of Hunter’s DNA ladder when its FCM-ESCB result was compared to 420 whole chromosome sequences of S. enterica digested by XbaI in-silico. Results below were shown by only 197 digestion model out of the total sample size. The rest of the sample size didn’t show any match at all. The first three columns simply show results of actual PFGE assay; order of each fragment indicated by the index, PFGE band size and factors of co-migration. Query matches show total number of matches shown for each band size of the marker while, actual matches result after comparing query matches with FCMs of the marker. These results reveal the common and the rare matched fragments with the marker across all XbaI digestion models of S. enterica chromosome sequences tested. Furthermore, it clearly show effects of co-migration when considering FCMs compared to ignoring it (query and actual matches).
| Index | PFGE band size | PFGE FCM | Query matches | Actual matches | Excluded due to comigration | %age of query matches | %age of actual matches |
|---|---|---|---|---|---|---|---|
| 1 | 1135000 | 1 | 1 | 1 | 0 | 0.043084877 | 0.062735257 |
| 2 | 668900 | 1 | 239 | 129 | 110 | 10.29728565 | 8.092848181 |
| 3 | 452700 | 1 | 18 | 16 | 2 | 0.77552779 | 1.003764115 |
| 4 | 398400 | 1 | 11 | 10 | 1 | 0.473933649 | 0.627352572 |
| 5 | 336500 | 1 | 18 | 14 | 4 | 0.77552779 | 0.878293601 |
| 6 | 310100 | 1 | 8 | 8 | 0 | 0.344679018 | 0.501882058 |
| 7 | 244400 | 1 | 182 | 176 | 6 | 7.841447652 | 11.04140527 |
| 8 | 216900 | 1 | 27 | 22 | 5 | 1.163291685 | 1.380175659 |
| 9 | 173400 | 1 | 171 | 166 | 5 | 7.367514003 | 10.4140527 |
| 10 | 167100 | 1 | 186 | 180 | 6 | 8.013787161 | 11.2923463 |
| 11 | 138900 | 1 | 172 | 160 | 12 | 7.41059888 | 10.03764115 |
| 12 | 104500 | 1 | 40 | 35 | 5 | 1.723395088 | 2.195734003 |
| 13 | 78200 | 2 | 170 | 167 | 3 | 7.324429125 | 10.47678795 |
| 14 | 54700 | 1 | 20 | 15 | 5 | 0.861697544 | 0.941028858 |
| 15 | 33300 | 3 | 154 | 154 | 0 | 6.63507109 | 9.661229611 |
| 16 | 28800 | 1 | 420 | 146 | 274 | 18.09564843 | 9.159347553 |
| 17 | 20500 | 1 | 484 | 195 | 289 | 20.85308057 | 12.23337516 |
Simulation results suggest that FCM-ECSB method is hard to adopt for digestion models having few bands or those show little SFBs. For example Y. pestis (XbaI) and S. fluxneri (SpeI). They showed SFBs by 23.67% and 28.14% respectively. A possible solution might be using a pixel density calibration ladder that show only SFBs or Hunter’s DNA ladder SFBs bands in combination with standardized relative percentage described by Warner and Onderdonk (18) to eliminate variations between different lanes. Furthermore, our simulation results showed DMs of some strains completely representing SFB by 13 expected PFGE bands; namely AscI digestions of L. monocytogenes strains L2626, 2015TE19005-1355 and 2015TE24968 with NCBI accession number CP007684.1, CP014261.1 and CP014790.1 respectively (supplementary material 4 (S4)). These strains can be used as pixel density calibration ladders. But depending on Hunter’s ladder SFB bands more reliable that suggested PD calibration ladders can only be introduced in future PFGE results. Testing this claim in wetlab PFGE is also critical.
Regarding evaluation of PFGE results based on correlation coefficients of both marker band size vs. rF and then band size vs. pixel density; many factors affecting PFGE bands were not considered in our work. Detailed evaluation criteria of PFGE including markers rF vs. BS equation were described by Georing [29]. We will focus on our suggested pixel density normalization method (FCM-ECSB). Initial cell concentration is a determining factor of band intensity profile after Ethedium Bromide staining. It is also critical for our suggested method that PFGE bands are saturated by the dye [9,13].
PFGE images used for meta-analysis to demonstrate FCM-ECSB method were obtained in different resolutions. Consequently, pixel densities obtained are greatly affected by resizing of images during production of cited articles. Qualities of cameras fitted with documentation systems used to obtain images are also significant factors. Not to mention quality of Ethedium bromide staining and conversion of images from colored to negative and then black and white. Since manual modifications were made during lane and PFGE bands assignment, human error also might affected our conclusions. That GelAnalyzer 2010 image analysis software calculates pixel densities according to width of bands which were manually modified in many cases. It is also important to mention that separation of bands in few cases was incomplete; that intersection of successive bands was observed. Correction of such intersection is also important for our FCM-ECSB that is affect pixel densities of both bands. The most critical step in our opinion is the removal of odd PD bands, that EPD equation is sensitive especially when number of bands is few. Conclusions made to evaluate PFGE quality depended only on correlation coefficients of both BS vs. rF and BS vs. PD equations. FCM-ECSB algorithm is obviously sensitive to presence of ghost bands especially those resulted from incomplete digestion. That incomplete digestion affects pixel densities of two bands in addition to presence of a false one.
Last but not least, we did not perform a comparison between multiple FCM-ECSB results. For performing such comparisons, total estimation errors of both PFGE profiles must be taken into account. The relationship between position tolerance and critical co-migration threshold must be clarified. Obviously, position tolerance will stay as an important parameter and possibly profile resolution of each individual PFGE profile (expressed as CCT).
Digestion models derived from WGS
PFGE simulation demonstrated here may provide a powerful tool for studies targeting evaluation of multilaboratory performance and quality control of interlaboratory comparisons across members of PNI. We suggest that running distance is actually a function of CCT, that the longest the run, more close-length fragments separate. Simulation results in supplementary material 4 (S4) shows expected PFGE bands and corresponding FCMs. It may also be possible to mathematically convert percentages of differences (simulation matrix, Figure 1) into simulated rF values to figure out the relationship between adopted position tolerance of rF and our described CCT. That will be necessary to evaluate our database algorithm (GelToWGS) refer to figure 2. Multi-laboratory evaluation now may have predicted PFGE profiles upon which results of each lab can be scored upon. In-complete digestion can be also avoided by optimizing digestion time and enzyme concentration (unit/gel plug) based on predicted PFGE profiles mentioned earlier.
Since plasmid interference show false positive PFGE bands, plasmids were excluded from GelToWGS database and WGSToGel simulations in this work; such interference was reported in PFGE profiles of C. jejuni and C. coli which resulted in false chromosome size estimation [30]. Similar results were reported to limit discriminatory powers of both XbaI and SpeI for typing chromosomes of S. enterica [5]. Such interference can be evaluated if plasmid digestion profiles are associated with each DM. This is the intended upgrade to GelToWGS database. Alongside, PFGE simulation algorithms can also be upgraded.
Some FASTA sequences contained ambiguous nucleotides which may have masked some recognition and/or restriction sites of enzymes used. DNA methylation which reported to result in false negative bands might also affect our simulation and GelToWGS comparison results. We suggest that invention of new bioinformatics tools those takes into account nucleotide ambiguity and DNA methylation within recognition sequences of these enzymes will increase accuracy.
GelToWGS database comparison results of Hunter’s DNA ladder
The main idea was to predict Dice similarities assuming that query fragments were run under the same conditions as wet-lab PFGE isolate under investigation (Hunter’s DNA ladder, supplementary material 4 S4). So that, parameters of wet-lab PFGE are the critical factors those determine whole conclusions returned by GelToWGS database server. In other words” GelToWGS database results are only as good as wet-lab PFGE work”. The main factor is CCT value selection. It is still obscure because it is hard to determine resolution of PFGE. It depends on running distance alongside other electrophoresis conditions [29]. Another important aspect is plasmid contamination that might result in false positive bands. In this case, conclusions made by the current version of the database are skewed. Future upgrades to the system will include plasmid digestion models. Although this upgrade itself may result in more complicated conclusions.
In results section we showed top 1 match with Hunter’s DNA ladder (S. enterica chromosome with accession number CP017617.1), which we concluded that it is not epidemiologically related to Hunter’s ladder. Here we would like to reveal common and rarely matched DNA fragments across the whole tested DMs with each band of the marker. As shown in figure 1, sometimes multiple query fragments may match with a single PFGE band. In such case, FCM will determine number of matches for that given fragment (actual matches). Total query matches comprise 2,321 fragment while actual matches were 1,594 which means that 727(31.23%) fragment were excluded due to co-migration. When considering bands of Hunter’s DNA ladder; query and actual matches show that 10 PFGE bands (12 DNA fragments according to FCM-ECSB) matched with bands #17 to #15, #9 to #11, #7 and #2 comprised 93.84% and 92.41% of all query and actual matches respectively. While the rest of the bands (8 bands representing FCM value of 1 for each) combined have only shown 6.16% and 7.59% of all query and actual matches respectively table 3. Notice that the difference between query and actual matches is a strong evidence that show how ignoring co-migration in PFGE analysis adversely affect epidemiological conclusions. For example; band #17 (20.5 kbp) matched with 289 query fragment across digestion models tested, but when considering the fact that this PFGE band in the marker is a SFB, number of matches drops to 195 (289 match excluded due to co-migration). Alongside, when we consider co-migrated fragments of the ladder; namely bands #13 (2 fragments) and #15 (3 fragments), exclusions due to co-migration dropped to 3 and zero respectively table 3.
These results reveal the most common fragments with the marker across all XbaI digestion models of S. enterica those show at least one match with Hunter’s ladder. (197 out of 420). We argue that degree of matches with each band in the marker reflect evolutionary events and consequently selective pressures those lead to these different pulsotypes. WGS analysis will better consider this issue [31]. Furthermore, DMs those didn’t show any match can be considered as different pulsotypes. Our data clearly show that band #1 is very rare that a single match was shown. While band #17, #16 and #2 are much common table 3. Since PFGE reflects number of recognition sites of the enzyme and their distribution across the chromosome, frequency of common bands across a clonal group reflects how conservative or dynamic the two restriction sits those result in the fragment. GelToWGS database does not store DNA sequence of the fragment or it’s location within the chromosome. It will be informative to do in future upgrades.
PFGE simulation results (WGSToGel algorithms)
The target of our simulation was to generate results those are the same, or at least highly similar to FCM-ECSB image analysis algorithm suggested. The most important question is that does Dice percentage of difference used actually express behavior of DNA fragments during wet-lab PFGE? The answer to this critical question requires wet-lab FCM-ECSB confirmations for bacterial isolates which it’s chromosomal sequences were included in WGSToGel simulation results shown in supplementary material 4 (S4) or similar data. According to such findings, WGSToGel simulations can be modified in terms of how difference is calculated. But its main logic will probably remain unchanged.
Possible future upgrades to currently used computer-assisted analysis of bacterial epidemiology based on findings of this study
FCM-ECSB algorithm can be included in gel image analysis software, automatic detection of co-migrated fragments and ghost bands can also be done. Shifting from using ordinary position tolerance of rF to band size, marker error and FCMs will require larger computer platform. It may also be possible to compare PFGE results to digestion models simply by denotation of fragment sizes into marker equation to calculate rF values. This method will play a significant rule in figuring out the relationship between adopted position tolerance and CCT if PFGE has been performed for the same isolate that have been sequenced and in-silico digested. Since demonstrated algorithms showed ability of storing the same fragment sizes from either PFGE images and WGS, our database is similar to MLVABank database which stores MLVA typing data from both capillary electrophoresis and WGS [32]. Our prototype database may play the rule of linking PulseNet international network database (BioNumerics) and the WGS database dedicated to bacterial genomes GenomeTrakr [31,33].
Conclusion
Proposed approaches may collectively improve our understanding of population dynamics and evolution of pathogenic bacteria in many aspects. Since adoption of PFGE for outbreak investigations in 1996 [12], in the United States alone >800,000 PFGE records are stored in PulseNet USA database. Records are shared within PNI contributing laboratories [33,34]. All these years’ comparisons of PFGE findings were ignoring co-migration of different DNA fragments. Our simulation results suggest that about 35% of PFGE profiles representing co-migrated fragments. This finding partially support our suggestion that “odd values of pixel density across a PFGE profile” represent either ghost bands or co-migrated fragments. This finding is critical for our image analysis algorithm suggested but it still needs further evaluation. Due to absence of a method that reveal number of co-migrated fragments, genetic variations due to co-migration of DNA fragments remained hidden. Findings reported by Warner and Onderdonk support this claim [19]. The described FCM-ECSB image analysis algorithm (if standardized) will provide an important tool to look back and reassess previously made epidemiological conclusions. Based on the same approach, PFGE result might be archived in a database that store band sizes, FCM results and electrophoresis parameters those include correlation coefficients of BS vs. pixel densities and BS vs. rF as numerical data. Such database would not only add a third dimension to PFGE images but it will also require a significantly less storage space. Since our suggested algorithms which resulted in previously mentioned conclusions were based on testing WGSs of all bacterial species those have standard PFGE typing protocols adopted by PNI, in addition to the fact that geltowgs.uofk.edu database is available online, future research targeting evaluation of mentioned algorithms is feasible and necessary.
Since epidemiological surveillance is turning toward whole genome sequencing [18], linking old PFGE data to WGS results by means of simulation demonstrated here (WGSToGel) will provide a chance to take hundreds of thousands of PFGE epidemiological data accumulated during the last 24 years into account [33] while approaching the new WGS era. Such comparisons will only differ from upper and lower limits mentioned earlier in that band sizes are the simulations results, CCT is based on the simulation and Hunter’s DNA ladder error is from wet-lab PFGE results. On the other hand, while turning to WGS process may take some time, new PFGE data could be simultaneously compared to both old PFGE data and new WGS results.
Author Contributions
Study design, NCBI search and downloading FASTA files, mathematical methods (modeling and algorithms), FCM-ECSB image analysis, SQL database and website programming, SQL simulation algorithms, interpretation of results, statistical analysis and initial manuscript writing by I-E A. In-silico digestion and formulation of some mathematical equations by IA. In-silico digestion of whole chromosome sequences was done by the team that included: I-EA, IA, AE, HB, AM, EA, SM, SA, WM, AE, MO and FE.
Conflict of Interests
The described FCM-ECSB method, the methods of mathematical modeling and simulation algorithms, database, web application, logo and the name GelToWGS© were patented to the first and second authors. Accordingly, the use of any one of previously mentioned methods and/or algorithms without permission for upgrading image analysis software or any bioinformatics tool, creating another web or any offline software that apply the methods/algorithms is considered a financial conflict of interests.
Funding Statement
This work was partially funded by scientific research administration (SRA), University of Khartoum, Sudan. SRA supported construction of prototypes of both; SQL GelToWGS database and the website. In addition, they provided server computer and hosting of evaluation copy of the database by the domain name server (DNS) of the same university.
Acknowledgement
The authors are grateful to Dr. Faisal M Fadelmoula; director of the Center for Bioinformatics and System Biology (Faculty of Science, University of Khartoum, Sudan) for providing a computer facility for training data entry on using DNADynamo™ software and some data entry. The authors appreciate the efforts of the team who validated the bioinformatic basis, mathematical modeling method, database algorithms and website construction. The team includes; Prof. Omran F Othman (Department of Zoology, Faculty of Science, University of Khartoum) Dr. Abd-Elhameed A Mansur (Dept. of Computer and information technology, Faculty of Mathematics and computer Science, University of Khartoum), Dr. Muhsin H. Abdalla (Department of applied mathematics, Faculty of Mathematics and computer Science, University of Khartoum), Dr. Ahmed M Elsawe (Africa city of technology, Sudan). We also appreciate the useful discussion with Mr. Mahmood M Abdulhaleem for his valuable advice for GelToWGS SQL database design.
Supplementary Materials
Supplementary material 1 S1 (video file) | Screenrecorded video that demonstrate all calculations of FCMECSB image analysis algorithm. The video shows analysis of PFGE profile of E. coli O157:H7 strain G5244. Web link is here
Supplementary material 2 S2 (Microsoft Excel workbook) | samples size of this study; the workbook shows NCBI GeneBank accession numbers and identification of bacterial species and strains used in this study. (File size 49 KB)
Supplementary material 3 S3 (Microsoft Excel workbook) | Results returned by GelToWGS database that show comparisons of FCM-ECSB results of Hunter’s DNA ladder compared to various XbaI digested chromosome sequences of S. enterica obtained from NCBI GeneBank database (file size: 652 KB).
Supplementary material 4 S4 (Microsoft Excel workbook) | PFGE simulation results obtained using WGSToGel algorithms (file size: 4.37 MB).
Roberts RJ, Vincze T, Posfai J, Macelis D (2003) REBASE : restriction enzymes and methyltransferases. 31: 418-420. [ Ref ]
McClelland M, Jones R, Patel Y, Nelson M (1987) Restriction endonucleases for pulsed field mapping of bacterial genomes. Nucleic Acids Res 15: 5985-6005. [ Ref ]
Stephenson FH (2003) Calculations for Molecular Biology and Biotechnology: A Guide to Mathematics in the Laboratory. [ Ref ]
Singer RS, Sischo WM, Carpenter TE (2004) Exploration of biases that affect the interpretation of restriction fragment patterns produced by pulsed-field gel electrophoresis. J Clin Microbiol 42: 5502-5511. [ Ref ]
Anh T, Le H, Roumagnac P, Grimont PAD, Scavizzi MR (2007) Clonal Expansion and Microevolution of Quinolone-Resistant Salmonella Clonal Expansion and Microevolution of Quinolone-Resistant Salmonella enterica Serotype Typhi in Vietnam from 1996 to 2004. Journal of Clinical Microbiology. [ Ref ]
Argudín MA, Rodicio MR, Guerra B (2010) The emerging methicillinresistant Staphylococcus aureus ST398 clone can easily be typed using the Cfr9I SmaI-neoschizomer. Lett Appl Microbiol 50: 127-130. [ Ref ]
Schwartz DC, Koval M (1989) Conformational dynamics of individual DNA molecules during gel electrophoresis. Nature 338: 520-522. [ Ref ]
Herschleb J, Ananiev G, David SC (2007) Pulsed-field gel electrophoresis. Nat Protoc 2: 677-684. [ Ref ]
Struelens MJ, De Ryck R, Deplano A (2001) Analysis of Microbial Genomic Macrorestriction Patterns by Pulsed-Field Gel Electrophoresis (PFGE) Typing. New Approaches for the Generation and Analysis of Microbial Typing Data. Elsevier Science. [ Ref ]
Belkum AVAN, Leeuwen WVAN, Kaufmann ME, Cookson B, Forey O, et al. (1998) Assessment of Resolution and Intercenter Reproducibility of Results of Genotyping Staphylococcus aureus by Pulsed-Field Gel Electrophoresis of Sma I Macrorestriction Fragments : a Multicenter Study. J Clin Microbiol 36: 1653-1659. [ Ref ]
Goering RV (2010) Pulsed field gel electrophoresis: A review of application and interpretation in the molecular epidemiology of infectious disease. Infect Genet Evol 10: 866-875. [ Ref ]
Hunter SB, Vauterin P, Lambert-fair MA, Duyne MS Van, Kubota K, et al. (2005) Establishment of a Universal Size Standard Strain for Use with the PulseNet Standardized Pulsed-Field Gel Electrophoresis Protocols : Converting the National Databases to the New Size Standard. J Clin Microbiol 43: 1045-1050. [ Ref ]
Gebhart C (2014) Molecular Microbiology: Diagnostic Principles and Practice. Laboratory Medicine. ASM Press, Washington, DC. [ Ref ]
Belkum A Van, Tassios PT, Dijkshoorn L, Haeggman S, Cookson B, et al. (2007) Guidelines for the validation and application of typing methods for use in bacterial epidemiology. Clinical Microbiology and Infection 13:1-46. [ Ref ]
Li A, Chen X, Ugaz VM (2010) Miniaturized System for Rapid Field Inversion Gel Electrophoresis of DNA with Real-Time Whole-Gel Detection. Anal Chem 82: 1831-1837. [ Ref ]
Nameghi SA, Microbiology C (2007) Genotyping Escherichia coli isolates by Pulsed-Field Gel Electrophoresis. Sodertorn University. [ Ref ]
Swaminathan B, Gerner-Smidt P, Ng L-K, Lukinmaa S, Kam K-M, et al. (2006) Building PulseNet International: An Interconnected System of Laboratory Networks to Facilitate Timely Public Health Recognition and Response to Foodborne Disease Outbreaks and Emerging Foodborne Diseases. Foodborne Pathog Dis 3: 36-50. [ Ref ]
Nadon C, Walle I Van, Gerner-smidt P, Campos J, Chinen I, et al. (2017) PulseNet International : Vision for the implementation of whole genome sequencing (WGS) for global food- borne disease surveillance. Euro Surveill 22: 1-12. [ Ref ]
Warner JE, Onderdonk AB (2003) Method for Optimizing Pulsed-Field Gel Electrophoresis Banding Pattern Data. J Mol Diagnostics 5: 21-27. [ Ref ]
Struelens MJ, De Ryck R, Deplano A, Dijkshoorn L, Towner KJ, et al. (2001) New Approaches for the Generation and Analysis of Microbial Typing Data. Analysis of microbial genomicmacro- restriction patterns by pulsed-field gel electrophoresis (PFGE) typing. Elsevier, Amsterdam. [ Ref ]
CDC (2019) PulseNet International: On the path to implementing whole genome sequencing for foodborne disease surveillance. CdcGov. [ Ref ]
Schweitzer N, Dán Á, Kaszanyitzky É, Samu P, Tóth ÁG, et al. (2011) Molecular Epidemiology and Antimicrobial Susceptibility of Campylobacter jejuni and Campylobacter coli Isolates of Poultry, Swine, and Cattle Origin Collected from Slaughterhouses in Hungary. J Food Prot 74: 905-911. [ Ref ]
Kam KM, Luey CKY, Parsons MB, Cooper KLF, Nair GB, et al. (2008) Evaluation and Validation of a PulseNet Standardized Pulsed-Field Gel Electrophoresis Protocol for Subtyping Vibrio parahaemolyticus : an International Multicenter Collaborative Study. J Clin Microbiol 46: 2766- 2773. [ Ref ]
Han H, Zhou H, Li H, Gao Y, Lu Z, et al. (2013) Optimization of Pulse- Field Gel Electrophoresis for Subtyping of Klebsiella pneumoniae. Int J Environ Res Public Health 10: 2720-2731. [ Ref ]
Lazar IL (2010) GelAnalyzer 2010a. [ Ref ]
Hammer O, David ATH, Ryan PD (2001) PAST: Paleontological Statistics Software Package for Education and Data Analysis. Palaeontol Electron 4: 9. [ Ref ]
Tenover FC, Arbeit RD, Goering RV, Mickelsen PA, Murray BE, et al. (1995) Interpreting chromosomal DNA restriction patterns produced by pulsed- field gel electrophoresis: Criteria for bacterial strain typing. J Clin Microbiol 33: 2233-2239. [ Ref ]
Gudmundsdottir S, Hardardottir H, Gunnarsson E (2003) Subtyping of Salmonella enterica Serovar Typhimurium Outbreak Strains Isolated from Humans and Animals in Iceland. J Clin Microbiol 23: 4833-4835. [ Ref ]
Goering RV (2010) Pulsed field gel electrophoresis: A review of application and interpretation in the molecular epidemiology of infectious disease. Infect Genet Evol 10: 866-875. [ Ref ]
Devane ML, Gilpin BJ, Robson B, Klena JD, Savill MG, et al. (2013) Identification of Multiple Subtypes of Campylobacter jejuni in Chicken Meat and the Impact on Source Attribution. Agriculture 3: 579-595. [ Ref ]
Worley J, Meng J, Allard MW, Brown EW, Timme RE (2018) Salmonella enterica phylogeny based on whole-genome sequencing reveals two new clades and novel patterns of horizontally acquired genetic elements. MBio 9: e02303-18. [ Ref ]
MLVABank for microbes Genotyping User Guide – version 1.4.0. (2018) University Paris-Sacla, Paris. [ Ref ]
Tolar B, Joseph LA, Schroeder MN, Stroika S, Ribot EM, et al. (2019) An Overview of PulseNet USA Databases. Foodborne Pathog Dis 16: 457- 462. [ Ref ]
Scallan E, Hoekstra RM, Angulo FJ, Tauxe RV, Widdowson MA, et al. (2011) Foodborne illness acquired in the United States-Major pathogens. Emerg Infect Dis 17: 7-15. [ Ref ]