Journal Name: Journal of Biomedical Research and Reviews
Article Type: Research
Received date: 23-August-2019
Accepted date: 18-September-2019
Published date: 25-September-2019
Citation: Ara I (2019) Modeling the Electrical Activity of Heart. J Biomed Res Rev Vol: 2, Issu: 2 (22-26).
Copyright: © 2019 Ara I. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.p>
Abstract
Mathematical models of electrical activity in cardiac tissue are becoming increasingly powerful tools in the study of cardiac arrhythmias. In this paper a finite-element surface model of human heart is developed, in order to study atrial electrical activation. To characterize electrical activity of atrial and SAN, Fitzhugh-Nagumo equations were employed. Equations were tested using a simplified 3D geometrical model containing both atria and ventricle. The model is able to generate spontaneous activation of electrical impulses. This study represents the first stage toward the development of an accurate computer model of heart activation. The entire system was solved using COMSOL Multiphysics finite-element software. COMSOL Multiphysics is a finite-element software package providing a convenient way for implementing multiphysics models.
Keywords
Mathematical Model, FitzHugh Nagumo Model, Finite Element method, COMSOL.
Abstract
Mathematical models of electrical activity in cardiac tissue are becoming increasingly powerful tools in the study of cardiac arrhythmias. In this paper a finite-element surface model of human heart is developed, in order to study atrial electrical activation. To characterize electrical activity of atrial and SAN, Fitzhugh-Nagumo equations were employed. Equations were tested using a simplified 3D geometrical model containing both atria and ventricle. The model is able to generate spontaneous activation of electrical impulses. This study represents the first stage toward the development of an accurate computer model of heart activation. The entire system was solved using COMSOL Multiphysics finite-element software. COMSOL Multiphysics is a finite-element software package providing a convenient way for implementing multiphysics models.
Keywords
Mathematical Model, FitzHugh Nagumo Model, Finite Element method, COMSOL.
Introduction
Electrical activity is responsible for the periodic contraction and relaxation cycle of the cardiac that propels blood throughout the body. Hence, electrical activity is essential for the cardiac to perform its function [1]. Mathematical modeling of cardiac electrical activity is performed from the cell, tissue and organ levels through to the body surface level [2]. Initiation of the heartbeat occurs in the specialised pacemaker cells of the sinoatrial node (SAN), located in the right atrial wall of the heart. From there, the electrical impulse spreads across the surface of the atria before reaching the ventricles. In this study, preliminary finite-element models of human heart consisting of SAN and atrial region are described.
Methods
One of the simplest single cell models is what is now called the FitzHugh–Nagumo (FHN) model. The model was originally developed as simplification of the Hodgkin–Huxley model by FitzHugh in 1961. The FHN model is simple to implement and computationally inexpensive [3]. In the Atrial region the modified Rogres-McCulloch formulation was used, also suitably scaled:
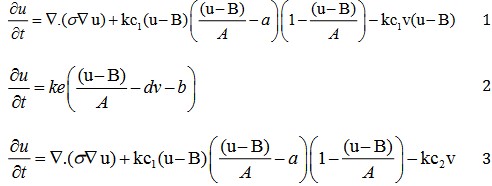
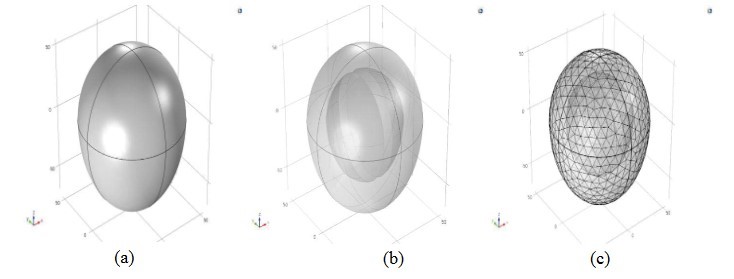
Figure 1: Geometry of heart (a) Solid structure, (b) Semitransparent View, and (c) Mesh geometry.
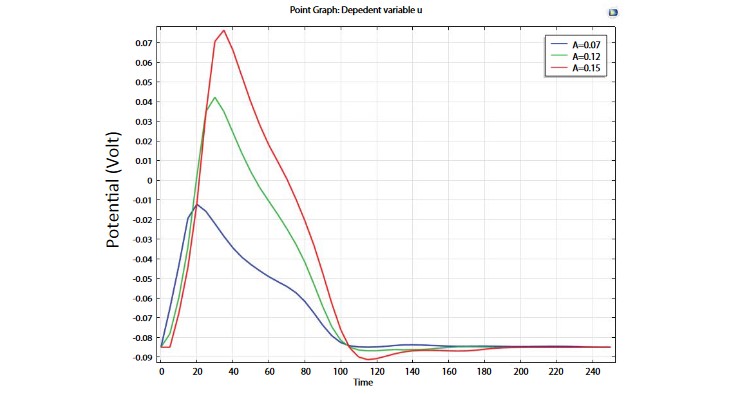
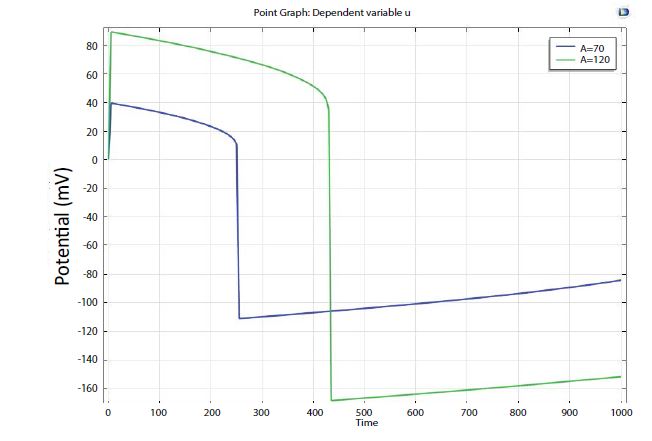
Figure 2:Influence of model parameter ‘A’ on action potential amplitude of Atrial.
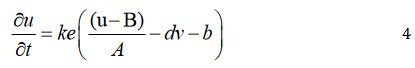
Where, u denotes the membrane potential and v governs cellular refractoriness; v denotes the tissue conductance, nominally set to a value of 0.001 S/m. Remaining parameters are given in Table 1. Initial conditions for (1)-(4) are given in Table 2 [4,5].
Results and Discussion
In order to solve the cellular excitation equations, the model was tested using a highly simplified geometry shown in Figure 1. The entire system of PDEs (1) - (4) was solved using COMSOL Multiphysics finite-element software.
Parameter values which used for simulation are listed in Table 1. COMSOL took approximately 10 minutes to solve 1 simulated second with 1 ms resolution of the potential. Spontaneous activation occurred in the SAN and then spread throughout the atria. Parameters sensitivities are shown on Figure 2 to Figure 7, where times are in second and amplitudes are in volt.
Figure 2 and illustrate results of sweeping action potential amplitude in the atrial by varying parameter A from Table 1 in three steps within the range from 0.07 to 0.15. The results indicate that action potential amplitude increases if the values of parameter ‘A’ increase.
Table 1: Parameters value of modified FitzHugh-Nagumo model [5,7].
| Parameter | Atrial Value | SAN Value |
|---|---|---|
| a | 0.13 | -1 |
| b | 0 mV | -0.29 mV |
| c1 | 0.26 | 1.9 |
| c2 | 0.1 mV | 1mV |
| d | 1 | 0 |
| e | 0.013 | 0.06 |
| A | 140 mV | 35 mV |
| B | -85 mV | -30mV |
| k | 3 ms-1 | 3 ms-1 |
| σ | 0.001 S/m | 0.001 S/m |
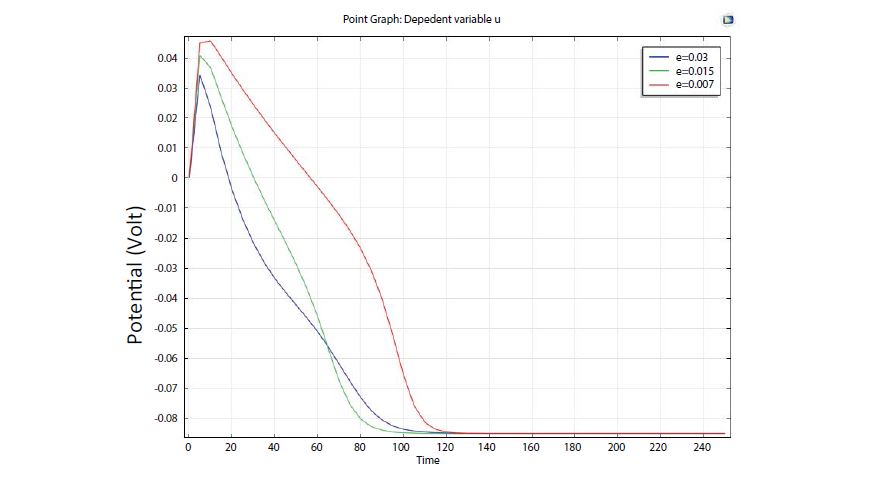
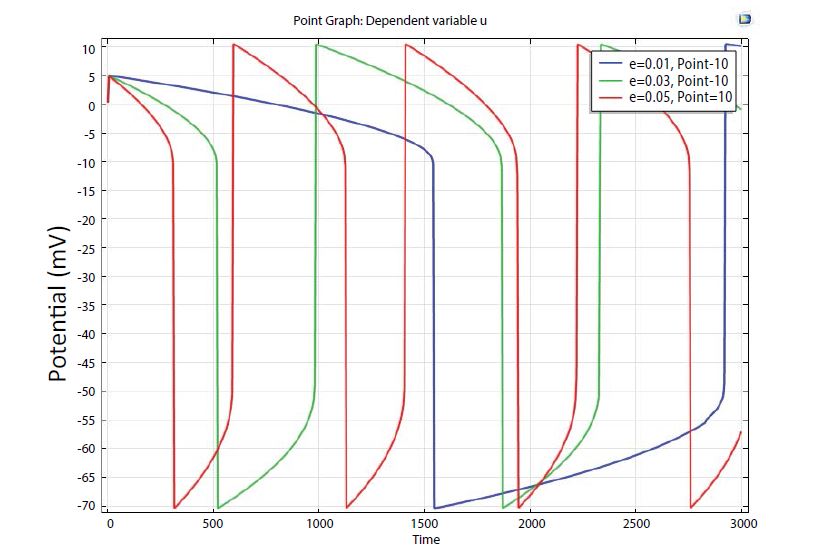
Figure 3: Influence of model parameter ‘e’ on action potential duration of Atrial.
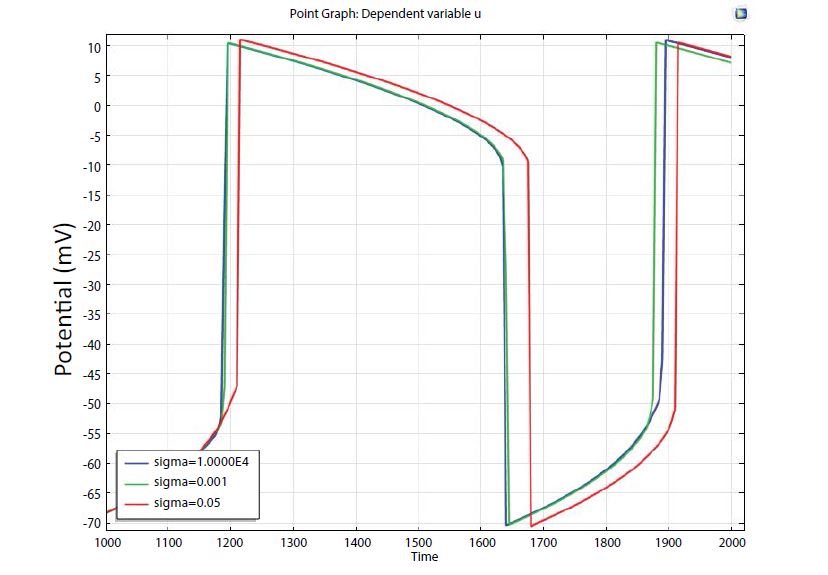
Figure 4: Influence of model parameter ‘σ’ on conduction velocity of Atrial.
Figure 5: Influence of model parameter ‘A’ on action potential amplitude of SAN.
Figure 6: Influence of model parameter ‘e’ on action potential duration of SAN.
Figure 7: Influence of model parameter ‘σ’ on conduction velocity of SAN.
Table 2: Model initial values [5].
| Parameters | Atrial values | SAN values |
|---|---|---|
| u[V] | -0.085 | -0.06 |
| v | 0 | 0 |
The simulated result of Figure 3 and Figure 6 indicates that action potential duration sweep linearly by varying parameter ‘e’ in the atrial and SAN region. Three steps sweeping of ‘e’ are shown in this present study. The results indicate that action potential duration increases by decreasing value of ‘e’.
Figure 4 illustrates the effect of varying atrial conductivity ‘σ’, on the action potential. The conductivity is directly related to the conduction velocity. Lowering the conductivity in the atrial produced delayed action potential.
Figure 5 illustrates results of sweeping action potential amplitude in the SAN by varying parameter ‘A’ from table 1.
Figure 7 illustrates the effect of varying SAN conductivity ‘σ’, on the action potential.
The results of this study indicate that the simplified 3D FHN model of heart can generate action potential. In this paper sensitivity of model parameters on action potential are presented. This model can be used as a tool in basic research and in ECG generation.
Conclusion
Present approach has several limitations: the AV node, Purkinj fiber and also Bundle of his were not considered here. A sensitivity analysis has shown that the most critical parameters of the FitzHugh Nagumo model are e, A, and σ. Numerical simulations on a three dimensional domain was simulated to show the behavior.
Pullan AJ, Buist ML, Cheng LK (2005) Mathematically modeling the electrical activity of the heart: From Cell to Body Surface and Back Again, Singapore, World Scientific Publishing Co. [ Ref ]
Jacquemet V, van Oosterom A, Vesin J-M, Kappenberger L (2006) Analysis of electrocardiograms during atrial fibrillation. Engineering in Medicine and Biology, 25: 79-88. [ Ref ]
R FitzHugh (1961) Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys J 1: 445-466. [ Ref ]
JM Rogers, AD McCulloch (1994) A collocation-Galerkin finite element model of cardiac action potential propagation. IEEE Transactions on Biomedical Engineering 41: 743- 757. [ Ref ]
Dokos S1, Cloherty SL, Lovell NH (2007) Computational Model of Atrial Electrical Activation and Propagation, Conf Proc IEEE Eng Med Biol Soc 2007: 908-911. [ Ref ]
Dokos S (2016) Modeling Organs, Tissues, cells and Devices using MATLAB and COMSOL Multiphysics, Springer Publication. [ Ref ]
Filippi S, Cherubini C. Electrical signals in a heart, Application ID: 981, University campus Biomedico Di Roma, Italy. [ Ref ]