A new framework in quantum chemistry has been proposed recently (“An approach to first principles electronic structure calculation by symbolic-numeric computation” by A. Kikuchi). It is based on the modern technique of computational algebraic geometry, viz. the symbolic computation of polynomial systems. Although this framework belongs to molecular orbital theory, it fully adopts the symbolic method. The analytic integrals in the secular equations are approximated by the polynomials. The indeterminate variables of polynomials represent the wave-functions and other parameters for the optimization, such as atomic positions and contraction coefficients of atomic orbitals. Then the symbolic computation digests and decomposes the polynomials into a tame form of the set of equations, to which numerical computations are easily applied. The key technique is Gröbner basis theory, by which one can investigate the electronic structure by unraveling the entangled relations of the involved variables. In this article, at first, we demonstrate the featured result of this new theory. Next, we expound the mathematical basics concerning computational algebraic geometry, which are necessitated in our study. We will see how highly abstract ideas of polynomial algebra would be applied to the solution of the definite problems in quantum mechanics. We solve simple problems in “quantum chemistry in algebraic variety” by means of algebraic approach. Finally, we review several topics related to polynomial computation, whereby we shall have an outlook for the future direction of the research.

Quantum mechanics, Algebraic geometry, Commutative algebra, Grönber basis, Primary ideal decomposition, Eigenvalue problem in quantum mechanics, Molecular orbital theory; Quantum chemistry, Quantum chemistry in algebraic variety, First principles electronic structure calculation, Symbolic computation, symbolic-numeric solving, Hartree-Fock theory, Taylor series, Polynomial approximation, Algebraic molecular orbital theory.

Dear Readers,

If you are researchers or students with the expertise of physics or chemistry, you might have heard of “algebraic geometry” or “commutative algebra”. Maybe you might have heard only of these words, and you might not have definite ideas about them, because these topics are taught in the department of mathematics, not in those of physics and chemistry. You might have heard of advanced regions of theoretical physics, such as super-string theory, matrix model, etc., where the researchers are seeking the secret of the universe by means of esoteric theories of mathematics with the motto algebraic geometry and quantum mechanics. And you might be desperate in imagining the required endurance to arrive at the foremost front of the study... However, algebraic geometry is originated from rather a primitive region of mathematics. In fact, it is an extension of analytic geometry which you must have learned in highschools. According to Encyclopedia Britannica, the definition of the word goes as follows:

algebraic geometry, study of the geometric properties of solutions of polynomial equations, including solutions in three dimensions beyond three...

It simply asserts that algebraic geometry is the study of polynomial systems. And polynomial is ubiquitous in every branch of physics. If you attend the lecture of elementary quantum mechanics, or you study quantum chemistry, you always encounter secular equations in order to compute the energy spectrum. Such equations are actually given by the polynomial systems, although you solve them through linear algebra. Indeed, linear algebra is so powerful that you have almost forgotten that you are laboring with polynomial algebraic equations.

Be courageous! Let us have a small tour in the sea of QUANTUM MECHANICS with the chart of ALGEBRAIC GEOMETRY. Your voyage shall never be in stormy and misty mare incognitum. Having chartered a cruise ship, the “COMMUTATIVE ALGEBRA”, we sail from a celebrated seaport named “MOLECULAR ORBITAL THEORY”.

The molecular orbital theory [1] in the electronic structure computation of quantum chemistry is computed by the solution of the secular equation, if one adopts the localized atomic orbital basis ${ϕ_{i}}$ defined on the set of atoms at the positions ${R_{i}}$ with other optimizable variables ${ζ_{i}}$ :

$H ({R_{i}}, {ζ_{j}}) \cdot Ψ = E S ({R_{i}}, {ζ_{j}}) \cdot Ψ,$

in which the matrix elements are defined by

$H_{i j} = \int^{} d r ϕ_{i} ℋ ϕ_{j},$

and

$S_{i j} = \int^{} d r ϕ_{i} ϕ_{j} .$

In these expressions, $ℋ$ is the Hamiltonian; the vector $Ψ$ represents the coefficients in LCAO wave-function $Ψ = \sum^{} χ_{i} ϕ_{i}$ ; E is the energy spectrum. The Fock matrix H and the overlap matrix S are, in theory, computed symbolically and represented by the analytic formulas with respect to the atomic coordinates and other parameters included in the Gaussian- or Slater- type localized atomic basis; they are, in practice, given numerically and the equation is solved by means of linear algebra. In contrast to this practice, it is demonstrated by Kikuchi [2] that there is a possibility of symbolic-numeric computation of molecular orbital theory, which can go without linear algebra: the secular equation is given by the analytic form and approximated by the polynomial system, which is processed by the computational algebraic geometry. The symbolic computation reconstructs and decomposes the polynomial equations into a more tractable and simpler form, by which the numerical solution of the polynomial equation is applied for the purpose of obtaining the quantum eigenstates. The key technique is the Gröbner basis theory and triangulation of polynomial set. Let us review the exemplary computation of hydrogen molecule in [2].

Let $ϕ_{i}$ , $Z_{a}$ , $R_{a}$ be the wavefunctions, the atomic charges, and the atomic positions. The total energy functional of Hartree-Fock theory is given by

$Ω = \sum_{i} \int d r ϕ_{i} (r) (- {\frac{Δ}{2}}^{2} + \sum_{a} \frac{Z_{a}}{| r - R_{a} |}) ϕ_{i} (r)$

$+ \frac{1}{2} {\sum_{i, j} \int d r d r}^{'} \frac{ϕ_{i} (r) ϕ_{i} (r) ϕ_{j} (r^{'}) ϕ_{j} (r^{'})}{| r - r^{'} |}$

$- \frac{1}{2} {\sum_{i, j} \int d r d r}^{'} \frac{ϕ_{i} (r) ϕ_{j} (r) ϕ_{j} (r^{'}) ϕ_{i} (r^{'})}{| r - r^{'} |}$

$+ \sum_{a, b} \frac{Z_{a} Z_{b}}{| R_{a} - R_{b} |}$

$- \sum_{i, j} λ_{i, j} (\int d r ϕ_{i} (r) ϕ_{j} (r) - δ_{i, j})$

The secular equation is derived from the stationary condition with respect to the wave-function

$\frac{δ Ω}{δ ϕ_{i}} = 0.$

The energy minimum with respect to the atomic coordinate gives the stable structure:

$\frac{δ Ω}{δ R_{j}} = 0.$

Let us consider the simple hydrogen, as in Figure 1.

Assume that the two hydrogen atoms are placed at $R_{A}$ and $R_{B}$ . By the simplest model, we can choose the trial wave-functions for up- and down- spin at the point $z \in ℝ^{3}$ as follows:

$ϕ_{up} (z) = \frac{1}{\sqrt{π}} (a exp (- z_{A}) + b exp (- z_{B}))$

$ϕ_{down} (z) = \frac{1}{\sqrt{π}} (c exp (- z_{A}) + d exp (- z_{B}))$

Where

$z_{A / B} = | z - R_{A / B} |$

and $a, b, c, d$ are the real variables to be determined. Let ev and ew to be Lagrange multipliers $λ_{i j}$ for $ϕ_{up}$ and $ϕ_{down}$ . Since these two wave-functions are orthogonal in nature, due to the difference of spin, we assume that the multipliers are diagonal: $λ_{i j} = 0$ for $i \neq j$ .

From these expressions, all of the integrals involved in the energy functional are analytically computed. (As for the analytic forms of the integrals, see the supplement of [2].) Then, with respect to inter-atomic distance $R_{A B}$ , Taylor expansion of the energy functional is computed up to degree four, at the center of $R_{A B} = 7 / 5$ . The polynomial approximation is given by

OMEGA = (3571 - 1580*a^2 - 3075*a*b - 1580*b^2 - 1580*c^2 + 625*a^2*c^2 + 1243*a*b*c^2 + 620*b^2*c^2 - 3075*c*d + 1243*a^2*c*d + 2506*a*b*c*d + 1243*b^2*c*d - 1580*d^2

.......................................................................................................... .......................................................................................................... ..........................................................................................................

- 86*a*b*c*d*r^4 - 17*b^2*c*d*r^4 + 12*d^2*r^4 - 4*a^2*d^2*r^4 - 17*a*b*d^2*r^4 + 13*a*b*ev*r^4 + 13*c*d*ew*r^4)/1000

where the inter-atomic distance $R_{A B}$ is represented by r (for the convenience of polynomial processing).

The equations used in the study are quite lengthy, so we only show the part of them. We give the exact ones in the appendix (supplementary material): the energy functional in Appendix A; the secular equations in Appendix B; the Gröbner bases in Appendix C; the triangulation in Appendix D.

In order to reduce the computational cost, the numerical coefficients are represented by the fraction, by the truncation of decimal numbers. We make the change of variables from $a, b, c, d$ to $s, t, u, v$ in the following way:

$a = t + s, b = t - s, c = u + v, d = u - v$

Consequently, the wave-functions are represented by the sum of symmetric and anti-symmetric parts:

$ϕ_{up} (z) = \frac{t}{\sqrt{π}} (exp (- z_{A}) + exp (- z_{B})) + \frac{s}{\sqrt{π}} (exp (- z_{A}) - exp (- z_{B}))$

$ϕ_{down} (z) = \frac{u}{\sqrt{π}} (exp (- z_{A}) + exp (- z_{B})) + \frac{v}{\sqrt{π}} (exp (- z_{A}) - exp (- z_{B}))$

The stationary conditions $\frac{δ Ω}{δ a}$ , $\frac{δ Ω}{δ b}$ , $\frac{δ Ω}{δ c}$ , $\frac{δ Ω}{δ d}$ , with respect to t, s, u, v, yields those equations:

S[1]32*s*u*v*r^4-336*s*u*v*r^3+992*s*u*v*r^2-160*s*u*v*r

.......................................................

+126*t*r^4-882*t*r^3+1748*t*r^2+1896*t*r-12470*t=0

S[2]156*s*u^2*r^4-1068*s*u^2*r^3+2248*s*u^2*r^2-80*s*u^2*r

.......................................................

+992*t*u*v*r^2-160*t*u*v*r+40*t*u*v=0

S[3]156*s^2*u*r^4-1068*s^2*u*r^3+2248*s^2*u*r^2-80*s^2*u*r

.......................................................

+126*u*r^4-882*u*r^3+1748*u*r^2+1896*u*r-12470*u=0

S[4]-52*s^2*v*r^4+236*s^2*v*r^3-32*s^2*v*r^2-104*s^2*v*r

.......................................................

-30*v*r^4+330*v*r^3-1148*v*r^2+760*v*r-170*v=0

The stationary conditions $\frac{δ Ω}{δ e v}$ , $\frac{δ Ω}{δ e w}$ , with respect to ev, ew, are the normalization condition for the wave-functions. They yield two equations:

S[5]-13*s^2*r^4+139*s^2*r^3-458*s^2*r^2+63*s^2*r

.......................................................

-63*t^2*r-3986*t^2+1000=0

S[6]13*u^2*r^4-139*u^2*r^3+458*u^2*r^2-63*u^2*r

.......................................................

+63*v^2*r-14*v^2+1000=0

The stable condition for the molecular geometry δΩ/δr yields this:

312*s^2*u^2*r^3-1602*s^2*u^2*r^2+2248*s^2*u^2*r

.......................................................

+380*v^2+740*r^3-3903*r^2+7288*r-5102=0

For simplicity, however, we replace the last equation with a simple one (of the fixed inter-atomic distance) as follows:

S[7] 5*r-7=0.

It fixes the inter-atomic distance at 1.4.

By processing polynomials S[1],...,S[7], We obtain 18 polynomials in the Grönber basis J[1],...,J[18]. We only show the skeletons of them, because the coefficients are too lengthy. The exact form is given in the appendix.

J[1]=r-1.4
J[2]=(...)*ew^6+(...)*ew^5+(...)*ew^4
+(...)*ew^3+(...)*ew^2+(...)*ew+(...)
J[3]=(...)*ev+(...)*ew^5+(...)*ew^4+(...)*ew^3
-(...)*ew^2-(...)*ew+(...)
J[4]=(...)*v*ew^4+(...)*v*ew^3+(...)*v*ew^2
-(...)*v*ew-(...)*v
J[5]=(...)*v^2-(...)*ew^5-(...)*ew^4-(...)*ew^3
-(...)*ew^2+(...)*ew-(...)
J[6]=(...)*u*ew^4+(...)*u*ew^3+(...)*u*ew^2
+(...)*u*ew+(...)*u
J[7]=(...)*u*v*ew^2+(...)*u*v*ew+(...)*u*v
J[8]=(...)*u^2+(...)*ew^5+(...)*ew^4+(...)*ew^3
+(...)*ew^2-(...)*ew-(...)
J[9]=(...)*t*ew^4+(...)*t*ew^3+(...)*t*ew^2
+(...)*t*ew+(...)*t
J[10]=(...)*t*v*ew^3+(...)*t*v*ew^2+(...)*t*v*ew+(...)*t*v
J[11]=(...)*t*u*ew^3+(...)*t*u*ew^2+(...)*t*u*ew+(...)*t*u
J[12]=(...)*t^2-(...)*ew^5-(...)*ew^4-(...)*ew^3
+(...)*ew^2+(...)*ew-(...)
J[13]=(...)*s*ew^2+(...)*s*ew-(...)*s-(...)*t*u*v*ew-(...)*t*u*v
J[14]=(...)*s*v*ew-(...)*s*v-t*u*ew^2-(...)*t*u*ew-(...)*t*u
J[15]=(...)*s*u*ew+(...)*s*u+(...)*t*v*ew^2+(...)*t*v*ew+(...)*t*v
J[16]=(...)*s*u*v+(...)*t*ew^3+(...)*t*ew^2+(...)*t*ew+(...)*t
J[17]=(...)*s*t-(...)*u*v*ew-(...)*u*v
J[18]=(...)*s^2+(...)*ew^5+(...)*ew^4+(...)*ew^3
-(...)*ew^2-(...)*ew-(...)

The triangular decomposition to the Gröbner basis is computed, which contains five decomposed sets of equations T[1],..., T[5]. Here the only the skeleton is presented, while the details are given in the appendix. Observe that one decomposed set includes seven entries; from the first entry to the last, the seven variables are added one by one, with the order of r, ew, ev, v, u, t, s, in the arrangement of a triangle. Now we can solve the equation by determining the unknown variables one by one. As a result, the triangular decomposition yields four subsets of the solutions of equations: the possible electronic configurations are exhausted, as is shown in Table 1.

T[1]:

_[1]=r-1.4
_[2]=(...)*ew+(...)
_[3]=(...)*ev+(...)
_[4]=v
_[5]=(...)*u^2-(...)
_[6]=t
_[7]=(...)*s^2-(...)

T[2]:

_[1]=r-1.4
_[2]=ew-(...)
_[3]=ev-(...)
_[4]=v^2-(...)
_[5]=u
_[6]=t
_[7]=(...)*s^2-(...)

T[3]:

_[1]=r-1.4
_[2]=ew^2+(...)*ew+(...)
_[3]=ev-ew
_[4]=v^2-(...)*ew-(...)
_[5]=u^2+(...)*ew+(...)
_[6]=t^2+(...)*ew+(...)
_[7]=s+(...)*t*u*v*ew+(...)*t*u*v

T[4]:

_[1]=r-1.4
_[2]=ew+(...)
_[3]=ev+(...)
_[4]=v
_[5]=u^2-(...)
_[6]=t^2-(...)
_[7]=s

T[5]:

_[1]=r-1.4
_[2]=ew+(...)
_[3]=ev+(...)
_[4]=v^2-(...)
_[5]=u
_[6]=t^2-(...)
_[7]=s

This is one of the featured results in [2]. The author of that work had demonstrated the procedure of the computation in a factual way, but he had not explained the underlying mathematical theory so minutely. Consequently, it is beneficial for us to grasp some prerequisites of commutative algebra and algebraic geometry because these theories are still strange to a greater part of physicists and chemists. In the following sections, we review concepts of commutative algebra and algebraic geometry, which are utilized in this sort of computation. Next, we learn about Grönbner bases. We will find that the “primary ideal decomposition” in commutative algebra surrogate the eigenvalue problem of linear algebra. Then we apply our knowledge to solve simple problems of molecular orbital theory from the standpoint of polynomial algebra. In the end, we take a look at the related topics which shall enrich the molecular orbital theory with a taste of polynomial algebra, such as “polynomial optimization” and “quantifier elimination”. The employment of these methods will show the course of future studies.

Our handy tool is polynomial and our chief concern is how to solve the set of polynomial equations. Such topics are the themes of commutative algebra. If we would like to do with geometrical view, the task lies also in algebraic geometry. From this reason, in this section, we shall review mathematical definitions and examples related to the theory of polynomials.

N. B.: The readers should keep in mind that the chosen topics are mere “thumbnails” to the concepts of profound mathematics. As for proofs, the readers should study from more rigorous sources; for instance, for commutative algebra, the book by Eisenbud [3] or the Book by Reid [4]; for algebraic geometry, the book by Perrin [5], for Gröbner bases, the works by Cox, Little, and O’Shea [6,7], the book by Becker and Weispfenning [8], or the book by Ene and and Herzog [9].

A polynomial should be defined in a ring. A ring is composed by the coefficient (in some field) and the indeterminate variables. Let K be the coefficient field. The polynomial ring $S = K [x_{1}, x_{2}, ..., x_{n}]$ is the K-vector space, with the basis elements (monomials) of the form

We define the degree of a monomial $X^{C} = x_{1}^{c_{1}} x_{2}^{c_{2}} .... x_{n}^{c_{n}}$ by

$| X^{C} | = \sum_{i = 1}^{n} c_{i}$

The degree of polynomial is given by

$\deg (f) = \max {| X^{C} | : X^{c} \in supp (f)}$

A homogeneous polynomial is a polynomial, in which every non-zero monomial has the same degree.

$x^{3} + x^{2} y^{} + x^{} y^{2} + y^{3}$ is a homogeneous polynomial of degree 3.
$x^{3} + x^{2} y + z^{2}$ is not homogeneous.

(Homogenization) A non-homogeneous polynomial $P (x_{1}, ..., x_{n})$ is homogenized by means of an additional variable $x_{0}$ .

For $P (x, y, z) = x^{3} + x^{2} y + z^{2}$

$^{h} P (t, x, y, z) = t^{3} ({(\frac{x}{t})}^{3} + {(\frac{y}{t})}^{2} (\frac{y}{t}) + {(\frac{z}{t})}^{2}) = x^{3} + x^{2} y + z^{2} t$

Definition 4.1 An ideal in the polynomial ring is the set of polynomials, which is closed under these operation:

$i_{1} \in I$ and $i_{2} \in I$ then $i_{1} + i_{2} \in I$
$i_{1} \in I$ and $α \in S$ then $α \cdot i \in I$ .

We usually denote an ideal by the generators, such as $I = (x, y)$ or $J = (x^{2} + y^{2}, x y)$ .

The sum and the product of the ideals are defined by

$I + J = {f + g : f \in I and g \in J}$

$I J = {f . g : f \in I and g \in J}$

The ideal quotient is defined to be the ideal

$I : J = {f \in S : f . g \in I for all g \in J}$

For two ideals I and m, the saturation is defined by

$I : m^{\infty} = \cup_{i = 1}^{\infty} I : m^{i}$

(Observe that $I : m^{i} \subset I : m$ for I < j. In many cases, we do not have to consider the union of infinite number of ideal quotients, as the extension by union with $I : m^{i}$ shall “saturates” and stop to grow at some finite i, if the ring is Noetherian, as will be discussed later.)

The radical of an ideal I is defined by

$\sqrt{I} = {f \in S : f^{k} \in I for some integer k > 0}$

Definition 4.2. Let S be the subset of a ring $k [x_{1}, ..., x_{n}]$ . We denote the common zeros of polynomials $P (x_{1}, ..., x_{n})$ in S by

$V (S) = {x \in k^{n} | \forall P (x_{1}, ...., x_{n}) \in S such that P (x) = 0}$

We call $V (S)$ the affine algebraic set (or affine variety) defined by $S$

Example 4.3 In $ℂ [X, Y]$ , $V (X^{2} + Y^{2}) = {X = \pm \sqrt{- 1} Y}$ .
Example 4.4 In $ℝ [X, Y]$ , $V (X^{2} + Y^{2}) = X = Y = 0.$
Example 4.5 In $k [x_{1}, x_{2}, ..., x_{n}]$ , $V ({1}) = \emptyset$ .
Example 4.6 In $k [x_{1}, x_{2}, ..., x_{n}]$ , $V ({0}) = k^{n}$ .

Also, these properties of the affine algebraic set are notable.

If $A \subset B$ , $V (B) \subset V (A)$ .
A point $a = (a_{1}, ..., a_{n})$ is an affine algebraic set: $V (a) = (x - a_{1}, ..., x - a_{n})$
If then $I = (f_{1}, f_{2}, ..., f_{n})$

$V (I) = V (f_{1}) \cap ... \cap V (f_{n})$

The intersection of affine algebraic sets is also an affine algebraic set:

$\underset{J}{\cap} V (S_{j}) = V (\underset{i}{\cap} S_{j})$

Or

$V (I) \cap V (J) = V (I \cap J)$

The finite union of affine algebraic sets is also an affine algebraic set:

$V (I) \cup V (J) = V (I J) = V (I \cap J)$

The interpretation of the saturation $I : J^{\infty}$ in algebraic geometry is this: the saturation is the closure (in the sense of topology) of the complement of $V (J)$ in $V (I)$ .

Definition 4.3 Let be a subset of $k^{n}$ (where k is an arbitrary field). The ideal of $V$ is defined as $I (V) = {f \in k [x_{1}, ..., x_{n}] ∣ \forall x \in V, f (x) = 0}$

In other words, $I (V)$ is the set of polynomial functions which vanish on $V$ .

Example 4.7 $I (\emptyset) = k [X_{1}, ..., X_{n}]$ .

Example 4.8 For the ideal

$I = ((x^{2} - y^{3}) x^{2}),$

the saturation is given by

$I : {(x)}^{\infty} = (x^{2} - y^{3})$

$V (I)$ is the composure of the curve $x^{2} = y^{3}$ and the doubled line $x = 0$ . The saturation $I : {(x)}^{\infty}$ removes the line $x = 0$ from that composure; the point $(x, y) = (0, 0)$ (which lies on $x = 0$ ), however, is not removed, because the saturation is the closure.

The ideal of an affine algebraic set of a ideal I, denoted by $I (V (J))$ , is computable.

Example 4.9 For $J = (Y^{2}, Y^{2}) \subset ℝ [X, Y]$ , $V (J) = {(0, 0)}$ and $I (V (J)) = (X, Y)$ . Observe that the $I (V (J)) \neq J$ . This is the consequence of the famous theorem of Hilbert (Nullstellensatz), which we will learn later.

We can define “residue class rings”. Let $I \subset R$ be an ideal in a ring R, and f is an element in R. The set $f + I = {f + h : h \in I}$ is “the residue class of f modulo I”; f is a representative of the residue class $f + I$ . We denote the set of residue classes modulo I by $R / I$ . It also has the ring structure through addition and multiplication. Several resources use the term “quotient ring” or “factor ring” for the same mathematical object. In general, an ideal depicts geometric objects, which might be discrete points or might be connected and lie in several dimensions. They are represented by the residue class ring:

$k [x_{1}, x_{2}, ..., x_{n}] / I$

Let us see several examples.

Example 4.10 $ℚ [x] / (x^{2} - 2)$ The elements in the ring $R [x]$ are the polynomial $f (x) = a_{0} + a_{1} x + \dots a_{n} x^{n}$ . We divide by , so that

We divide $f (x)$ by $x^{2} - 2$ , so that

$f (x) = b_{0} + b_{1} x + g (x) \cdot (x^{2} - 2)$

The residue $b_{0} + b_{1} x$ is the representative of $f (x)$ when it is mapped into the residue class ring. We might assume that $\bar{x}$ (the representative of $x$ in the residue class ring) would not be an undetermined variable, but a certain number $α$ (outside of $ℚ$ ) such that $α^{2} = 2$ .

Example 4.11 $ℝ [x, y] / (x^{2} + y^{2} - 1)$ .

We assume that the representatives $\bar{x}$ and $\bar{y}$ of $x$ and $y$ in the residue class ring would not be undetermined variables, but a pair of numbers $α$ and $β$ such that $α^{2} + β^{2} = 1$ , and that $(\bar{x}, \bar{y})$ depicts a unit circle, as a one-dimensional geometric object in $ℝ^{2}$ .

Example 4.12

$ℝ [x, y] / (x^{2} + y^{2} - 1, x - y)$

The representative $\bar{x}$ and $\bar{y}$ of $x$ and $y$ are considered to the points or $(1 / \sqrt{2}, 1 / \sqrt{2})$ (which lie in the intersection of $x^{2} + y^{2} = 1$ and $x = y$ ). This example is a simplest case of zero-dimensional ideal.

There are two fundamental types of ideal: prime ideal and primary ideal.

Definition 4.4 An ideal I ( $\subset R$ ) is prime, if $I \neq R$ , and, if $x y \in I$ , then $x \in I$ or $y \in I$ .

Definition 4.5 An ideal I is primary, if $I \neq R$ , and, if $x y \in I$ , then $x \in I$ or $y^{n} \in I$ for some $n > 0$ ; that is to say, every zero divisor of $R / I$ is nil-potent.

Example 2.13 $(x) \subset ℝ [x]$ is a prime ideal.

Example 4.14 P= $(x^{2}, x y, y^{2}) \subset ℝ [x, y]$ is a primary ideal: $x$ and are zero $y$ divisors in $R / P$ ; $x^{2} \in P$ and $y^{2} \in p$ .

Example 4.15 Every prime ideal $p$ is primary.

In the affine algebraic set, these two properties are equivalent.

Ideal $I$ is a prime ideal.
$V (I)$ is irreducible.

In order to unify the algebraic and geometric views, let us review the correspondence between varieties and ideals. There are correspondences:

${Ideals of k [x_{1}, \dots, x_{n}]} \underset{\to}{V} {Subsets X of k^{n}}$

and

${Subsets X of k^{n}} \underset{\to}{I} {Ideals of k [x_{1}, \dots, x_{n}]}$

Where the ideal $I (X)$ and the variety $V (J)$ are defined in the previous sections.

Also there are one-to-one correspondences:

$\begin{matrix} {Radical ideals of k [x_{1}, ..., x_{n}]} & \leftrightarrow & {Varieties X \subset k^{n}} \\ \cup^{} & \cup^{} \\ {Prime ideals of k [x_{1}, ..., x_{n}]} & \leftrightarrow & {Irreducible varieties X \subset k^{n}} . \end{matrix}$

Example 4.16 For the ideal $I = (x^{2}) \subset ℝ [x]$ , $\sqrt{J} = (x)$ . We have $V (I) = V (\sqrt{I})$ .

Example 4.17 For the non-prime ideal $I = (x y) \subset ℝ [x]$ , $V (I) = V (x) \cup V (y)$ .

When we compute or analyze $V (I)$ for an ideal $I$ , it might be convenient for us to work with $V (\sqrt{I})$ or its irreducible component $V (p_{i})$ because the defining ideal would be simpler. The principle of “divide and conquer” is equally effective in symbolic computation.

Definition 4.6 A ring is Noetherian when it is finitely generated.

This means that there is no infinite ascending sequence of ideals: if there is an ascending sequence of ideals, such that

$I_{1} \subseteq ... \subseteq I_{k - 1} \subseteq I_{k} \subseteq I_{k + 1} \subseteq ...$

it terminates somewhere in the following sense:

$I_{n} = I_{n + 1} = \dots$

Example 4.18 $ℝ [x_{1}, x_{2}, ..., x_{n}]$ and $ℂ [x_{1}, x_{2}, ..., x_{n}]$ are Noeterian rings. If there is a computational process in these rings which would create the ascending sequence of ideals, it must terminate after finite number of steps.

Example 4.19 If R is a Noetherian ring, then $R [X]$ is Noetherian (as the consequence of the Hilbert basis theorem) [3]. By induction, is also a Noetherian ring.

Example 4.20 The power series ring $R [[x]]$ is a Noetherian ring.

Example 4.21 If R is a Noetherian ring and I is a two-sided ideal (such that for $a \in R$ , $a I \subset I$ and $I a \subset I$ ), then the residue class ring is $R / I$ also Noetherian. In other words, the image of a surjective ring homomorphism of a Noetherian ring is Noetherian.

Let X be a topological space. The dimension of X is the maximum of the lengths of the chains of irreducible closed subsets of X. The chain is the relation of inclusion as this:

$X_{0} ⊊ X_{1} ⊊ ... ⊊ X_{n}$

We have seen that for a prime ideal P, the affine algebraic set $V (P)$ is an irreducible closed subset. Hence we define a kind of dimension related to prime ideals. For a prime ideal $p$ , we can construct the chain of prime ideals with length n of the form

$p_{0} ⊊ p_{1} ⊊ ... ⊊ p_{n} = p$

with prime ideals $p_{0}$ ,..., $p_{n}$ . The chain is not necessarily unique, and we denote the maximum of the length of chains by height ( $p$ ). The Krull dimension of a ring is the maximal length of the possible chains of prime ideals in $A$ . We denote it by dim_k(A)

Recall that for two prime ideals such that $p \subset q$ , $V (p) \supset V (q)$ ; the inclusion is reversed.

Example 4.22 We have dim_k ℝ[x_1,x_2,...,x_n]=n, because the maximal chain of primes ideals is given by $(0) \subset (x_{1}) \subset (x_{1}, x_{2}) \subset ... \subset (x_{1}, x_{2}, ..., x_{n})$

One often refers to the Krull dimension of the residue class ring $R / I$ by “dimension of the ideal I”. The smallest prime ideal $p_{0}$ ideal is I itself (when I is prime) or a minimal $p_{0}$ including I (as one might study a non-prime ideal I), and the dimension counting ascends from $p_{0}$ as the start-point.

Example 4.23 Consider $I = (x y)$ in $R = ℝ [x, y]$ . This ideal is not prime. In order to count the dimension of the ideal I, the chain of primes is given by $(x) \subset (x, y)$ or $(y) \subset (x, y)$ , since $(x)$ and $(y)$ are the minimal prime ideals over $(x y)$ . Hence $\dim (R / I) = 1$ .

Example 4.24 Let f be a polynomial in the ring $S$ of dimension n, (say, $ℝ [x_{1}, x_{2}, ..., x_{n}]$ ). We assume that f is not the zero divisor, i.e. there is no element $g \in S$ such that $g \cdot f = 0$ and that it is not invertible, namely, there is no element g∈S such that $g \cdot f = 1$ . Then $R / (f)$ has dimension n-1. A simple example is $ℝ [x, y] / (x - y)$ , which is the line defined by the equation $y = x$ .

These examples seem to be trivial but demand us a certain amount of technical proof to show the validity of the statements. (See the argument in [5].)

As we have seen, an ideal I in a ring $R [x_{1}, x_{2}, ..., x_{n}]$ is defined by the set of polynomials. The points $(x_{1}, x_{2}, ..., x_{n}) \in R$ , which are the zero of the generating polynomials, determine the affine algebraic set $V (I)$ . If the affine algebraic set $V (I)$ is a discrete set, the ideal I is said to be “zero-dimensional”. If we have to solve the set of polynomials, we have to work with the zero-dimensional ideal, where we shall find the solution as the discrete set of points. It is fairly difficult to find the zero-set for general cases. Hence it is important to foresee whether an ideal is zero-dimensional or not. The criterion for an ideal to be zero-dimensional is given by Gröbner basis theory, which we shall see later.

Assume that k is an algebracally closed field.

Theorem 4.1 Weak Nullstellensatz Let $I \subset k [x_{1}, ... x_{n}]$ be an ideal (different from $k [x_{1}, ..., x_{n}]$ itself), then $V (I)$ is nonempty.

Theorem 4.2 (Nullstellensatz) Let $I \subset k [x_{1}, ... x_{n}]$ , then $I (V (I)) = \sqrt{I}$ .

As the set of polynomials define the geometric objects, we can adopt a view of geometry. In this section, we see a bit of it.

We say that a variety is irreducible when it is not empty and not the union of two proper sub-varieties, namely, $X = X_{1} \cup X_{2} for X_{1} and X_{2} \Rightarrow X = X_{1} or X = X_{2}$ .

For a prime ideal P in a ring S, is irreducible.

For a ring , we define the ring spectrum by

Spec(A) = {prime ideals of A}

For $A = K [x_{1}, ..., x_{n}] / J$ there is a one-to-one correspondence between Spec( $A$ ) and irreducible sub-varieties of $V (J)$ .

$Spec (A) \leftrightarrow {irreducible sub-varities V (J)} .$

Every maximal ideal (hence being prime) in $A = K [x_{1}, ..., x_{n}] / I$ with an algebraically closed field $K$ (such as $ℂ$ ) and an ideal I has the form $(x - a_{1}, ..., x - a_{n})$

for some point $(a_{1}, ..., a_{n}) \in V (I)$ . (Notice that, in case of $I = (0)$ , $V (I) = K^{n}$ .)Hence there is a one-to-one correspondence

$V (J) \leftrightarrow m-Spec$

by means of

$(x - a_{1}, ..., x - a_{n}) \leftrightarrow (a_{1}, ..., a_{n})$

The Zariski topology of a variety $X$ is defined by assuming that the sub-varieties $Y \subset X$ are the closed sets, whereby the union and the intersection of a family of variety are also closed sets. For an algebraically closed field $K$ , these two statements are valid.

(i) Any decreasing chain $V_{1} \supset V_{2} \supset \dots$ of varieties in $K^{n}$ eventually terminates.
(ii) Hence any non-empty set in $K^{n}$ has a minimal element.

A variety which satisfies the descending chain condition for closed subsets is called to be Noetherian. Observe that the chain for the Noetherian varieties is descending, while the chain for the ideals is ascending when we have defined the Noetherian ring.

We define another type of topology in Spec( $A$ ): the Zariski topology of Spec( $A$ ), in which the closed sets are of the form

$V (I) = {P \in Spec (A) | P \supset I}$

Two types of Zariski topology for varieties and Spec( $A$ ) have similar properties. The comparison is given in Chapter 5 of the book of Reid [4].

Definition 4.7 An integral domain is a non-zero commutative ring in which the product of any two non-zero elements is non-zero.

Example 4.25 $ℝ [x_{1}, ..., x_{n}]$ and $ℂ [x_{1}, ..., x_{n}]$ are integral domains.

Definition 4.8 A unique factorization domain (UFD) is an integral domain in which any nonzero element has a unique factorization by the irreducible elements in the ring.

Example 4.26 $ℤ$ is a UFD.

Example 4.27 For a field $F$ , $F [x]$ is a UFD.

Example 4.28 For a UFD $R$ , $R [x]$ is a UFD. By induction, $R [x_{1}, ..., x_{n}]$ is a UFD.

By the last example, $ℝ [x_{1}, ..., x_{n}]$ and $ℂ [x_{1}, ..., x_{m}]$ are UFDs. Hence any polynomial in these rings has unique factorization. However there are a lot of example which is not a unique factorization domain.

Example 4.29 $R [X, Y, Z, W] / (X Y - Z W)$ is not a UFD, since it permits two different factorization for one element: $a = X Y = Z W$ .

In the computation of molecular orbital theory through computer algebra, as is presented in the introduction, we approximate the energy function by polynomials. We simply replace the transcendental functions in the energy functional (such as $exp (A x)$ or $e r f (B x)$ with the corresponding formal power series, and we truncate these series at the certain degree. For this purpose, we execute Taylor expansion for the variable at a certain center point in the atomic distance. If we increase the maximum degree in Taylor expansion toward the infinity, the computation would converge to that by the exact analytic energy functional. Such a circumstance could be represented in a formal language of mathematics.

We need several definitions in order to present the formal description of Taylor expansion.

For a ring S, a “filtration” by the powers of a proper ideal I would be written as follows:

$F^{0} S (: = S) \supset F^{1} S (: = I) \supset F^{2} S \supset \dots \supset F^{n} S (: = I^{n}) \supset \dots$

The sequence is given by the inclusion relation. The filtration determines the Krull topology of I-adic topology. An “inverse system” is a set of algebraic objects ${(A_{j})}_{j \in J}$ , which is directed by the index J with an order $\leq$ . In the inverse system, we have a family of map (homomorphism),

$f_{i j} : A^{j} \to A^{i}$ for all i ≤ j

$f_{i i} = 1$

and

$f_{i k} = f_{i j} ο f_{j k}$ i ≤ j ≤ k

Let $S = ℝ [x_{1}, x_{2}, \dots, x_{n}]$ and $I = (x_{1}, x_{2}, \dots, x_{n})$ . The $F^{i} S (: = I^{i})$ is the ideal in $R$ , generated by the monomials of degree $i$ in $S$ . We also assume that the inclusion is given in the sense of ideal so that ideals generated by monomials of lower degrees should contain those generated by monomials of higher degrees. We set $A_{i} = S / F^{i} S$ by the quotient rings. Hence the entries in $A_{i} = S / F^{i} S$ are the finite polynomials, in which the monomials in $F^{i} S$ are nullified, and $A_{i}$ are represented by the set of polynomials up to degree $i - 1$ . The operation of the map from $S / F^{j} S$ to $S / F^{i} S$ is to drop the monomials of higher degrees and to shorten polynomials. In case of the polynomial approximation by means of Taylor expansion, the map is the projection from finer to coarser approximations.

The inverse system can be glued together as a mathematical construction, which is called the “inverse limit” (or “projective limit”). The inverse limit is denoted and defined as

$A = \lim_{\leftarrow} A_{i} = {(a_{j}) j \in J \in \prod_{j \in J} A_{i} | a_{i} = f_{i j} (a_{j}) f o r a l l i \leq j}$

The inverse limit A has the natural projection $π : A \to A_{i}$ (by which we can extract $A_{i}$ ).

The inverse limit is a “completion” of the ring $S = ℝ [x_{1}, x_{2}, \dots, x_{n}]$ with respect to $I = (x_{1}, x_{2}, \dots, x_{n})$ , when the inverse limit is taken for the quotient rings in the following way:

${\hat{S}}_{I} = lim_{\leftarrow} (S / I^{n} S)$

${\hat{S}}_{I}$ is the ring of formal power series $R [[x_{1}, x_{2}, \dots, x_{n}]]$ , and we can arbitrarily approximate the formal power series by some finite polynomials through the natural projection.

Example 4.30 Consider $exp (x)$ . Let $S = ℝ [x]$ and $I = (x)$ . $F S^{j}$ is the set of polynomials of the form $x^{j} f (x) .$ The Taylor expansion $exp (x)$ up to degree $j - 1$ , $1 + x + (1 / 2) x^{2} + \dots (1 / (j - 1)!) x^{j - 1}$ , lies in $F / F S^{j}$ . In the inverse limit of $A_{i}$ , namely, $ℝ [[x]]$ , the formal power series of $exp (x)$ , $1 + x + (1 / 2) x^{2} + \dots + (1 / n!) x^{n} + \dots$ is defined.

We can assume the formal power series in $R [[x_{1}, x_{2}, \dots, x_{n}]]$ would represent the inverse limit of “glued” Taylor expansions. In the algebraic formulation of molecular orbital theory, by means of inverse limit, we can bundle the different level of polynomial approximation with respect to the maximum polynomial degrees. Hence the natural map π means the model selection.

Such a mathematical formality might appear only to complicate the matter in practice, but it is important to introduce a neat “topology” in theory. The topology is constructed as follows: an object (i.e. a polynomial) s in a ring S has the nested (or concentrated) neighborhoods in ; the open basis of the neighborhoods is generated by the powers of a proper ideal $I \subset S$ and represented as

$x + I^{n} S for x \in S$

We say “open basis” in the sense of topology. If the reader is unfamiliar with topology, simply image that polynomials around a polynomial are sieved into different classes, which are represented by the above form. The powers of the ideal $I$ serve as the indicator of the distance between polynomials. In the terminology of topology, the completion makes a “complete” topological space. If we consider the inverse system for Taylor expansions at a point $X$ , the formal neighborhoods of $X$ should be small enough so that Taylor series should be convergent.

Example 4.31 Consider the map from $ℝ [x] / x^{n + j} ℝ [x]$ to $ℝ [x] / x^{j} ℝ [x]$ and the corresponding inverse system. Now $S = ℝ [x]$ and $F^{i} S = (x^{i}) ℝ [x]$ . A polynomial $f$ in $ℝ [x]$ has the open basis of neighborhoods, which is given by the set of the form

$f + x^{n} ℝ [x]$

The extension to the multivariate case in $ℝ [x_{1}, x_{2}, \dots, x_{n}]$ is straightforward.

We interpret the neighborhoods of in the slightly different view. Any polynomial has the image in each of $ℝ [x] / x^{j} ℝ [x]$ . Hence there are the different classes of polynomials around , which are represented by nil-potent ε as follows,

${0 + a ε such that ε^{2} = 0}$
${0 + a_{1} ε + a_{1} ε^{2} such that ε^{3} = 0}$

likewise,

${0 + \sum_{i = 1}^{n} a_{1} ε^{i} such that ε^{n + 1} = 0}$

Let $R = ℝ [x_{1}, ..., x_{n}]$ be a ring of polynomial functions. We can consider the rational function (or the fraction) $\frac{f (X)}{g (X)}$ for $f, g \in R$ . This sort of fraction is determined locally on a subset $X$ in $ℝ^{n}$ , such that $ℝ^{n} g (X) \neq 0$ . For a fixed point $a = (a_{1}, ..., a_{n}) \in X$ , we define the subset of such that $S = {p (a) \in R [x_{1}, ..., x_{n}] | p (a) \neq 0}$

Then, for the pair in $R \times S$ , denoted $(a, s)$ , the fraction $a / s$ can be well-defined, although it is a “local function”. The set of fractions must be closed under multiplication and addition. Moreover the equivalence relation between two pairs in $R \times S$ is given by $(a, s) \equiv (a', s') \Leftrightarrow a s' - a' s = 0.$

In commutative algebra, “localization” is defined in a more general way.

Definition 4.9 Let be a ring.

A subset $S \subset R$ is “multiplicatively closed” if $1 \in S$ and $a b \in S$ for all $a, b \in S$ .
For $R$ and its multiplicatively closed subset $S$ , the equivalence relation between two elements in $R \times S$ is given by

$(a, s) \sim (a', s') \Leftrightarrow there is an element u \in S such that u (a s' - a' s) = 0$

Then the set of equivalence classes

$S^{- 1} R : = {\frac{a}{s} | a \in R, s \in S}$

is the localization of at $R$ the multiplicatively closed subset S. It is a ring with addition and multiplication,

$\frac{a}{s} + \frac{a'}{s'} = \frac{a s' + a' s}{s s'}$

and

$\frac{a}{s} \cdot \frac{a'}{s'} = \frac{a a'}{s s'}$

Example 4.32 Let P be a prime ideal in a ring $R$ . As the set $R S = R \ P$ is multiplicatively closed, we localize $R$ by S. It is usually denoted by $R_{P}$ and called the localization of R at the prime ideal P. This localization has the exactly one maximum ideal $P R_{P}$ . In particular, for $R = ℝ [x_{1}, ..., x_{n}]$ and $P = {f \in R | f (a) = 0 for a point a \in ℝ^{n}}$ , $R_{P}$ is the set of rational functions well defined around $a$ .

Example 4.33 Let $R$ be a commutative ring and let $f$ be a non-nilpotent element in $R$ . A multiplicatively closed subset $S$ is given by ${f^{n} | n = 0, 1, ...}$ . The localization $S^{- 1} R = R [t] / (f t - 1) (= R [f^{- 1}])$ .

Example 4.34 Let $X = V (x y)$ (an affine algebraic set defined by the ideal $(x y)$ ). Consider the ring $A (X) = ℝ [x, y] / (x y)$ . For a point $a = (1, 0)$ in $x$ -axis, the function $y$ is equal to zero. So $y / 1$ and $0 / 1$ should be equivalent as the elements in $S^{(- 1)} R$ with $S = {f \in R | f (a) \neq 0}$ . Indeed $x \in S$ and $x (y \cdot 1 - 0 \cdot 1) = x y = 0$ in $A (X)$ , although $(y \cdot 1 - 0 \cdot 1) = y \neq 0$ in $ℝ [x, y]$ . Hence the equivalence between $y / 1$ and $0 / 1$ is proved. (This argument is not valid for $a = (0, 0)$ , because $x = 0$ at that point and it is not in $S$ .)

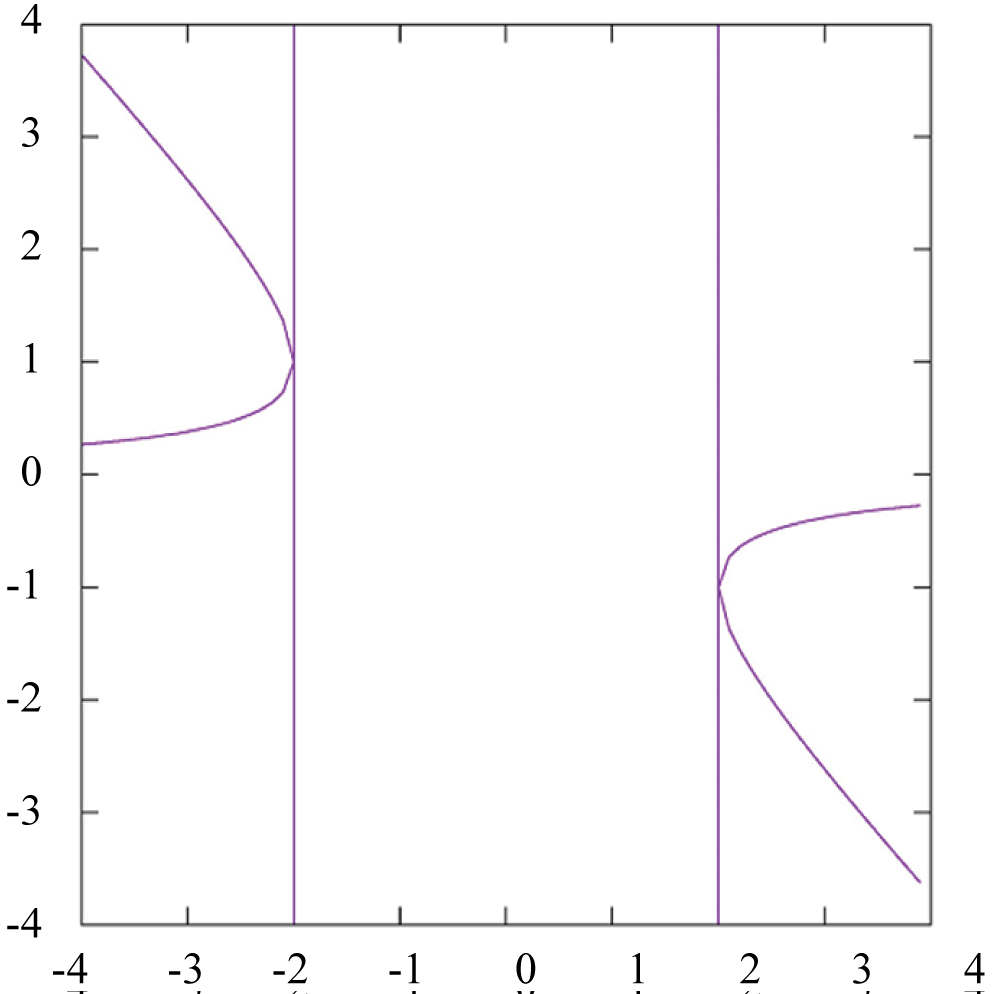
Example 4.35 Consider the secular equation $(\begin{matrix} 0 & - 1 \\ - 1 & 0 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = e (\begin{matrix} x \\ y \end{matrix})$

The roots are given by $(x, y, e) = (t, t, - 1), (t, - t, 1), (0, 0, 0)$ , and they lie in the affine algebraic set $V (I)$ by the ideal $I = (x + e y, y + e x)$ in $R = ℝ [x, y]$ . Let $P = (x, y, e + 1)$ and $S = R \ P$ . Since $I$ is represented by another basis set (by a Gröbner basis with lexicographic order $x > y > e$ ) as $I = (y (e^{2} - 1), x + e y)$ it follows that

$I \cdot S^{- 1} R = (y (e + 1), x + e y)$

because $e - 1$ is not in $P$ and it is an invertible element in $S^{(- 1)} R$ . The ideal $I \cdot S^{- 1} R$ describes “how the affine algebraic set $V (I)$ looks like” locally around the point $(x, y, e) = (0, 0, - 1)$ . Indeed, the eigenvalue $e$ is the root of the determinant $e^{2} - 1 = 0$ and the parabola $f = e^{2} - 1$ looks like $g = 2 (e + 1)$ locally around $e = - 1$ .

Consider the extension of quotient ring $R = K [x_{2}, ... x_{n}] / I_{1} \subset S = K [x_{1}, ... x_{n}] / I$

We say $\bar{x_{1}} = x_{1} + I \in S$ is integral over $R$ when it satisfies the following condition:

Definition 4.10 Let $R \subset S$ be a ring extension. An element $s \in S$ is integral over $R$ if it satisfies a monic polynomial equation $s^{d} + a_{1} s^{d - 1} + \dots + a_{d} = 0$ with $a_{i} \in R$ for all $i = 1, ..., d$ .

If every element in $S$ is integral over $R$ , then $S$ is integral over $R$ . We say that $S$ is the integral extension of $R$ . Then these statements hold:

Then these statements hold:

If $s_{1}, ..., s_{m} \in S$ are integral over $R$ , $R [s_{1}, ..., s_{m}]$ is integral over $R$ .
The succession of integral extensions makes the integral extension. If $S$ is integral over $R$ and $T$ is integral over S, then is $T$ integral over $S$ .

Example 4.36 $ℝ [y] \to ℝ [x, y] / (x y - 1)$ is not an integral extension. From the geometrical viewpoint, the correspondence by this map (by inverting the direction) gives us the projection of the hyperbola $x y = 1$ to $y$ -axis.

There is no point in $x y = 1$ which is projected to the point $y = 0$ in $y$ -axis, while any other points in $y$ -axis have a preimage in $x y = 1$ .

Example 4.37 Apply the change of coordinates to the above example: $x \to t$ and $y \to t + s$ . Then we obtain $ℝ [s] \to ℝ [t, s] / (t^{2} + t s - 1)$ , which is an integral extension. From the geometrical viewpoint, the correspondence between two rings gives us the projection to the hyperbola $t (t + s) = 1$ to $t$ -axis. One always finds two points in $t (t + s) = 1$ , namely, $((1 / 2) (s \pm \sqrt{s^{2} + 4}), s)$ , which are projected to an arbitrary point s in s-axis. The change of coordinates with polynomial maps of this sort (which might be non-linear) enables us to obtain an integral extension of a ring, even if the domain of the map is not an integral extension (Noether-normalization) [2].

Example 4.38 Consider the ideal $I = (x + e y, y + e x) \subset ℝ [x, y, e]$ . $I$ represents a simple secular equation $(\begin{matrix} 0 & - 1 \\ - 1 & 0 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = e (\begin{matrix} x \\ y \end{matrix})$ .

$ℝ [x, y] \to ℝ [e, x, y] / I$ is not an integral extension. In fact, $I$ can be represented by another basis $(- y + y e^{2}, x + y e)$ , but there is no monic equation for $e$ . One cannot find the point in $V (I)$ which is projected to the non-zero vector $(x, y)$ unless e takes certain particular values (the eigenvalues). This example is an application of integrality check by means of Gröbner basis. (This useful idea will be expounded later.)

Let us consider a curve $y^{2} = x^{3} + x^{2}$ in $ℝ [x, y]$ , as in Figure 2. The curve has a singularity at $(0, 0)$ where two branches intersect. Let $t = y / x$ . Then $y = t x$ , $y^{2} = x^{3} + x^{2}$ , and $t^{2} = (x + 1)$ . These equations make an ideal $I = (y - t x, y^{2} - x^{3} - x^{2}, t^{2} - x - 1)$ in $ℝ [x, y, t]$ . The affine algebraic variety $V (I)$ has no singularity and it maps to the curve $y^{2} = x^{3} + x^{2}$ by the projection to $ℝ [x, y]$ .

This is an example of the resolution of singularity. This sort of procedure lies in a broader concept of “normalization”. If $S$ is an integral domain, its normalization $\bar{S}$ is the integral closure of $S$ in the quotient field (the field of fractions) of $S$ .

Definition 4.11 (Normal) Let $S$ be an integral domain with the field of fractions $K$ . Let f be any monic polynomial in $S [x]$ . If every root $a / b \in K$ of f also lies in $S$ , then $S$ is normal.

Example 4.39 One can prove that every UFD is normal.

Definition 4.12 (Normalization) Let $R$ be a commutative ring with identity. The normalization of $R$ is the set of elements in the field of fractions of $R$ which satisfy some monic polynomial with coefficients in $R$ .

Example 4.40 Observe that, in the above example, $t$ is in the quotient field of $S = ℝ [x, y] / (y^{2} - x^{3} - x^{2})$ , and observe that the equation $t^{2} - x - 1$ is a monic polynomial which guarantees that t is integral over $S$ . In fact, in order to prove that this resolution of singularity is literally the normalization, it is necessary for us to do the argument in detail. So we omit it now.

Example 4.41 Consider $I = (x^{2} - y^{3})$ and $V (I)$ . By setting $x = t^{3}$ and $y = t^{2}$ , the coordinate ring $C [x, y] / I ≃ C [t^{3}, t^{2}]$ . Let us denote $ℂ [t^{3}, t^{2}]$ by $ℂ (V)$ . Then $t$ is a root of polynomial $s^{2} - t^{2}$ in $ℂ (V) [s]$ , and $t \notin ℂ (V)$ . Hence $ℂ (V)$ is not normal.

Example 4.42 In the above example of the resolution of singularity, t is contained in the normalization of $ℂ (V)$ . As t is the root of $s^{2} - t^{2} \in ℂ (V) [s]$ , every element of $ℂ [t]$ is also a root of some monic polynomial in $ℂ (V) [s]$ . (To prove the validity of this statement, we need some arguments by commutative algebra ) Hence, $ℂ [t]$ in the normalization of $ℂ (V)$ . Besides, $ℂ [t]$ is a UFD, hence normal. Therefore $ℂ [t]$ is the normalization of $ℂ (V)$ .

In fact, the procedure to find a normalization of $S = K [x_{1}, ..., x_{n}] / I$ is to find another ring $\bar{S} = K [y_{1}, ..., y_{m}] / I'$ with the normalization map $S$ ↪ $\bar{S}$ . The algorithm by Decker et al. enables us to compute such normalization. If $I \subset R = K [x_{1}, x_{2}, .... x_{n}] / I$ is a radical ideal, the normalization by the algorithm shall give the ideal decomposition of $I$ . The computation returns s polynomial rings $R_{1}, ..., R_{s}$ and s prime ideals $I_{1} \subset R_{1}, ..., I_{s} \subset R_{S}$ and s maps ${π_{i} : R \to R_{i}, i = 1, ... s}$ such that the induced map $π : K [x_{1}, ..., x_{n}] / I \to R_{1} / I_{1} \times \dots \times R_{s} / I_{s}$ , whereby the target of $π$ (the product of quotient rings) is the normalization.

As we shall see in section 6, the primary ideal decomposition is a substitution for the solution of eiganvalue problem. It is not so surprising that we meet again the decomposition of an ideal in the desingularization of the algebraic variety. The secular equation is given as

${a_{i 1} x_{1} + a_{i 2} x_{2} + \dots + a_{i n} x_{n} = ε x_{i}, i = 1, ... n}$

or

${0 = f_{i} (x_{1}, x_{2}, ..., x_{n}) : = a_{i 1} x_{1} + a_{i 2} x_{2} + \dots + a_{i n} x_{n} - ε x_{i}, i = 1, ... n}$

Then we have to find $ϵ$ which shall give the non-zero solution of the matrix equation

$(\begin{matrix} a_{11} - ε & a_{12} & \dots & a_{1 n} \\ a_{21} & a_{22} - ε & \dots & a_{2 n} \\ ⋮ & ⋮ \\ a_{n 1} & a_{n 2} & \dots & a_{n n} - ε \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ ⋮ \\ 0 \end{matrix})$

Observe that the matrix in the left-hand side is the Jacobian matrix

$J_{i j} = \frac{\partial f_{i}}{\partial x_{j}}$

The singular locus of the algebraic affine set defined by ${f_{i}}$ is determined by the rank condition of the Jacobian matrix, namely by the condition that the Jacobian matrix is not of full rank. The desingularization is the normalization, and the latter would result in the decomposition of an ideal, by the algorithm of Decker. It is not so difficult to trace the algorithm of normalization given in [10,11].

We need some definitions. Let $A = K [x_{1}, ..., x_{n}] / I$ . For $I = (f_{1}, ..., f_{m})$ The Jacobian ideal $Jac (I)$ is defined by the $c \times c$ minors of the matrix

$(\begin{matrix} \frac{\partial f_{1}}{\partial x_{1}} & \dots & \frac{\partial f_{1}}{\partial x_{n}} \\ ⋮ & ⋮ \\ \frac{\partial f_{m}}{\partial x_{1}} & \dots & \frac{\partial f_{m}}{\partial x_{n}} \end{matrix})$

Where, $c = n - dim (X)$ with $X = V (I)$ . Then the singular locus of $A$ is given by $sloc (A) = V (Jac (I) + I)$

Then we execute the computation by following these steps.

Compute the singular locus $I$ . Let $J$ be a radical ideal such that $V (J)$ contains this singular locus.
Choose a non-zero divisor $g \in J$ and compute $g J : J$ . For a homomorphism from $J$ to $J$ , denoted by $Hom (J, J)$ , and for a non-zero divisor $x$ in $J$ , $x Hom (J, J) = x J : J$ .
Let $g_{0} (: = g), g_{1}, ..., g_{s}$ be the generators of $g J : J$ . There are quadratic relations of the form $\frac{g_{i}}{g} \frac{g_{j}}{g} = \sum_{k = 0}^{s} ζ_{k}^{i j} \frac{g_{k}}{g}, with ζ_{k}^{i j} \in A$ .
Also there are linear relations between $g, g_{1}, ..., g_{s}$ (the syzygy) of the form $\sum_{k = 0}^{s} η_{k} \frac{g_{k}}{g} = 0$
Then a surjective map is given by $A [T_{1}, ..., T_{s}] ↠ Hom (J, J),$ ↠ $T_{i} ⇝ \frac{g_{i}}{g}$
The kernel of this map is an ideal $I_{1}$ generated by the quadratic and linear relations of the form $T_{i} T_{j} - \sum_{k = 0}^{s} ζ_{k}^{i j} T_{k}, \sum_{k = 0}^{s} η_{k} T_{k}$
and it yields the extension of $A$ by $A_{1} = A [T_{1}, ..., T_{s}] / I_{1}$
This ring $A_{1}$ may be normal. If not, we make the extension of $A_{1}$ again. After finite steps of the successive extensions, we arrive at the normalization.
• The criterion of normality: $A$ is normal if and only if $A = {Hom}_{A} (J, J)$ . If this criterion is satisfied, we do not have to add extra $T_{i}$ . Then the algorithm stops.

Consider $I = (x + e y, y + e x)$ in $ℚ [x, y, e]$ . Let $A = ℚ [x, y, e] / I$ . The Jacobian matrix of $I$ is $(\begin{matrix} 1 & e & y \\ e & 1 & x \end{matrix})$ .

Then $Jac (I) = (1 - e^{2}, x - e y, x e - y)$ , or more simply $(1 - e^{2}, x, y)$ , and $sloc (A) = V (Jac (I) + I) = V (1 - e^{2}, x, y)$ . (Recall that the Gröbner basis of I is ${x (e^{2} - 1), y + x e}$ .) Hence we set $J = (1 - e^{2}, x, y)$ as a radical ideal containing the singular locus. Choose $x$ as the non-zero divisor in $J$ . Then $x J = (x^{2}, x y)$ , since $x (1 - e^{2})$ vanishes as an element in $A$ . Hence, $x J : J = (x, y)$ . Let $T = y / x$ .

Then there are two linear relations

$e + T = 0, e T + 1 = 0$

and a quadratic relation

$T^{2} = \frac{y^{2}}{x^{2}} = e^{2}$

We have the extended ring

$\begin{array}{r} A' & = & A [T] / (e + T, e T + 1, T^{2} - e^{2}) \\ = & ℚ [x, y, e, T] / (x + e y, y + e x, y - T x, e + T, e T + 1, T^{2} - e^{2}) \end{array}$

with the ideal $I' = (x + e y, y + e x, y - T x, e + T, e T + 1, T^{2} - e^{2})$ . This ring $A'$ is normal. Indeed, after some algebra (in fact, by means of computer algebra), we can check that the singular locus of $V (A')$ is an empty set.

(We check the emptiness by the computation of Gröbner basis, which should be generated by $(1)$ .) From this reason, for a radical ideal $J$ which contains the singular locus, we have $J = A'$ (the ring itself). Hence ${Hom}_{A'} (J, J) = A'$ and the criterion for the normality is satisfied.

As $T$ is integral over $A$ and actually $T = \pm e$ in $A$ , the ideal $I'$ is represented in two ways by the substitution for $T$ :

$I_{a} = (x + e y, y + e x, y - e x, e, e^{2} + 1) = (1)$

$I_{b} = (x + e y, y + e x, 1 - e^{2}) = (x + e y, 1 - e^{2})$

These two ideal lie in $ℚ [x, y, e]$ . As $I_{a}$ is trivial, we adopt $I_{b}$ for the purpose of normalization. In addition, when we introduce the variable $T$ , we implicitly assume that $x \neq 0$ . When $x = 0$ , the ideal $I$ is given by

$I_{0} = I \cap^{} (x) = (x, y)$

Then the normalization of is given by two rings:

$ℚ [x, y, e] / I_{0} = ℚ [x, y, e] / (x, y)$

and

$ℚ [x, y, e] / I_{b} = ℚ [x, y, e] / (x + e y, 1 - e^{2})$

Compare this result to the example of primary ideal decomposition with the same ideal $I$ which we will compute in section 6. We observe that the normalization has done the decomposition of the ideal imperfectly.

Consider the problem to solve the equation
$f (x) = x^{2} - 7 = 0$
Let us substitute $a_{0} = 1$ in $f (x)$ :
$f (1) = - 6 \equiv 0 m o d 3$
Let $a_{1} = 1 + 3 s$ . Then
$f (a_{1}) \equiv - 6 + 6 s m o d 3^{2}$
Hence, if $s = 1$ , then
$f (a_{1}) \equiv - 6 + 6.1 = 0 m o d 3^{2}$
Let $a_{2} = 1 + 3 \cdot 1 + 3^{2} s$ . Then
$f (a_{2}) \equiv 9 + 72 s m o d 3^{3}$
Hence, if $s = 1$ , then
$f (a_{2}) \equiv 9 + 71.1 \equiv 0 m o d 3^{3}$

Likewise, by setting $a_{n} = a_{n - 1} + 3^{n} s$ , we can determine s such that $f (a_{n}) \equiv 0 m o d 3^{n + 1}$ . It means that we obtain the 3-adic solution of the equation

$X = a_{0} + 3 \cdot a_{1} + 3^{2} \cdot a_{1} + \dots$

Let us consider the polynomial $f (X)$ in $ℤ_{p} [x]$ . We have

$f (X + p^{n} Y_{n}) = f (X) + p^{n} Y_{n} f^{'} (X) m o d p^{n + 1}$

Hence if $p^{n} f^{'} (X)$ ≢ $0 \mod p^{n + 1}$ or, equivalently, if $f^{'} (α)$ ≢ $0 m o d p$ , we obtain $Y$ such that $f (X + p^{n} Y) \equiv 0 \mod p^{n + 1}$ by the fraction.

$Y_{n} = - \frac{f (X)}{f' (X)}$

Observe the similarity with Newton method in numerical analysis. In other words, the p-adic solution of $f (x) = 0$ as $\sum_{i = 0}^{\infty} p^{i} Y_{n}$ . This is Hensel’s lemma, stated as follows.

Theorem 4.3 (Hensel’s lemma) If $f (x) \in ℤ_{p} [x]$ and $a \in ℤ_{p}$ satisfies

$f (a) \equiv 0 \mod p$

and

$f^{'} (a)$ ≢ $0 \mod p$

then there is a unique $α \in ℤ_{p}$ such that $f (α) = 0$ and $α \equiv a \mod p$ .

In the lemma, there is a condition $f^{'} (α)$ ≢ $0 m o d p$ , while, from the above example, it seems that we should use $f^{'} (a_{n})$ ≢ $0 m o d p$ for changeable $a_{n}$ . In fact, by the construction, $a_{n} \equiv a_{0} = a m o d p$ , it follows that $f' (a_{n}) \equiv f' (a)$ . Hence we assume that condition only for the starting point $a$ .

In commutative ring there is a related idea, called “Linear Hensel Lifting”, by the following theorem.

Let be a commutative ring. Let $f$ , $g_{0}$ , $h_{0}$ be univariate polynomials in $R [x]$ and let $m$ be a ideal in $R$ . If $f$ decomposes into the product of $g_{0}$ and $h_{0}$ in $R / m$ , that is to say,

$f \equiv g_{0} h_{0} m o d m$

and if there exist polynomials s and t in $R [x]$ such that

$s . g_{0} + t . h_{0} \equiv 1 m o d m$

then, for every integer $l$ we have polynomials $g^{(l)}$ and $h^{(l)}$ such that

$f \equiv g^{(l)} h^{(l)} \mod m^{l}$

and

$g_{0} \equiv g^{(l)}, h_{0} \equiv h^{(l)} \mod m$

The computation of $g^{(l)}$ and $h^{(l)}$ is done in a constructive way.

Let $g^{(1)} = g_{0}$ and $h^{(1)} = h_{0}$ . And let

$g^{(l + 1)} = g^{(l)} + m^{l} q_{g}$

and

$h^{(l + 1)} = h^{(l)} + m^{l} q_{h}$

We solve the equation

$g_{0} q_{h} + h_{0} q_{g} \equiv \frac{f - g^{(l)} h^{(l)}}{m^{(l)}} \mod m$

so that we obtain $q_{g}$ and $q_{h}$ such that $deg (q_{g}) < deg (g_{1})$ and $deg (q_{h}) < deg (h_{1})$ .

Example 4.44 $f (x) = x^{2} - (1 + t)$ , and $R = ℂ [[t]]$ . For $m = (t) \subset R$ , we begin from

$g_{0} = x + 1$
$h_{0} = x + 1$

and we obtain $g^{(l)}, h^{(l)}$ in an iterative way. As usual, we simply write the roots of $f (x) = 0$ by $\pm \sqrt{1 + t}$ .

Hensel’s lemma implies the existence of a power series in $ℂ [[t]]$ .

The computation of hydrogen molecule, presented in the introduction, is done in the real number, and in the algebraic set defined by the polynomials:

$A = {p_{i} (x_{1}, x_{2}, .. x_{n}) = 0 | i = 1, ... r}$

On the other hand, we can add extra constraint of the form

$B = {q_{i} (x_{1}, x_{2}, .. x_{n}) \geq 0 | i = 1, ... s}$

Hence it is important to study the existence of solutions of (A) with (B).

We review several results from real algebraic geometry from now on. (As for rigorous theory, see the book by Bochnak et al. [12] or the book by Lassere [13].)

These two statement are equivalent for an affine algebraic variety:
(i) the ideal $I (X)$ has real generators $f_{1}, ..., f_{k} \in ℝ [x_{1}, ..., x_{n}]$ .
(ii) $X = \bar{X}$ , (by complex conjugation)

Then we define real affine algebraic variety and real ideal.

Definition 4.13 The set of real points $V_{ℝ} (f_{1}, ..., f_{k})$ with $f_{i} \in ℝ [x_{1}, ..., x_{n}]$ is called a real affine algebraic variety.

Definition 4.14 An ideal $I$ is called as a real ideal, if it is generated by real generators and satisfies the following property:

$a_{i} \in ℝ [x_{1}, ..., x_{n}] and a_{2}^{2} + ... + a_{p}^{2} \in I \Rightarrow a_{i} \in I$

For any real algebraic variety, $I (X)$ is a real ideal. To see the difference between real and non-real ideals, consider $(x)$ , $(x^{2})$ , and $(1 + x^{2})$ . The last two ideals are not real ideals.

Definition 4.15 Let $p_{1}, ... p_{r} \in ℝ [x_{1}, x_{2}, ..., x_{n}]$ polynomials. The set $W (p_{1}, ..., p_{r}) = {a \in ℝ^{n} | p_{1} (a) \geq 0, ... p_{1} (a) \geq 0}$ is called as a basic closed semi-algrbraic set. A general semi-algebraic set is the boolean combination of them.

Theorem 4.5 (Real NullStellensatz) Let us define the real radical as follows:

$\sqrt[ℝ]{I} = {p \in ℝ [x] | p^{2 m} + \sum_{j} g_{j}^{2} \in I for some q_{j} \in ℝ [x], m \in ℕ \ 0}$

Then it holds that $\sqrt[ℝ]{I} = I (V_{ℝ} (I))$ , where $V_{ℝ} (I)$ is the real affine algebraic set of $I$ . If $J$ is a real ideal, $\sqrt{J} = I (V_{ℝ} (J))$ ; that is to say, for a real ideal $J$ , the radical ideal $\sqrt{J}$ (by the standard definition of commutative algebra) is equal to the ideal of $V_{ℝ} (J)$ (the affine algebraic set of $J$ in $ℝ$ ).

Example 4.45 For $I = (x^{2} + y^{2})$ , $I (V_{ℝ} (I)) = (x, y)$ .

$\sum ℝ [x]^{2} = {p \in ℝ [x] | p = \sum_{i = 1}^{r} q_{i} {(x)}^{2} for some r \in ℕ}$

$Σ^{2} (g_{1}, ..., g_{n}) = {\sum_{e \in {0, 1}^{r}} σ_{e} g_{1}^{e_{1}} ... g_{1}^{e_{r}} | σ_{e} \in \sum ℝ [x]^{2}}$

$M (f_{1}, ..., f_{m}) = {f_{1}^{e_{1}} f_{2}^{e_{2}} ... f_{m}^{e_{m}} | e_{1}, ..., e_{m} \in ℕ}$

From these definitions, $ℝ {[x]}^{2}$ are the sums of squares of polynomials; $Σ^{2} (g_{1}, ... g_{n})$ is the “quadratic module”, which is the set of polynomials generated by $ℝ {[x]}^{2}$ and $g_{1}, ..., g_{n}$ ; M is the multiplicative monoid generated by $f_{1}, ..., f_{m}$ .

Theorem 4.6 (Positivestellensatz) Let ${g_{k} | k = 1, ..., n}$ , ${f_{i} | i = 1, .. m}$ , and ${h_{l} | l = 1, ... t}$ be the polynomials in $ℝ [x_{1}, ..., x_{n}]$ . The following properties are equivalent.

(i) ${x \in ℝ^{n} | \begin{array}{l} g_{k} (x) \geq 0, k = 1, ..., n \\ f_{i} (x) \neq 0, i = 1, ..., m \\ h_{i} (x) = 0, l = 1, ..., t \end{array}}$

(ii) $\exists g \in Σ^{2} 〈 g_{1}, ... g_{n} 〉$ , $\exists f \in M (f_{1}, ... f_{m})$ , and $\exists h \in I (h_{1}, ... h_{l})$ such that $g + f^{2} + h = 0$ . From this theorem, one can derive the following theorem, also.

Theorem 4.7 Let $f$ and ${g_{k} | i = 1, ..., n}$ be polynomials in $ℝ [x]$ and $K = {x \in ℝ ∣ x \in W (g_{1}, .., g_{n})}$ . Then the following statements hold.

(i) $\forall x \in K, f (x) \geq 0$ if and only if $\exists p \in ℕ, \exists g, h \in Σ^{2} (g_{1}, ... g_{n})$ such that $f g = f^{2 p} + h$ .

(ii) $\forall x \in K, f (x) > 0$ if and only if $\exists p \in ℕ, \exists g, h \in Σ^{2} (g_{1}, ... g_{n})$ such that $f g = 1 + h$ .

The theorem asserts that
$f > 0$
$f > 0$
$q^{2} f = p_{1}^{2} + \dots + p_{n}^{2}$

for some polynomials $q, p_{1}, ..., p_{n}$ . (From the theorem, the set ${x \in ℝ | - f (x) \geq 0, f (x) \neq 0}$ is empty if and only if $\exists u = s_{1}^{2} + \dots + s_{n - 1}^{2} - f q^{2} \in Σ^{2} (- f)$ , $\exists p \in ℕ$ , $\exists v = f^{p} \in M (f)$ , such that $u + v^{2} = 0$ . Now we can choose $p_{1} = s_{1}, ..., p_{n - 1} = s_{n - 1}, p_{n} = f^{p}$ .) In other words, every non-negative polynomial is a sum of squares of rational functions.

Example 4.47 Consider $x^{2} + a x + b = 0$ .
Define $D$ , $f$ , $g$ , $h$ to be
$D = b - a^{2} / 4$
$g = {(\frac{1}{\sqrt{D}} (x + \frac{a}{2}))}^{2}$
$f = 1$
$h = - \frac{1}{D} (x^{2} + a x + b)$

When $D > 0$ , these polynomials are well defined in $ℝ [x]$ . Then it happens that $g + f^{2} + h = 0$ , where $1 = f \in Monoid ({1})$ , $g \in \sum^{} ℝ {[x]}^{2} \subset Σ^{2} ({1})$ ,and $h \in I (x^{2} + a x + b)$ . In other words, the quadratic equation has no real root if and only if $D > 0$ .

Example 4.48 Consider the secular equation (for a molecular orbital model of a simple diatomic molecule):

$(\begin{matrix} 0 & - 1 \\ - 1 & 0 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = e (\begin{matrix} x \\ y \end{matrix})$

The problem is equivalent to

$\begin{array}{r} h_{1} = x + e y & = & 0 \\ h_{2} = y + e x & = & 0. \end{array}$

Add the constraint:

$f = x - y \neq 0$

A Gröbner basis (with respect to the lexicographic order $x > y > e$ ) of the ideal $I = (h_{1}, h_{2})$ is $H = (y e^{2} - y, x + y e)$ . After some algebra, $f^{2}$ reduces to $2 y^{2} e + 2 y^{2}$ with respect to $H$ . Hence we have obtained

$g + f^{2} + h = 0$ for $h \in I (h_{1}, h_{2})$ and $g = - 2 (e + 1) y^{2}$ . If $e \leq - 1$ , $g = {(\sqrt{- 2 (e + 1)} y)}^{2}$ and it satisfies the condition of Positivstellensatz. Hence there is no real solution to the problem. (Or we say that the non-symmetric wave function $(x, y)$ such that $x \neq y$ is not the ground state of the molecule at eigenvalue $- 1$ .)

Let $R \subset S$ be a ring extension. Remember how can be an element integral over $R$ .

Definition 4.17 An element $s \in S$ is integral over $R$ if it satisfies a monic polynomial equation with coefficients
${r_{i} \in R}$
$s^{d} + r_{1} s^{d - 1} + \dots + r_{d} = 0$

The equation is called an integral equation for s over $R$ . If every element $s \in S$ is integral over $R$ , we say that $S$ is integral over $R$ . We also say that $R \subset S$ is an integral extension.

Definition 4.18 Let $S$ be an affine ring $S = K [x_{1}, ..., x_{n}] / I$ . Then there are elements $y_{1}, ..., y_{d} \in S$ with the following properties.

(i) $y_{1}, ..., y_{d}$ are algebraically independent over $K$ .

(ii) $K [y_{1}, ..., y_{d}] \subset S$ is an integral ring extension.

If the elements y₁,...,y_d satisfy these two conditions, the inclusion $K [y_{1}, ..., y_{d}] \subset S$ is a Noether normalization for $S$ .

Example 4.49 Let $I = (x + e y, y + e x) \subset ℝ [x, y, e]$ , and let $S = ℝ [x, y, e] / I$ . The residuals $\bar{x}, \bar{y} (\in S)$ are not integral over $ℝ [e]$ . But the change of the variables

$x \to x, y \to y' = 4 x + y, e \to 5 x + 6 y + e$

makes the change in as follows:

$I \to I^{'} = (20 x^{2} + 29 x y + 4 x e + x + 6 y^{2} + y e, 5 x^{2} + 6 x y + x e + 4 x + y)$

We can prove the residuals $\bar{x}, \bar{y'} (\in S' = ℝ [x, y', e'] / I'$ ) are integral over $ℝ [e']$ . Indeed, after a hard algebra (by means of Gröbner basis theory and the variable elimination as we learn later), we affirm that the ideal $I'$ contains following two polynomials

$65 y^{3} + 28 y^{2} e + 2 y^{2} + 3 y e^{2} - 3 y$

and

$325 x^{3} - 38 x^{2} e - 12 x^{2} + x e^{2} - x$

Example 4.50 There are several types of the variable change which conduct Noether normalization.

$x_{i} \to y_{i} = x_{i} + λ_{n} x_{n}$ with $λ_{i}$ in the coefficient field $K$ , when $K$ is an infinite field.
$x_{i} \to y_{i} = x_{i} - x_{i}^{r^{i - 1}} for 2 \leq i \leq n$ . We have to find an integer $r$ .

To do with the latter type is, in fact, the proof of the existence of Noether normalization. Let $f (x_{1}, ..., x_{n})$ be a polynomial defining the ideal $I$ . By the change of variables, we obtain

$f (x_{1}, y_{2} + x_{1}^{r}, ..., y_{n} + x_{1}^{r^{n - 1}})$

If the monomial of the highest degree with respect to $x_{1}$ is originally given by

$A x_{1}^{a_{1}} x_{2}^{a_{2}} \dots x_{n}^{a_{n}}$

it becomes

$A x_{1}^{a_{1}} \prod_{i = 2}^{n} (y_{i} + x_{1}^{r^{i - 1}})$

Hence, after the change of the variables, the term of the highest degree with respect to $x_{1}$ is given by $x_{1} A x_{1}^{a_{1} + a_{2} r^{2} + \dots + a_{n} r^{n - 1}}$

If r is large enough, this term has the degree larger than any other monomials. Therefore $x_{1}$ is integral over $K [y_{2}, ..., y_{n}]$ . There is another way to define the dimension of the variety. Let $I \in K [x_{1}, ..., x_{n}]$ be a proper ideal. Let $A = V (I)$ . If $K [y_{1}, .., y_{d}] \in K [x_{1}, ..., x_{n}] / I$ is a Noether normalization, the dimension of $A$ is given by the number $d$ , namely, $d i m (A) = d$

One of the important ideas concerning algebraic geometry, differential algebra, and quantum mechanics is the differential Galois theory.

Let us solve

$y' - y = 0$

We get $C exp (t)$ .

Let us solve

$y ″ + 2 t y' = 0$

We get $C \int^{} d t exp (- t^{2})$ . In the first case, we can get the solution in the range of elementary functions; on the other hand, in the second case, we have to do the integration.

Then there arises a question: under what circumstance one can express the solution of a differential equation using exponents, integration, and also by adding algebraic elements? We proceed step by step, by adding more elements which are constructed over the elements already presented in the computation. The analytic solution given by this way is called Liouvillian solution, although it is not always possible to construct it. The solvability condition is given by the differential Galois theory [14-16].

In the application of eigenvalue problem in quantum mechanics, we can consider the one-dimensional Schrödinger equation:

$ψ ″ (x) = (P_{2 n} (x) - λ) ψ (x)$

with the even-degree monic polynomial potential

$P_{2 n} (z) = z^{2 n} + \sum_{i = 0}^{2 i - 1} a_{i} z^{i} = {(z^{n} + \sum_{i = 0}^{i - 1} b_{i} z^{i})}^{2} + \sum_{i = 0}^{n - 1} c_{i} z^{i}$

In the last representation of $P_{2 n}$ , the polynomial is given by completing squares. Let us write the solution in the following form:

$ψ (x) = P_{s} exp (\pm f (x))$

as the product of a monic polynomial $P_{s}$ and

$f (x) = \frac{x^{n}}{n + 1} + \sum_{k = 0}^{n - 1} \frac{b_{k} x^{k + 1}}{k + 1}$

Now we can establish the relation among the coefficients ${b_{i}}$ and ${c_{i}}$ in the polynomial potential, the eigenvalue $λ$ and $P_{s}$ . The relation of this sort is given by a second-order differential equation for $P_{s}$ . As the consequence of differential Galois theory, the equation has solutions at the particular setting of ${b_{i}}$ , ${c_{i}}$ and $λ$ . To solve the problem, one can utilize Gröbner basis theory and the variable elimination, which shall be explained later. If the equation is solvable, we can obtain the analytic solution [16].

It is advisable that the readers should consult textbooks and grasp the concepts of more advanced technical terms, such as “module”, “free module”, ”regular local rings”, “valuation”, “Artinian ring”, “affine algebraic variety”, or so. Maybe the concepts of homological algebra would be necessary, such as “functor”, “exact sequence”, “resolution”, “projective”, “injective”, “Betti-number”, and so on. Indeed, the research articles are frequented by these concepts.

The Gröbner basis theory is the key technique of commutative algebra and algebraic geometry[17-19]. The idea was first proposed by Bruno Buchberger, and the namesake is his advisor Wolfgang Gröbner.

In one-variable case, we implicitly use the “monomial order” through the ordering of degrees: $1 < x < x^{2} < \dots$ or $1 > x > x^{2} > ...$ . In the multivariate case, we encounter the monomials of the form xⁱ y^j z^k. What should be the appropriate ordering of the monomials? In fact, there are several ways to set the order .

Let $x^{a} (= x_{1}^{a_{1}} ... x_{n}^{a_{n}})$ and $x^{b} (= x_{1}^{b_{1}} ... x_{m}^{b_{m}})$ be the monomials. And let a and b be sequence of superscripts $(a_{1}, a_{2}, ..., a_{n})$ and $(b_{1}, b_{2}, ..., b_{n})$ .

Definition 5.1 The lexicographic order.

$x^{a} < x^{b} \Leftrightarrow \exists i (1 \leq i \leq n) : a_{n} = b_{1}, ..., a_{i - 1} = b_{i - 1}, a_{i} < b_{i}$

This definition is equivalent to the following statement.

$x^{a} < x^{b}$ , if the left-most component of a―b is negative.

Definition 5.2 The reverse lexicographic order.

$x^{a} < x^{b} \Leftrightarrow \exists i (1 \leq i \leq n) : a_{n} = b_{n}, ..., a_{i + 1} = b_{i + 1}, a_{i} > b_{i}$

This definition is equivalent to the following statement.

$x^{a} < x^{b}$ , if the right-most component of a―b is positive.

Definition 5.3 The degree reverse lexicographic order:

Let $\deg (x^{a}) = a_{1} + ... + a_{n}$

$x^{a} < x^{b} \Leftrightarrow$

(1) $\deg (x^{a}) < \deg (x^{b})$

or

(2) $\deg (x^{a}) = \deg (x^{b})$ and $\exists i$ $(1 \leq i \leq n)$ : $a_{n} = b_{n}, ..., a_{i + 1} = b_{i + 1}, a_{i} > b_{i}$ . (The right-most component of a―b is positive. )

Example 5.1 Compute ${(x + y + z + 1)}^{3}$ in $ℤ [x, y, z]$ . The monomials can be sorted by the different types of monomial order. (Here the degree of a monomial is given by this correspondence: $x^{a} = x^{a_{1}} y^{a_{2}} z^{a_{3}}$ .

The lexicographic order: $x > y > z$ ;

$x^{3} + 3 x^{2} y + 3 x^{2} z + 3 x^{2} + 3 x y^{2} + 6 x y z + 6 x y + 3 x z^{2} + 6 x z + 3 x + y^{3} + 3 y^{2} z + 3 y^{2} + 3 y z^{2} + 6 y z + 3 y + z^{3} + 3 z^{2} + 3 z + 1$

The reverse lexicographic order: z>y>x;

z³+3yz²+3x²+3z²+3y² z+6xyz+6yz+3x² z+6xz+3z+y³+3xy²+3y²+3x² y+6xy+3y+x³+3x²+3x+1

The degree reverse lexicographic order: $x > y > z$ ;

$\begin{array}{l} x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} + 3 x^{2} z + 6 x y z + 3 y^{2} z + 3 x z^{2} + 3 y z^{2} + z^{3} + 3 x^{2} + 6 x y + 3 y^{2} + 6 x z + 6 y z + 3 z^{2} \\ + 3 x + 3 y + 3 z + 1 \end{array}$

The difference between the lexicographic order and the reverse lexicographic order is apparent; it is simply a reversal. The difference between lexicographical order and the degree reverse is subtle; it could be understandable by these phrases by Ene and Herzog [9],

...in the lexicographic order, $u > v$

if and only if u has “more from the beginning” than v;

in the degree reverse lexicographic order, $u > v$

if and only if u has “less from the end” than v...

Let $f \neq 0$ be a polynomial in the ring $R = K [x_{1}, x_{2}, ..., x_{n}]$ with the monomial order $<$ . The ”initial monomial” ${in}_{<} (f)$ is the largest monomial included in $f$ (from which the coefficient is removed). The “initial coefficient” $l c (f)$ is the coefficient of ${in}_{<} (f)$ .Hence the “leading term” is given by the product of the initial coefficient and the initial monomial: $l c (f) {in}_{<} (f)$ . We use an extra definition: ${in}_{<} (0) = 0$ .

The initial ideal ${in}_{<} (I)$ is the monomial ideal, generated by the initial terms of the polynomials in $I$ ,

${in}_{<} (I) = {{in}_{<} (f) : f \in I}$

This ideal is a useful tool in the theory of Gröbner bases.

The Gröbner basis is defined now.

Definition 5.4 Let $I$ be the ideal in the polynomial ring $R$ , with the monomial order $<$ . The Gröbner basis is the sequence of elements $g_{1}, g_{2}, ..., g_{m}$ , such that ${in}_{<} (I) = ({in}_{<} (g_{1}), ..., {in}_{<} (g_{n})$ .

We could represent the polynomial $f$ by means of a sequence of polynomials $u_{1}, u_{2}, ..., u_{m} (\in I)$ in the following way (the standard expression)

$f = p_{1} u_{1} + p_{2} u_{2} + \dots p_{m} u_{m} + r$

such that

(i) No monomial in the remainder r is contained in the ideal $({in}_{<} (u_{1}), ... {in}_{<} (u_{n})$ ).
(ii) ${in}_{<} (f) \geq {in}_{<} (p_{i} u_{i}) f o r a l l i$

If $r = 0$ we say that f reduces to zero with respect to $u_{1}, u_{2}, ..., u_{m}$ . In general case, the standard expression is not unique. From this reason, we have to use Gröbner basis, since the standard expression by Gröbner basis is unique and any polynomial reduces uniquely by this basis. For example, consider the case with $f = x y - y^{2}$ , $g_{1} = x - y$ , and $g_{2} = x$ in the lexicographic order. There are two standard expression: $f = y g_{1}$ and $f = y g_{2} - y^{2}$ . However, the ideal $(g_{1}, g_{2})$ is generated by the Gröbner basis $(x, y)$ , by which f reduces to zero and it has the unique standard expression.

The Buchberger’s algorithm is the standard way to generate Gröbner basis [3,6,7,9,20-22]

Let us define the S-polynomial of two polynomials $f$ and $g$

$s p o l y (f, g) = \frac{l cm ({in}_{<} (f), {in}_{<} (g))}{c {in}_{<} (f)} f - \frac{l cm ({in}_{<} (f), {in}_{<} (g))}{d {in}_{<} (g)} g$

where $c$ and $d$ are the leading coefficients of $f$ and $g$ .

One can prove that

$g_{1}, ..., g_{m}$ are the Grb̈ner basis of ideal $I$ with respect to a monomial order $<$ ,

if and only if

$s p o l y (g_{i}, g_{j})$ reduces to zero with respect to $g_{1}, ..., g_{m}$ for $i < j$ .

The computational step is as follows.

Step–0 Let $G$ be the generating set of ideal $I$ .
Step–1 For every pair of polynomials $p, q$ in the ideal $G$ , compute $s p o l y (p, q)$ and its reminder $r$ with respect to $G$ .
Step–2 If all $s p o l y (p, q)$ reduce to zero with respect to $G$ , we have already obtained the Gröbner basis. If there are non-zero reminders $r \neq 0$ , add $r$ to $G$ and repeat again at Step–1.

The computation terminates after finite steps.

Let us see examples.

Example 5.2 Consider $f = x + y e$ and $g = y + x e$ in $R = ℝ [x, y, e]$ , with respect to lexicographic order $x > y > e$ . In the beginning, $G = {f, g}$ . As ${in}_{<} (f) = x$ and ${in}_{<} (g) = x e$ , $s p o l y (f, g) = e f - g = - y - y e^{2}$ . The leading monomial ${in}_{<} (s p o l y (f, g))$ is $y e^{2}$ . As the monomials in spoly(f,g) is not included by the monomial module ${(in}_{<} (f), {in}_{<} (g)) = (x, x e)$ , $s p o l y (f, g)$ does not reduce to zero; indeed it is the reminder itself. We add $h : = s p o l y (f, g)$ to $G$ so that $G = {f, g, h}$ . Then we compute more of s-polynomials : $s p o l y (h, g) = x y - y^{2} e = - y f$ and $s p o l y (h, f) = - x y - y^{2} e^{3} = - y f - y e h$ . Since $s p o l y (h, g)$ and $s p o l y (f, g)$ reduces to zero with respect to $G$ , we obtain the Gröbner basis $G$ . In fact, the initial term of $g = x e + y$ is divisible that of $f = x + e y$ , and $h = e f - g$ , $g$ is a redundant term which we can remove from the basis safely.

Example 5.3 Consider $f_{1} = x + e y$ , $f_{2} = y + e x$ $f_{3} = x^{2} + y^{2} - 1$ in $R = [x, y, e]$ , with respect to lexicographic orer $x > y > e$ . We have $G = {f_{1}, f_{2}, f_{3}}$ . We compute the s-polynomials: $s p o l y (f_{1}, f_{2}) = y e^{2} - y$ , $s p o l y (f_{1}, f_{3}) = x y e - y^{2} + 1$ , and $s p o l y (f_{2}, f_{3}) = x y - y^{2} e + e$ . These three polynomials reduce to $f_{4} = y e^{2} - y$ , f₅=-2y²+1, and $f_{6} = - 2 y^{2} e + e$ . We get $G = {f_{1}, f_{2}, f_{3}, f_{4}, f_{5}, f_{6}}$ and we compute the s-polynomials and the reminders. The only non-zero reminder is $(1 / 2) (e^{2} - 1)$ , to which $s p o l y (f_{4}, f_{5})$ and $s p o l y (f_{4}, f_{6})$ reduce. We have $G = {f_{1}, f_{2}, f_{3}, f_{4}, f_{5}, f_{6}, f_{7} = e^{2} - 1}$ . We compute the s-polynomials and ascertain that all of them reduce to zero. Thus $G = {x + e y, y + e x, x^{2} + y^{2} - 1, x y e - y^{2} + 1, - 2 y^{2} + 1, - 2 y^{2} e + e, e^{2} - 1}$ is the Gröbner basis. However, $y + e x$ , $x^{2} + y^{2} - 1$ , $x y e - y^{2} + 1$ and $- 2 y^{2} e + e$ are redundant: indeed they have the initial monomials divisible by those of other polynomials ( $\hat{G} = {x + e y, - 2 y^{2} + 1, e^{2} - 1}$ ) and reduce to zero with respect to $\hat{G}$ . Thus we can chose $\hat{G}$ as the Gröbner basis, and indeed this ideal satisfies the required property.

Example 5.4 Consider $I = (x + 1, 1)$ in $ℝ [x]$ . As $s p o l y (x + 1, x) = 1$ , The Gröbner basis is $(x + 1, x, 1) = {1}$ . This Gröbner basis is never to be zero, and the set of equation $x + 1 = 0 \land x = 0$ does not have any solution. In other words, the affine algebraic set of this ideal is empty $V (I) = V ({1}) = \emptyset$ . Likewise, in the more complicated case, by computing the Gröbner bases G, we can check the existence of the solutions of the set of polynomial equations.

In the above algorithm the generated Gröbner basis is not properly “reduced” by the terminology of several contexts. A reduced Gröbner basis $(g_{1}, ..., g_{n})$ should have the following property [23]:

The leading coefficient of each $g_{i}$ is 1.
for all $i \neq j$ , the monomials in $g_{j}$ are not divisible by ${in}_{<} (g_{i})$ .

The following statements are equivalent for a zero-dimensional ideal $I \subset S = K [x_{1}, x_{2}, ..., x_{n}]$ with a monomial order $<$ .

1. $I$ is a zero-dimensional ideal.

2. The affine algebraic set $V (I)$ is finite.

3. If $G$ is a Gröbner basis, then, for any $1 \leq i \leq$ n, there exists $g \in G$ such that ${in}_{<} (g) = x_{i}^{ν_{j}}$ for some $n u_{i} \geq 0$ .

4. $I$ is contained in finitely many maximal ideals of $S$ .

5. Let $Mon (A)$ be the set of monomials in $A$ . The set $Mon (S) \ Mon (i n_{<} (I))$ is a finite set.

6. $S / I$ is a $K$ -vector space of finite dimension.

The statement 3) enables us to detect a zero-dimensional ideal from its Gröbner basis, if the latter contains polynomials which have initial terms such that $x_{i}^{ν_{i}}$ for any $1 \leq i \leq n$ .

The feature of zero-dimensional ideal, given by statement 5) and 6), will be useful for solving polynomial equations by Stickelberger’s theorem, as is explained in section 5.12.

Example 5.5 For $I = (x^{2} + y^{2} + z^{2} - 1, x + y + z, x) \subset R [x, y, z]$ , the Gröbner basis with respect to lexicographic monomial order $x > y > z$ is $(2 z^{2} - 1, y + z, x)$ . This is the example of zero-dimensional ideals and it satisfies the statement 3).

Example 5.6 For $I = (x^{2} + y^{2} + z^{2} - 1, x + y + z) \subset ℝ [x, y, z]$ , the Gröbner basis with respect to lexicographic monomial order $x > y > z$ is $(2 y^{2} + 2 y z + 2 z^{2} - 1, x + y + z)$ . As the ideal depicts the intersection of the unit sphere and a plane surface, it is not zero-dimensional. Although the Gröbner basis has the terms $z^{2}$ and $z$ , these terms are not initial terms. Hence this ideal does not satisfy the statement 6).

Example 5.7 For $I = (x^{2} + y^{2} + z^{2} - 1, x + y + z, x) \subset R [x, y, z]$ , the Gröbner basis with respect to lexicographic monomial order $x > y > z$ is $(2 z^{2} - 1, y + z, x)$ . This is the example of zero-dimensional ideals and it satisfies the statement 3).

For a Gröbner basis ${f_{1}, f_{2}, ..., f_{m}}$ , there are relations as follows

$\sum_{i = 1}^{s} s_{i} f_{i} = 0$

by means of the set of polynomials ${s_{1}, s_{2}, ..., s_{m}}$ . (A trivial example is $f_{i} f_{j} - f_{j} f_{i} = 0$ .) Such a set of polynomials is a “module” (which is actually a vector space), and we call it the first Syzygy and denote it by $S y z (f_{1}, f_{2}, \dots, f_{n})$ . The basis set of this module is computed from the Gröbner basis.

When the computation of Gröbner basis is completed, there are relations among the generators of the basis of the form:

$s p o l y (f_{i}, f_{j}) = q_{i j, 1} f_{1} + q_{i j, 2} f_{2} + \dots + q_{i j, m} f_{m}$

Let us define

$r_{i j} = s p o l y (f_{i}, f_{j}) - q_{i j, 1} f_{1} - q_{i j, 2} f_{2} - \dots - q_{i j, m} f_{m}$

Then ${r_{i j}}$ generates $S y z (f_{1}, f_{2}, \dots, f_{n})$ . Moreover,even if $p_{1}, p_{2}, ..., p_{n}$ is not a Gröbner basis, we can compute $S y z (p_{1}, p_{2}, \dots, p_{n})$ through its Gröbner basis.

Example 5.8 Let us compute the syzygy of ${p_{1} = t x + e y, p_{2} = t x + e y, p_{3} = x^{2} + y^{2} - 1}$ with the lexicographic monomial order $t > x > y > e$ . $S y z (p_{1}, p_{2}, p_{3})$ are generated by three trivial generators $(- p_{3}, 0, p_{1}), (- p_{2}, p_{1}, 0), (0, - p_{3}, p_{1})$ , and by the non-trivial one, $(x^{2} y e + y^{3} e - y e, - x^{2} - y^{2} + 1, - y^{2} e^{2})$ .

Observe that the inner product of those generators and $(p_{1}, p_{2}, p_{3})$ is zero. The generators form a vector space.

Sygyzy is a module, in other words, a kind of vector space generated by the vectors, the entries of which are polynomials. We can compute the second syzygy in the vector generators of the first syzygy and, likewise, the higher syzygy, too. The successive computation of higher syzygy enables us to construct the “resolution” of a module M in a Noetherian ring; the computation terminates after a certain step so that we do not find any non-trivial sygyzy in the last step [23].

The reduction is a binary relation from one object to another, like an arrow going in one direction. We often call it the rewriting process.

Definition 5.5 A binary relation (denoted by the symbol $\to$ ) has the Church-Rosser property, if, whenever P and Q are connected by a path of arrows, P and Q have a common destination R by the relation.

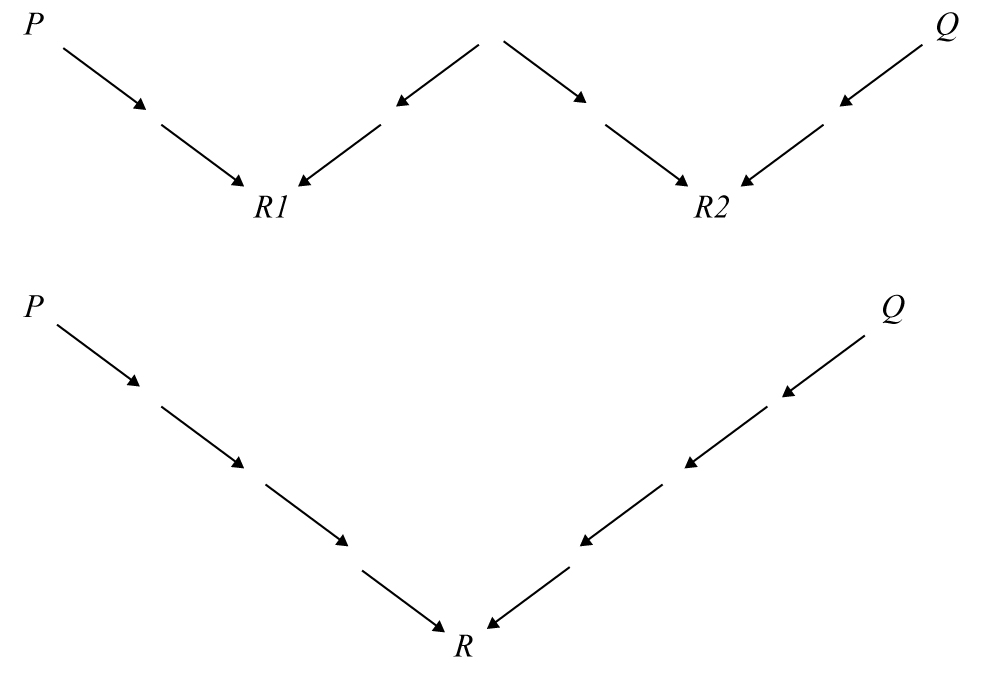
Hence we can define Gröbner bases in the other way: A basis is a Gröbner basis if and only if the reduction with respect to the bases has the Church-Rosser property, as is illustrated in Figure 3.

The original algorithm by Buchberger, as is presented here, is not so efficient. It produces a lot of useless pairs of polynomials $(p, q)$ , since such pairs give birth to s-polynomials $s p o l y (p, q)$ , which immediately reduce to zero or produce redundant polynomials. There are a lot of studies about the upper bound of the complexity of Gröbner bases, such as Hermann bound [24], Dube bound [25], Wiesinger’s theorem [26], and so on. Those bounds are determined by several factors: (1) the number of variables, (2) the number of polynomials in the ideal, (3) the number of possible s-polynomials, (4) the maximum degrees of the polynomials, etc. In the worst case, the complexity is doubly exponential in the number of variables [25,27-30]. However, the computation of the Gröbner basis is equivalent to the Gaussian elimination process of a large matrix (by the row reduction of Macauley matrix) [17,29,31,32]. For the case of homogeneous polynomial ideals, the complexity in the Gaussian elimination method is bounded by

$O (m D {(\begin{matrix} n + D - 1 \\ D \end{matrix})}^{ω})$

where $ω$ is a constant, m is the number of polynomials [33], $n$ is the dimension of the ring, and $D$ is the maximum degree of the polynomials [33]. In order to improve efficiency, one can employ more refined methods, such as Faugère’s $F_{4}$ and $F_{5}$ . Indeed the efficiency of $F_{5}$ [34, 35] outperforms the row reduction computation of Macaulay matrix [33].

In fact, the efficiency of the algorithm is highly dependent on the chosen monomial order. The lexicographic order is convenient for theoretical study, but it consumes a considerable quantity of computational resource. Thus one often has to compute the Gröbner basis by other monomial orders (say, the degree reversible lexicographic order) in order to facilitate the computation, and then, one can remake the computed result in lexicographic order, by means of FGLM (Faugère, Gianni, Lazard, Mora) algorithm [36].

There is another problem in the Gröbner bases generation. which is apparent in practice. The Buchberger’s algorithm applies the operation of addition, subtraction, multiplication, and division to the polynomial system. It often causes a great discrepancy in the degrees of the generated polynomials and the numerical scale of coefficients in the final result. In the computation presented in the introduction of this article, one can observe such a tendency. Thus, for the practical purpose, one must utilize several tricks to keep the polynomials as “slim” as one can [37-39].

Let us review what is the module. A $R -$ module M is an abelian group with scalar multiplication $R \times M \to M$ , such as $(a, m) \to a m \in M$ . It has the following property.

$1 m = m$
$(a b) m = a (b m)$
$(a + b) m = a m + b m$
$a (m + n) = a m + b m$

A free module is the module with a basis set ${e_{i}}$ . We can compute Gröbner bases of free modules. One of the purpose of this sort of computations is to study the linear equation of polynomials:

$(\begin{matrix} a_{11} & a_{12} & \dots & a_{1 n} \\ a_{21} & a_{22} & \dots & a_{2 n} \\ ⋮ & ⋮ \\ a_{n 1} & a_{n 2} & \dots & a_{n n} \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{matrix}) = (\begin{matrix} b_{1} \\ b_{2} \\ ⋮ \\ b_{n} \end{matrix})$

for which one might ask for the linear dependence of rows.

We define the monomial order in modules in these ways.

Position over coefficient : $u e_{i} > v e_{j}$ if $i < j$ or $i = j$ and $u > v$ .
(Example: $x_{2} e_{1} > x_{1} e_{2}$ ).
Coefficient over position $u e_{i} > v e_{j}$ : if $u > v$ or $v = v$ and $i < j$ . (Example: $x_{1} e_{2} > x_{2} e_{1}$ ).

In the similar way as in the case of polynomial, we chose the leading terms of the elements in a module; we also compute the s-polynomials and the reminders in order that we obtain the Gröbner basis. The slight difference is that when ${in}_{<} (f) = u e_{i}$ and ${in}_{<} (g) = v e_{i}$ we use the s-polynomial as follows:

$s p o l y (f, g) = \frac{l cm (u, v)}{l c (f) u} f - \frac{l cm (u, v)}{l c (g) u}$

(Here we use the notation $l c (x)$ to represent the coefficient of $i n_{<} (x)$ .)

Gröbner basis is a convenient tool to actually compute various mathematical objects in the commutative algebra.

Example 5.9 Elimination of variables: The intersection of ideal $I \subset R$ and the subring $S \subset R [x_{1}, x_{2}, ..., x_{n}]$ is computable. Let $G$ and let be a Gröbner basis of $I$ . Then $G_{t} = G \cap S$ is the Gröbner basis of $S$ . If we compute the Gröbner basis by means of lexicographic orders $x_{1} > x_{2} > ... > x_{n}$ , we obtain the set of polynomials,

${f_{1}^{i} (x_{n}), i = 1, ..., i_{1}}$ ,
${f_{2}^{i} (x_{n - 1}, x_{n}), i = 1, ..., i_{2}}$ ,
...
${f_{n - t + 1}^{i} (x_{t + 1}, ..., x_{n - 1}, x_{n}), i = 1, ... i_{n - t - 1}}$ ,
....
${f_{n}^{i} (x_{1}, x_{2}, ..., x_{n}), i = 1, ..., i_{n}}$ .

Thus we can easily get $G_{t} = G \cap S$ .

Example 5.10 Intersection of ideal $I$ and $J$ in $R$ . Let y be an extra variable. $I \cap J$ is computable by the relation $I \cap J = (I \cdot y \cdot R [y] + J \cdot (1 - y) \cdot R [y]) \cap R$ . The intersection of the right-hand side is computed by the elimination of variable $y$ .

Example 5.11 The ideal quotient I:J is computable. If $J = (f_{1}, ..., f_{s})$ , then $I : J = \cap_{j = 1}^{s} (I : f_{j})$ . In addition, for a single polynomial $f$ , $I \cap (f) = f \cdot (I : f)$ . We can compute $I \cap (f)$ and obtain the generators ${g_{1}, g_{2}, \dots, g_{m}}$ . Then $I : f$ is generated by ${g_{1} / f, g_{2} / f, ..., g_{m} / f}$ . Hence $I : J$ is computed as the intersection of $I : f_{j}$ .

Example 5.12 Saturation: it is defined for an ideal $I$ and a polynomial $f$ in a ring $S$ as follows.

$I : f^{\infty} = {g \in S : there exists i > 0 such that f^{i} g \in I}$

Let $t$ be a new variable, and let $\tilde{I}$ be the ideal generated in $S [t]$ by $I$ and by the polynomial $1 - f t$ . Then the saturation $I : f^{\infty} = \tilde{I} \cap S$ . [compsat]

Example 5.13 Radical membership: $f \in \sqrt{I} \Leftrightarrow f^{i} \in I$ for some $i > 0 \Leftrightarrow$ For all $g \in S$ , there exists $i (> 0)$ such that $f^{i} g \in I$ . $\Leftrightarrow I : f^{\infty} = S$ . Hence , if the ideal, $\hat{I}$ defined in example 5.12, has the Gröbner basis ${1}$ , then $f \in \sqrt{I}$ .

The Buchberger’s algorithm is actually the elimination in large matrices. It is the way of Faguère to do the row reduction in the large matrix. Let us see how it would work.

Consider the same problem: $f_{1} = x + y e$ , $f_{2} = y + x e$ , $f_{3} = x^{2} + y^{2} - 1$ . We compute the s-polynomials $e f_{1} - f 2$ and $x f_{1} - f_{3}$ . The coefficients in these polynomials are given in the matrix.

$(\begin{matrix} x f_{1} \\ e f_{1} \\ f_{2} \\ f_{3} \end{matrix}) = (\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & - 1 \end{matrix}) (\begin{matrix} x^{2} \\ x y e \\ x e \\ y e^{2} \\ y^{2} \\ y \\ 1 \end{matrix})$

The matrix in the right hand side is the so-called Macaulay matrix of the second order. The row reduction yields:

$(\begin{matrix} x f_{1} \\ e f_{1} \\ f_{4} \\ f_{5} \end{matrix}) = (\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1 & 0 & 1 & 0 \\ 0 & - 1 & 0 & 0 & 1 & 0 & - 1 \end{matrix}) (\begin{matrix} x^{2} \\ x y e \\ x e \\ y e^{2} \\ y^{2} \\ y \\ 1 \end{matrix})$

We obtain $f_{4} = - y e^{2} + y$ and $f_{5} = - x y e + y^{2} - 1$ and now we have the temporary Gröber basis $G = {f_{1}, f_{4}, f_{5}}$ ; $f_{2}$ and $f_{3}$ can be excluded in the consideration, because they are “top-reducible” by $f_{1}$ and easily recovered by the present $G$ .

Let us compose the third order Macaulay matrix:

$(\begin{matrix} y e f_{1} \\ f_{5} \end{matrix}) = (\begin{matrix} 1 & 1 & 0 & 0 \\ - 1 & 0 & 1 & - 1 \end{matrix}) (\begin{matrix} x y e \\ y^{2} e^{2} \\ y^{2} \\ 1 \end{matrix})$

The row reduction yields this:

$(\begin{matrix} y e f_{1} \\ f_{6} \end{matrix}) = (\begin{matrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & - 1 \end{matrix}) (\begin{matrix} x y e \\ y^{2} e^{2} \\ y^{2} \\ 1 \end{matrix})$

We obtain $f_{6} = y^{2} e^{2} + y^{2} - 1$ . Now $G = {f_{1}, f_{4}, f_{6}}$

We again compute the third order Macaulay matrix

$(\begin{matrix} y f_{4} \\ f_{6} \end{matrix}) = (\begin{matrix} - 1 & 1 & 0 \\ 1 & 1 & - 1 \end{matrix}) (\begin{matrix} y^{2} e^{2} \\ y^{2} \\ 1 \end{matrix})$

The row reduction yields:

$(\begin{matrix} y f_{4} \\ f_{7} \end{matrix}) = (\begin{matrix} - 1 & 1 & 0 \\ 0 & 2 & - 1 \end{matrix}) (\begin{matrix} y^{2} e^{2} \\ y^{2} \\ 1 \end{matrix})$

We obtain $f_{7} = 2 y^{2} - 1$ . Now $G = {f_{1}, f_{4}, f_{7}}$ .

We compute the fourth order Macaulay matrix:

$(\begin{matrix} y f_{4} \\ \frac{1}{2} e^{2} f_{7} \end{matrix}) = (\begin{matrix} - 1 & 1 & 0 & 0 \\ 1 & 0 & - 1 / 2 & 0 \end{matrix}) (\begin{matrix} y^{2} e^{2} \\ y^{2} \\ e^{2} \\ 1 \end{matrix})$

We do the row reduction in the fourth order Macaulay matrix:

$(\begin{matrix} y f_{4} \\ \frac{1}{2} f_{8} \end{matrix}) = (\begin{matrix} - 1 & 1 & 0 & 0 \\ 0 & 1 & - 1 / 2 & 0 \end{matrix}) (\begin{matrix} y^{2} e^{2} \\ y^{2} \\ e^{2} \\ 1 \end{matrix})$

We obtain $f_{8} = 2 y^{2} - e^{2}$ . Now $G = {f_{1}, f_{4}, f_{7}, f_{8}}$ . However, as $f_{7} - f_{8}$ yields $f_{9} = e^{2} - 1$ , and as $f_{4} = - y^{2} f_{9}$ , would be ${f_{1}, f_{7}, f_{9}} = {x + y e, 2 y^{2} - 1, e^{2} - 1}$ . The s-polynomials for $G$ are computed now:

$s p o l y (f_{1}, f_{7}) = \frac{1}{2} x + y^{3} e = \frac{1}{2} f_{1} + \frac{y e}{2} f_{7}$

$s p o l y (f_{1}, f_{9}) = x + y e^{3} = f_{1} + y e f_{9}$ ,

$s p o l y (f_{7}, f_{9}) = 2 y^{2} - e^{2} = f_{7} - f_{9}$ .

As those s-polynomials reduce to zero with respect to $G$ , it is proved that $G$ is a Gröbner basis.

In the above example, we process the computation carefully so that the unnecessary polynomials are removed immediately as soon as they appear; we also limit the computation in the Macaulay matrices which would be as small as possible, although these matrices might be embedded into a very large one. Indeed we have done the row reduction numerically, not symbolically, in a very large, but sparse matrix. The algorithms $F_{4}$ and $F_{5}$ by Faugère adopt these policies in a systematical way so that these algorithms are of the most efficient methods to generate Gröbner bases.

In [2], an alternative of the numerical solution, instead of Gröbner basis, is also used. This method is based on Stickelberger’s theorem. In general, for a zero-dimensional ideal $I \subset R = k [x_{1}, ... x_{n}]$ , $R / I$ is a $k$ -vector space of finite dimension; that is to say, the vector space is spanned by the set of monomials and the result of the multiplication between two monomial is also represented by the linear combination of the monomial basis. Therefore, according to the assertion of the theorem, the operation of a monomial to the monomial basis is thought to be the operation of a matrix in . And the eigenvalue of the matrix gives the numeral value of the corresponding monomial at $V (I)$ .

Consider $I = (x + y e, y + x e, x^{2} + y^{2} - 1) \subset R = ℝ [x, y]$ . As a Gröbner basis of $I$ is $(x + y e, 2 y^{2} - 1, e^{2} - 1)$ , the monomial basis in $R / I$ is given by ${1, \bar{y} \bar{e}, \bar{e}, \bar{y}}$ , from which $x$ is dropped. The transformation by and are given as follows.

$\begin{array}{r} \bar{y} (\begin{matrix} \bar{1} \\ \bar{y} \bar{e} \\ \bar{e} \\ \bar{y} \end{matrix}) & = & (\begin{matrix} \bar{y} \\ {\bar{y}}^{2} \bar{e} \\ \bar{y e} \\ {\bar{y}}^{2} \end{matrix}) \\ = & (\begin{matrix} \bar{y} \\ 1 / 2 \bar{e} \\ \bar{y} \bar{e} \\ 1 / 2 \end{matrix}) \\ = & (\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 / 2 & 0 \\ 0 & 1 & 0 & 0 \\ 1 / 2 & 0 & 0 & 0 \end{matrix}) (\begin{matrix} \bar{1} \\ \bar{y} \bar{e} \\ \bar{e} \\ \bar{y} \end{matrix}) . \end{array}$

$\begin{array}{r} \bar{e} (\begin{matrix} \bar{1} \\ \bar{y} \bar{e} \\ \bar{e} \\ \bar{y} \end{matrix}) & = & (\begin{matrix} \bar{e} \\ \bar{y} {\bar{e}}^{2} \\ {\bar{e}}^{2} \\ \bar{y} \bar{e} \end{matrix}) \\ = & (\begin{matrix} \bar{e} \\ \bar{y} \\ 1 \\ \bar{y} \bar{e} \end{matrix}) \\ = & (\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}) (\begin{matrix} \bar{1} \\ \bar{y} \bar{e} \\ \bar{e} \\ \bar{y} \end{matrix}) . \end{array}$

The transformation matrices $M_{y}$ (by $y$ ) and $M_{e}$ (by $e$ ) are those in the right hand side in the both equations. It is easily checked that there are four eigenvectors, common both for $M_{y}$ and $M_{e}$ , which lie in $R / I$ :

$(\begin{matrix} \bar{1} \\ \bar{y} \bar{e} \\ \bar{e} \\ \bar{y} \end{matrix}) = (\begin{matrix} 1 \\ 1 / \sqrt{2} \\ 1 \\ 1 / \sqrt{2} \end{matrix}), (\begin{matrix} 1 \\ - 1 / \sqrt{2} \\ 1 \\ - 1 / \sqrt{2} \end{matrix}), (\begin{matrix} 1 \\ 1 / \sqrt{2} \\ - 1 \\ - 1 / \sqrt{2} \end{matrix}) (\begin{matrix} 1 \\ - 1 / \sqrt{2} \\ - 1 \\ 1 / \sqrt{2} \end{matrix})$

Now we have obtained the numeral values of $e$ and $y$ at $V (I)$ from $\bar{e}$ and $\bar{y}$ . In fact, the eigenvalues $M_{y}$ and $M_{e}$ also give us the value of $y$ and $e$ at $V (I)$ . As for the value of $x$ , we easily compute it from the polynomial relation by the ideal $I$ .

As we have seen, the zero-dimensional ideal is detected immediately after the computation of its Gröbner ideal. However, it takes a little of algebra to compute the non-zero dimension of an ideal [40].

Let $I \subset R [x_{1}, ..., x_{n}]$ be an ideal. Then the Krull dimension of $R [x_{1}, ..., x_{n}] / I$ is given by an integer $d$ , i.e., ${dim}_{K} (R [x_{1}, ..., x_{n}] / I) = d$ , such that d is the maximal cardinality of a subset of variables $u \subset {x_{1}, ..., x_{n}}$ with $I \cap R [u] = (0)$ . (A maximal independent set of variables with respect to $I$ is a subset $u$ of variables of maximal cardinality, defined as this.)
Let $>$ be any monomial ordering on $R [x_{1}, ..., x_{n}]$ . And let $I \subset R [x_{1}, ..., x_{n}]$ be an ideal. Then the Krull dimension of the quotient ideal is computed by means of the initial ideal ${in}_{<} (I)$ of $I$ :

${dim}_{K} (R [x_{1}, ..., x_{n}] / I) = {dim}_{K} (R [x_{1}, ..., x_{n}] / {in}_{<} (I))$

Hence we only have to consider the initial ideal ${in}_{<} (I)$ , instead of the ideal $I$ itself.

Let $I = (m_{1}, ..., m_{k}) \subset R [x_{1}, ..., x_{n}]$ be an ideal with monomial generators $m_{i}$ . Let denote ${x_{1}, ..., x_{n}}$ by $X$ . Define $d (I, R [x])$ in a recursive way $d ((0), R [X]) = n$ , and
$d (I, R [X]) = max {d (I |_{x_{i} = 0}, R [X \ x_{i}]) for x_{i} such that x_{i} | m_{1}}$ .
Then $d (I, K [x]) = {dim}_{K} (R [x] / I)$ .

Example 5.14 Consider $I = (x y) \subset ℝ [x, y]$ .

$d (I, ℝ [x, y]) = max {d ((0), ℝ [x]), d ((0), ℝ [y])}$ , as $I |_{x = 0} = I |_{y = 0} = (0)$ . Since $d ((0), ℝ [x]) = d ((0), ℝ [y]) = 1$ , $d (I, ℝ [x, y]) = {dim}_{K} ℝ [x, y] / (x y) = 1$ .

Example 5.15 Consider $I = (x y - 1) \subset ℝ [x, y]$ . Then we have to consider ${in}_{<} (I) = (x y)$ and the conclusion is the same as the previous example.

Example 5.16 Consider $I = (x + e y, y + e x) \subset ℝ [x, y, e]$ with lexicographic order $x > y > e$ . The Gröbner basis is ${y - y e^{2}, x + e y}$ . Hence ${in}_{<} (I) = (y, x)$ . Since $u = {e}$ is the set of variable of maximal cardinality with $(y, x) \cap ℝ [e] = (0)$ we have ${dim}_{K} ℝ [x, y, e] / I = 1$ . (We can arrive at the same conclusion by means of the recursive function $d (I, ℝ [x, y, e]) .)$ .)

In the example of the hydrogen molecule in section 3, we have seen that the polynomial secular equation is made into the triangular form, in which the relation of variables is clarified, almost to represent the roots themselves. The mathematical foundation of such computations is the primary ideal decomposition.

There are two special sorts of ideal: prime ideal and primary ideal, as we have seen in the previous section. One can comprehend these sorts of ideal with the analogy of elementary number theory. An integer is decomposed as $n = p_{1}^{a_{1}} p_{2}^{a_{2}} \dots p_{n}^{a_{n}}$ by the prime factorization. The ideal of the integer n is $n ℤ$ (the integer multiple of $n$ ); and it is represented by $n ℤ = p_{1}^{a_{1}} ℤ \cap p_{2}^{a_{2}} ℤ \cap \dots \cap p_{n}^{a_{n}} ℤ$ as the intersection of the ideals generated by certain powers of primes.

An ideal in the commutative algebra, likewise, could be decomposed as the intersection of primary ideals [3]: $I = \underset{i}{\cap} p_{i}$

One of the most elementary procedure for primary ideal decomposition is summarized as follows [41]. Let $I$ be the ideal in a Noetherian ring $R$ , and $r, s \in R$ are elements such that $r \notin \sqrt{I}$ , $s \notin I$ and $r s \in I$ .

1. Find $n$ such that $I : r^{\infty} = I : r^{n}$ .

2. Let $I_{1} = I + (r^{n})$ and $I_{2} = I : (r^{n})$ .

3. The ideal $I_{1}$ and $I_{2}$ are larger than $I$ . The decomposition process must be done for each of them. By choosing some proper $r$ , we can decompose $I_{1}$ and $I_{2}$ , hence $I$ by primary ideals.

Example 6.1 Consider $J = (x + e y, y + e x)$ in $R = [x, y, e]$ with the lexicographic order $x > y > e$ .

$y$ is not in the radical $\sqrt{J}$ ; and $y \cdot (e^{2} - 1) = e y (x + e y) - y (y + e x) \in J$ . Thus we set $r = y$ and $s = e^{2} - 1$
Let $J_{1} \equiv (J, y) = (y, x + y e, y + x e)$ . This is a primary (in fact, a prime) ideal, and $J : y = J : y^{2} = ...$ (stabilized).
Let $J_{2} \equiv J : y = (e^{2} - 1, x + y e)$ : this is because of another representation $J = (y (e^{2} - 1), x + y e)$ . The ideal $J_{2}$ can be decomposed again.
• Now take $r = e - 1$ , $s = e + 1$ .
$J_{21} \equiv (J_{2}, e - 1) = (e - 1, x + e y) = (e - 1, x + y)$ . This ideal is primary (in fact, prime).
$J_{22} \equiv (J_{2} : e - 1) = (e + 1, x - y)$ and $J_{2} : (e - 1) = J_{2} : {(e - 1)}^{2} = ...$ (stabilized). This ideal is primary (in fact, prime).

Now we have done the primary ideal decomposition: $J = J_{1} \cap J_{21} \cap J_{22}$ .

We should notice that the ideal is the secular equation of the diatomic system,
$(\begin{matrix} 0 & - 1 \\ - 1 & 0 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = e (\begin{matrix} x \\ y \end{matrix})$

The primary ideal decomposition is the operation equivalent to the eigenstate computation by means of linear algebra: the solutions of the secular equation are given by the affine algebraic sets of the computed ideals. We obtain the eigenvalue $e = 1$ and $e = - 1$ for which the eigenvectors are $(x, x)$ and $(x, - x)$ .

In fact, the above example is one of the simplest cases which we can compute manually. The general algorithm for ideal decomposition is first proposed by Eisenbud [42]; and practical algorithms are developed by Gianni, Trager and Zacharias [43], by Shimoyama and Yokoyama [44], by Möller [45] and by Lazard . (As for the semi-algebraic set, one can do similar decomposition, as is studied by Chen and Davenport [46].) The comparison of algorithms is given in [10].

In this section, we review the primary ideal decomposition algorithm of Gianni, Trager, and Zacharias (GTZ algorithm) [18, 40]. In the algorithm which we have seen in the previous section, we have to search a “key polynomial” by trial and error to decompose an ideal. In contrast, GTZ algorithm enables us to find such a key in a more rational way.

A maximal ideal $I_{M} \subset K [x_{1}, ..., x_{n}]$ is called in general position with respect to the lexicographical ordering $>$ with $x_{1} > ... > x_{n}$ , if there exist $g_{1}, ..., g_{n} \in K [x_{n}]$ such that $I_{M} = (x_{1} + g_{1} (x_{n}), ..., x_{n - 1} + g_{n - 1} (x_{n}), g_{n} (x_{n}))$ .
When an ideal is decomposed by primary ideal decomposition $I = Q_{1} \cap \dots \cap Q_{s}$ , the prime ideals $P_{i} = \sqrt{Q_{i}}$ are called associated primes of $I$ . $P_{i}$ is a minimal associated prime of $I$ if $P_{i} \neq P_{j}$ for all $j \neq i$ .
A zero-dimensional ideal $I \in K [x_{1}, ..., x_{n}]$ is called in general position with respect to the monomial order $>$ with $x_{1} > \dots x_{n}$ ), if all associated primes $P_{1}, ..., P_{s}$ are in general position and $P_{i} \cap K [x_{n}] \neq P_{j} \cap K [x_{n}]$ for $i \neq j$ .

Theorem 6.1 (Zero-dimensional Decomposition) Let $I \in K [x_{1}, ..., x_{n}]$ be a zero-dimensional ideal. Let $(f) = I \cap K [x_{n}]$ , $f = f_{1}^{ν_{1}} \dots f_{s}^{ν_{s}}$ with $f_{i} \neq f_{j}$ for $i \neq j$ . Then the decomposition of ideal $I$ is given by $I = \cap_{i = 1}^{s} (I, f_{i}^{v_{i}})$ .

If I is in general position with respect to the monomial order $>$ with $x_{1} > ... > x_{n}$ , then $(I, f^{ν_{i}})$ are primary ideals for all $i$ .

Theorem 6.2 (Ideal decomposition in general case) Let $X = (x_{1}, ..., x_{n})$ . Let $I ⊊ K [X]$ be an ideal, and let $u \subset X$ be a maximal independent set of variables for . Then these statements hold.

(i) The ideal $I K (u) [X \ u$ ] generated by $I$ in $K (u) [x \ u]$ is zero-dimensional. We denote the field of rational functions on $K$ with variables u by $K (u)$ .

(ii) Let ${g_{1}, ... g_{s}} \subset I$ be a Gröbner basis of $I K (u) [x \ u]$ . Let $h = lcm (lc (g_{1}), ..., lc (g_{s})) \in K [u]$ . Then $I K (u) [x \ u] \cap^{} K [x] = I : h^{\infty}$ . If $I : h^{d} = I : h^{d + 1}$ , then $I = (I : h^{d}) \cap (I, h^{d})$ .

(iii) If $I K (u) [X \ u]$ = $Q_{1} \cap \dots \cap Q_{s}$ is an irredundant primary decomposition, then $I K (u) [x \ u] \cap^{} K [X]$ $= (Q_{1} \cap K [X]) \cap ... \cap (Q_{s} \cap K [X])$ is also an irredundant primary decomposition.

Example 6.2 Consider $I = x + e y, y + e x$ in $ℚ [x, y, e]$ with lexicographic order $x > y > e$ . We know a Gröbner basis of I is ${y (e^{2} - 1), x + e y}$ .

Choose $u = {y}$ as a maximal independent set of variables.
$I ℚ (y) [x, e] = (e^{2} - 1, x + e y)$ . This ideal is a Gröbner basis in $ℚ (y) [x, e]$ .
Then $h = lcm (lc (e^{2} - 1), lc (x + e y)) = x e^{2}$ .
$J : = I : h = I : h^{2} = {(e^{2} - 1, x + e y)}_{ℚ [x, y, e]}$ . And $(I, h) = (x + e y, y + e x, x e^{2}) = (x, y)$ . We have a decomposition $I = (I : h) \cap (I, h)$ .
We decompose $J$ . As is zero-dimensional in $ℚ (y) [x, e]$ , we apply the algorithm in zero-dimensional case. Since $e^{2} - 1 = (e + 1) (e - 1)$ , the decomposition of $J$ is given by $J = (J, (e + 1)) \cap^{} (J, (e - 1)) = (e + 1, x - y) \cap^{} (e - 1, x + y)$ . As the ideal $J$ is in general position with respect to lexicographic order $x > e$ in $ℚ (y) [x, e]$ , $(J, (e + 1))$ and $(J, (e - 1))$ are primary ideals. Notice that we are working in $ℚ (y) [x, e]$ . However, as the decomposition of $J ℚ [x, y, e]$ inherits that of $J ℚ (y) [x, e]$ , we have obtained the required decomposition.

In case of the systems of polynomial equations ${p_{i} (x_{1}, x_{2}, ... x_{n}) | i = 1... m}$ which have only finitely many solutions (i.e. to be zero-dimensional), several methods methods are proposed [45,47] which decompose the solution set into finitely many subset of the triangular form with respect to the variables entries,

${f_{1}^{l} (x_{1}), f_{1}^{l} (x_{1}, x_{2}), ..., f_{n}^{l} (x_{1}, x_{2}, ... x_{n}) | l = 1, ... L}$

This kind of algorithm is used in the application of algebraic geometry in molecular orbital theory as is demonstrated in section 3, instead of conventional linear algebra.

Let us review the triangular decomposition algorithm by Möller [45]. The algorithm is based upon several lemmas.

Lemma 6.1 (Lemma 2 in [45]) Let A be an ideal in a ring $R = K [x_{1}, ..., x_{n}]$ such that Krull dimension of the residue class ring $R / A$ is zero : $d i m (R / A) = 0$ . If $B$ is an ideal such that $B \subset A$ and if $m \in ℕ$ is sufficiently large, the affine algebraic set $V (A)$ is the disjoint union: $V (A) = V (A : B^{m}) \cup V (B)$ with

$V (B) = {y \in V (A) | \forall b \in B : b (y) = 0}$

$V (A : B^{m}) = {y \in V (A) | \exists b \in B : b (y) \neq 0}$ .

(The definition of $V (B)$ of this theorem, given in [45], is slightly different from the conventional one. In this section only, we use this definition.)

Lemma 6.2 (Lemma 3 in [45]) Let A is a ideal in a ring $R$ such that Krull-dimension of $R / A$ equals to zero $\dim k (R / A) = 0$ and let $B$ be another ideal in $R$ such that $A \subseteq B = (g_{1}, ..., g_{s})$ . Then, for sufficiently large $m, m_{1}, ..., m_{s} \in ℕ$

$V (A : B^{m}) = \cup_{i = 1}^{s} V ((A + (g_{1}, ..., g_{i - 1}) : g_{i}^{m_{i}})$

with $V ((A + (g_{1}, ..., g_{i - 1}) : g_{i}^{m_{i}}) = {y \in V (A) | g_{1} (y) = ... = g_{i - 1} (y) = 0 \neq g_{i} (y)}$ . In addition, if A is a radical ( $A = \sqrt{A}$ ), the above relation holds for all positive $m, m_{1}, ..., m_{s}$ .

Lemma 6.3 (Lemma 5 iii) in [45]). Let $f_{i} : = \sum_{j = 0}^{d_{i}} {\tilde{g}}_{i j} (x_{1}, ..., x_{n - 1}) x_{n}^{d_{i} - j}$ with nonzero polynomials ${\tilde{g}}_{i j}$ , $i = 1, ..., r$ .

If $F : = {f_{1}, ..., f_{r}}$ is a Gröbner basis with respect to a monomial order <, then $G = {{\tilde{g}}_{10}, ... {\tilde{g}}_{r 0}}$ is a a Gröbner basis with respect to $<$ .

Lemma 6.4 (Lemma 7 in [45]). Let $G : = {f_{1}, ..., f_{r}}$ be a reduced Gröbner basis with respect to a monomial order $<$ , where $x_{n}$ is lexicographically in front of ${x_{1}, .., x_{n - 1}}$ , and let

${x_{1 f_{i} : = \sum_{j = 0}^{d_{i}} {\tilde{g}}_{i j} (x_{1}, ..., x_{n - 1}) x_{n}^{d_{i} - j}}, .., x_{n - 1}}$

with nonzero polynomials ${\tilde{g}}_{i j}$ , $i = 1, ..., r$ , and $l t (f_{r}) < \dots < l t (f_{1})$ . If $g_{10}$ is a constant, then the ideal quotient $(f_{2}, ..., f_{r}) : f_{1}$ has the Gröbner basis (with respect to $<$ ) ${{\tilde{g}}_{2}, ..., {\tilde{g}}_{r 0}}$ and $f_{1} \notin (f_{2}, ... f_{r})}$ . Indeed, if ${f_{1}, ..., f_{r}}$ generates a zero-dimensional ideal, ${\tilde{g}}_{10}$ is constant by Lemma 6 in [45].

The algorithm is summarized as follows:

Let $A (\subset R [x_{1}, ..., x_{n}]$ ) be a zero-dimensional ideal with a reduced Gröbner basis ${f_{1}, ..., f_{r}}$ with respect to a monomial order <. Let B: $= (f_{2}, ..., f_{r}) : f_{1} + (f_{1})$ . Then V(A) is the union as V(A)=V(A:B^m)∪V(B). (It is easily checked that for ideals I,J, the relation V(I∩J)=V(I)∪V(J) holds. Hence the decomposition of the affine algebraic set is equivalent to that of ideal: $K = I \cap J$ .) The varieties involved in the union have following properties.

For $V (B)$ (which is one of the components of the decomposition), it holds that $V (B) = V (f_{1}) \cap^{} V ({\tilde{f}}_{2}, ..., {\tilde{f}}_{r})$ and ${{\tilde{f}}_{2}, ..., {\tilde{f}}_{r}}$ is a reduced Gröbner basis.
By lemma 4.4, $V (A : B^{m})$ is the disjoint union of the zero-zets,
$V (A : f_{1}^{m_{1}}), V ((A + (f_{1})) : {\tilde{f}}_{2}^{m_{2}}), ..., V ((A + (f_{1}, {\tilde{f}}_{2}, ..., {\tilde{f}}_{r - 1})) : {\tilde{f}}_{r}^{m_{r}})$
These sets are other components of the decomposition of $V (A)$ .
$V (A : (f_{1})^{m}) = \emptyset$ (because $f_{1} \in A$ ): this item is removed.
The Gröbner bases are computable for the ideals $A + (f_{1}) : {\tilde{f}}_{2}^{m_{2}}$ , ... , $A + (f_{1}, {\tilde{f}}_{2}$ , ..., ${\tilde{f}}_{r - 1})) : {\tilde{f}}_{r}^{m_{r}}$ . These Gröbner bases are in $R [x_{1}, ..., x_{n - 1}]$ (where the dimension is exactly dropped by one). Therefore we go down into $R [x_{1}, ..., x_{n - 1}]$ and in this ring we have the set of ideals which are to be processed again.
Iteratively we apply the algorithm to the set of ideals and drop the variable one by one; the process shall terminate after finite steps.

Let us consider the problem

$f_{1} = x + y^{2} e, f_{2} = y + x^{2} e, f_{3} = x^{2} + y^{2} - 1$

The reduced Gröbner basis with respect to the lexicographic order $x > y > e$ is given by

$p_{1} = x + y + e, p_{2} = 2 y^{2} + 2 y e + e^{2} - 1, p_{3} = 2 y e^{2} + 2 y + e^{3} + e, p_{4} = e^{4} - e^{2} - 2$

We apply the triangulation to $A_{0} = (p_{1}, p_{2}, p_{3}, p_{4})$ . For variable , it exists only in $p_{1}$ . Thus $p_{1}$ should be added in all components of the decomposition. We only decompose the smaller system $A = (p_{2}, p_{3}, p_{4})$ . For the variable $y$ , ${\tilde{p}}_{3} = 2 e^{2} + 2$ , ${\tilde{p}}_{4} = e^{4} - e^{2} - 2$ . By the removal of the redundant term, the simpler Gröbner basis for $({\tilde{p}}_{3}, {\tilde{p}}_{4})$ is, which is also a Gröbner basis of $(p_{3}, p_{4}) : p_{2}$ .

As for the decomposition $V (A) = V (B) \cap V (A : (e^{2} + 1)^{m})$ , the components are given as

$B = (p_{3}, p_{4}) : p_{2} + (p_{2}) = (e^{2} + 1, 2 y^{2} + 2 y e + e^{2} - 1) = (e^{2} + 1, y^{2} + y e - 1)$

$A : (e^{2} + 1) = (e^{2} - 2, 2 y + e)$

Indeed, the last statement implies the saturation: since, for $m = 1, 2, ...$ ,

$A : {(e^{2} + 1)}^{m} = (e^{2} - 2, 2 y + e)$

Thus we obtain the decomposition of $(f_{1}, f_{2}, f_{3}, f_{4})$ as the intersection of $(e^{2} + 1, y^{2} + y e + 1, p_{1})$ and $(e^{2} - 2, 2 y + e, p_{1})$ .

Let us execute molecular orbital computation by means of algebraic geometry. The example is a hexagonal molecule, like benzene, where s-orbital is located at each atom and interacts only with the nearest neighbors. as is depicted in Figure 4.

The secular equation for a hexagonal molecule, like a benzene, could be given by the simplest model:

$(\begin{matrix} 0 & T & 0 & 0 & 0 & T \\ T & 0 & T & 0 & 0 & 0 \\ 0 & T & 0 & T & 0 & 0 \\ 0 & 0 & T & 0 & T & 0 \\ 0 & 0 & 0 & T & 0 & T \\ T & 0 & 0 & 0 & T & 0 \end{matrix}) (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \\ c_{4} \\ c_{5} \\ c_{6} \end{matrix}) = ε (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \\ c_{4} \\ c_{5} \\ c_{6} \end{matrix})$

We place one orbital in each of the vertex of the hexagon; we assume the interaction between the nearest neighbors with the hopping parameter $T$ ; the wavefunction is given by the coefficients $(c_{1}, ..., c_{6})$ to six atomic orbitals. (We assume the following model: $| ψ 〉 = \sum_{i = 1}^{6} C_{i} | a_{i} 〉$ such that $〈 a_{i} | a_{j} 〉 = δ_{i, j}$ ; and $H = \sum_{i = 1}^{6} | a_{i} 〉 T 〈 a_{i + 1} |$ in the hexagonal closed graph with $a_{7} = a_{1}$ .)

The corresponding energy functional is given by

$\begin{array}{l} U = T c_{2} (c_{1} + c_{3}) + T c_{3} (c_{2} + c_{4})+ T c_{4} (c_{3} + c_{5}) \\ + T c_{5} (c_{4} + c_{6}) + T_{6} (c_{5} + c_{1}) + T c_{1} (c_{6} + c_{2}) \\ - e (c_{1}^{2} + c_{2}^{2} + c_{3}^{2} + c_{4}^{2} + c_{5}^{2} + c_{6}^{2} -1) \end{array}$

The ideal from the secular equation is represented as:

I=(-2*c1*e+2*c2*T+2*c6*T,
2*c1*T-2*c2*e+2*c3*T,
2*c2*T-2*c3*e+2*c4*T,
2*c3*T-2*c4*e+2*c5*T,
2*c4*T-2*c5*e+2*c6*T,
2*c1*T+2*c5*T-2*c6*e,
-c1^2-c2^2-c3^2-c4^2-c5^2-c6^2+1).

We assume that

$I \subset ℚ [c_{1}, c_{2}, c_{3}, c_{4}, c_{5}, c_{6}, T, e, U]$

with the lexicographic monomial order

$c_{1} > c_{2} > c_{3} > c_{4} > c_{5} > c_{6} > T > e > U$

The Gröbner basis is given in Table 2:

The first entry of the list in Table 2 shows the relation between the energy e and the hopping integral T. Then the polynomials including other variables (c₆,c₅,....,c₁) appear in succession. This is the example of variable elimination.

Let us evaluate the energy functional U. For this purpose, we make a new ideal $I + (f)$ with a polynomial $f$ which equates the variable U and the definition of the energy functional at $f = 0$ :

$\begin{array}{l} f = T c_{2} (c_{1} + c_{3}) + T c_{3} (c_{2} + c_{4}) c_{3} + T c_{4} (c_{3} + c_{5}) \\ + T c_{5} (c_{4} + c_{6}) + T_{6} (c_{5} + c_{1}) + T c_{1} (c_{6} + c_{2}) \\ - e (c_{1}^{2} + c_{2}^{2} + c_{3}^{2} + c_{4}^{2} + c_{5}^{2} + c_{6}^{2} -1)- U \end{array}$

The Gröbner basis of the ideal $I + (f)$ is given in Table 3. The first polynomial gives the relation between the total energy U and the hopping integral, while the other variables are swept into remaining polynomials. Consequently, it follows that, by means of symbolic computation, we have executed the molecular orbital computation and have obtained the
Table 2: Gröbner basis of the secular equation of the hexagonal molecule. _[1]=e^4-5*e^2*T^2+4*T^4
_[2]=6*c6^2*e^2-6*c6^2*T^2-e^2+T^2
_[3]=2*c5*e^2*T-2*c5*T^3-c6*e^3+c6*e*T^2
_[4]=c5*e^3-c5*e*T^2-2*c6*e^2*T+2*c6*T^3
_[5]=4*c5^2*T^2-4*c5*c6*e*T-4*c6^2*e^2
+8*c6^2*T^2+e^2-2*T^2
_[6]=4*c5^2*e-4*c5*c6*T+4*c6^2*e-e
_[7]=24*c5^2*c6^2*T-4*c5^2*T-24*c5*c6^3*e
+4*c5*c6*e+24*c6^4*T-10*c6^2*T+T
_[8]=24*c5^4*T-16*c5^3*c6*e+16*c5^2*c6^2*T
-10*c5^2*T+8*c5*c6^3*e+2*c5*c6*e-4*c6^2*T+T
_[9]=c4*T-c5*e+c6*T
_[10]=c4*e+12*c5^3*T-8*c5^2*c6*e+8*c5*c6^2*T
-4*c5*T+4*c6^3*e
_[11]=c3*T-c4*e+c5*T
_[12]=c3*e-4*c4^2*c5*e+12*c4^2*c6*T+4*c4*c5^2*T
-8*c4*c5*c6*e+12*c5^2*c6*T+8*c6^3*T-4*c6*T
_[13]=c2*T-c3*e+c4*T
_[14]=c2*e-c3*T+c5*T-c6*e
_[15]=c1*T+c5*T-c6*e
_[16]=c1*e-c2*T-c6*T
_[17]=c1^2+c2^2+c3^2+c4^2+c5^2+c6^2-1
Table 3: The Gröbner basis of the ideal I + ( f ) . _[1]=4*T^4-5*T^2*U^2+U^4 _[2]=e-U _[3]=12*c6^2*T^2-12*c6^2*U^2-e^2+3*e*U-2*T^2 _[4]=c5*T^2*U-c5*U^3+c6*e^2*T-2*c6*T^3+c6*T*U^2 _[5]=2*c5*T^3-2*c5*T*U^2+c6*e^3-2*c6*e*T^2+c6*T^2*U _[6]=4*c5^2*U-4*c5*c6*T+4*c6^2*e-e _[7]=4*c5^2*T^2-4*c5*c6*e*T-4*c6^2*e*U+8*c6^2*T^2+e*U-2*T^2 _[8]=24*c5^2*c6^2*T-4*c5^2*T-24*c5*c6^3*e+4*c5*c6*e +24*c6^4*T-10*c6^2*T+T _ [ 9 ] = 2 4 * c 5 ^ 4 * T - 1 6 * c 5 ^ 3 * c 6 * e + 1 6 * c 5 ^ 2 * c 6 ^ 2 * T - 10*c5^2*T+8*c5*c6^3*e +2*c5*c6*e-4*c6^2*T+T _[10]=c4*U+12*c5^ 3*T-8*c5^ 2*c6 *e+8*c5*c6^ 2*T- 4*c5*T+4*c6^3*e _[11]=c4*T-c5*e+c6*T _[12]=c3*U-4*c4^2*c5*e+12*c4^2*c6*T+4*c4*c5^2*T-8*c4*c5*c6*e +12*c5^2*c6*T+8*c6^3*T-4*c6*T _[13]=c3*T-c4*e+c5*T _[14]=c2*U-c3*T+c5*T-c6*e _[15]=c2*T-c3*e+c4*T _[16]=c1*U-c2*T-c6*T _[17]=c1*T+c5*T-c6*e _[18]=c1^2+c2^2+c3^2+c4^2+c5^2+c6^2-1 Table 4: Primary ideal decomposition of ideal I + ( f ) . The ideal decomposes into ve primary ideals, each of which is represented by the generators. [1]:(p1)
_[1]=T
_[2]=e
_[3]=c1^2+c2^2+c3^2+c4^2+c5^2+c6^2-1
[2]:(p2)
_[1]=e-T
_[2]=4*c5^2-4*c5*c6+4*c6^2-1
_[3]=c4-c5+c6
_[4]=c3+c6
_[5]=c2+c5
_[6]=c1+c5-c6
[3]:(p3)
_[1]=e+T
_[2]=4*c5^2+4*c5*c6+4*c6^2-1
_[3]=c4+c5+c6
_[4]=c3-c6
_[5]=c2-c5
_[6]=c1+c5+c6
[4]:(p4)
_[1]=e+2*T
_[2]=6*c6^2-1
_[3]=c5+c6
_[4]=c4-c6
_[5]=c3+c6
_[6]=c2-c6
_[7]=c1+c6
[5]:(p5)
_[1]=e-2*T
_[2]=6*c6^2-1
_[3]=c5-c6
_[4]=c4-c6
_[5]=c3-c6
_[6]=c2-c6
_[7]=c1-c6
observable quantities: if we give $T$ , we determine the total energy $U$ and we have the relations for the variables of the wave-function and the eigenvalue $e$ . As for the wave-function, there is a particular feature in the symbolic computation, which will be discussed later.

Now let us see how the primary ideal decomposition works. The decomposition for ideal $I + (f)$ is given in Table 4. Each entry in the list is the primary ideal ${p_{i} | i = 1, ..., 5}$ , the intersection of which shall build the polynomial ideal of secular equation $I = \cap_{(i = 1)}^{5} p_{i})$ .

Table 5 gives the Gröbner basis for the ideal $(p_{i} + (f))$ . Table 5: Gröbner basis for the ideals p_i + (f ) . [1](p1+(f)) _[1]=U _[2]=T _[3]=e _[4]=c1^2+c2^2+c3^2+c4^2+c5^2+c6^2-1 [2](p2+(f)) _[1]=T-U _[2]=e-T _[3]=4*c5^2-4*c5*c6+4*c6^2-1 _[4]=c4-c5+c6 _[5]=c3+c6 _[6]=c2+c5 _[7]=c1+c5-c6 [3](p3+(f)) _[1]=T+U _[2]=e+T _[3]=4*c5^2+4*c5*c6+4*c6^2-1 _[4]=c4+c5+c6 _[5]=c3-c6 _[6]=c2-c5 _[7]=c1+c5+c6 [4](p4+(f)) _[1]=2*T+U _[2]=e+2*T _[3]=6*c6^2-1 _[4]=c5+c6 _[5]=c4-c6 _[6]=c3+c6 _[7]=c2-c6 _[8]=c1+c6 [5](p5+(f)) _[1]=2*T-U _[2]=e-2*T _[3]=6*c6^2-1 _[4]=c5-c6 _[5]=c4-c6 _[6]=c3-c6 _[7]=c2-c6 _[8]=c1-c6 .The first entry gives the linear relation between the total energy $U$ and the hopping parameter $T$ . This is the improvement in the result by the use of primary ideal decomposition; in Table 3 of the Gröbner basis, we have obtained the relation between $U$ and $T$ , but the polynomial is not decomposed yet.

The dimension of the ideals is given in Table 6. (We refer to the Krull dimension of the quotient ring by an ideal by the phrase “dimension of the ideal” according to the custom of computational algebraic geometry.)

As for $p_{1} + (f)$ , the affine algebraic set is determined by $U = T = e = 0$ and $c_{1}^{2} + \dots + c_{6}^{2} = 1$ ; thus there are five degrees of freedom for $(c_{1}, .., c_{6})$ . As for $p_{4} + (f)$ and $p_{5} + (f)$ , the only one indeterminate is the hopping integral $T$ , which contribute one to the dimension of the ideal; $(c_{1}, ..., c_{6})$ is determined up to sign. As for $p_{2} + (f)$ and $p_{3} + (f)$ , the hopping integral $T$ is still an indeterminate and contributes one to the dimension; $(c_{1}, ..., c_{6})$ is not determined explicitly, unless $c_{5}$ or $c_{6}$ would be explicitly given in the quadratic equation in the list (which is one-dimensional geometrical object). In this circumstance, the dimension of the ideal rises by one. The increase of the dimension in the cases of $p_{2} + (f)$ and $p_{3} + (f)$ is, by the familiar phrase of physics, due to the degeneracy in the eigenvalue. For such cases in the numerical computation, the solvers automatically return the ortho-normalized basis vectors. The numerical library determines them by an arbitrary way. However, by summing up the degenerated eigenstates with the equal weights, one can compute the observable quantum mechanical quantity which is free from this sort of ambiguity. In contrast, the symbolic computation processes the equation up to the “minimal” polynomials of the variables of the wave-functions and it does not anymore. The wave-functions are, however, non-observable quantities; one can eliminate them from the polynomial equations by symbolic computation so that one could obtain only observable quantities, such as energy. In fact, it is not always true that the degeneracy of eigenvalues should lead to non-zero-dimensional character of eigenspace: for example, consider the following polynomial as the energy functional:

$f = - c_{1} (c_{2} + c_{3}) - c_{2} (c_{1} + c_{3}) - c_{3} (c_{1} + c 2) + (c_{1}^{4} c_{2}^{4} + c_{2}^{4} c_{3}^{4} + c_{3}^{4} c_{1}^{4}) - e (c_{1}^{2} + c_{2}^{2} + c_{3}^{2} - 1)$

The local energy minima are represented by discrete points (not continuous) both in real and in complex number. For example, $e = - 3 / 2$ is the eigenvalue with six fold degeneracy and the corresponding eigenvectors are discrete (as zero-dimensional ideal) as follows:

$(c_{1}, c_{2}, c_{3}) = \pm (1 / \sqrt{2}, - 1 / \sqrt{2}, 0), \pm (1 / \sqrt{2}, 0, - \sqrt{2}), \pm (0, 1 / \sqrt{2}, - \sqrt{2})$

We have seen how the computational algebraic geometry could be applied to the molecular orbital theory, in so far as the equations could be represented by polynomials. In this section, we will see the related topics on the symbolic computation by means of polynomials.

Polynomial optimization is a numerical method which solves the optimization problem given by polynomial equations and inequities [47,48-51].

Example 8.1 Consider the cost function $g (x_{1}, x_{2}) = x_{2}$ and the constraints $f_{1} = 5 - x_{1}^{2} - x_{2}^{2} \geq 0$ , $f_{2} = 1 - x_{1} x_{2} \geq 0$ , $f_{3} = x_{1} - x_{2} \geq 0$ .

The problem is given by:

Maximize the cost multivariate polynomial function $g (x)$

with the constraint of multivariate polynomial function $f_{i} (x) \geq$ 0.

In other words, the cost function g is to be maximized in the semi-algebraic set defined by $f_{1}$ , $f_{2}$ and $f_{3}$ , as in Figure 5.

The key idea is to replace the monomials $x_{1}^{i} x_{2}^{j}$ with variables $y_{i j}$ . The variables should satisfy relations such as $y_{p, q} y_{r, s} = y_{p + q, r + s}$ and $y_{00} = 1$ . Let us define the first-order moment matrix in the following style:

$M_{1} (y) = (\begin{matrix} 1 & y {}_{10} & y_{01} \\ y_{10} & y_{20} & y_{11} \\ y_{01} & y_{11} & y_{02} \end{matrix})$

By means of the formalism of the polynomial optimization, the problem is restated as follows.

Maximize the linear cost function $y_{01}$ ,
With the constraint that the moment matrix $M_{1} (y)$ is semi-positive definite,
With the constraint of multivariate polynomial functions: ${\hat{f}}_{1} = 5 - y_{20} - y_{02} \geq 0$ , ${\hat{f}}_{2} = 1 - y_{11} \geq 0$ , ${\hat{f}}_{3} = y_{10} - y_{01} \geq 0$

In the above, the constraint of the moment matrix comes from the semi-positive-definiteness of the quadratic form:

$0 \leq (\sum_{i = 1}^{2} c_{i} x_{i}) (\sum_{i = 1}^{2} c_{i} x_{i}) ≃ \sum_{i, j} c_{i} c_{j} y_{i j}$

Hereafter we denote the semi-positive definiteness of a matrix $M$ as $M ≽ 0$ .

The optimization problem is solved by the standard way of semi-positive-definite programming. We can formulate the dual problem also. In general, it is not guaranteed that the use of the first-moment matrix would suffice to give the correct answer; indeed the formulation should be given in the matrices of infinite dimension, which include the moments of higher orders up to the infinity. In addition, in the above formulation, there is no constraint for the condition $y_{p, q} y_{r, s} = y_{p + q, r + s}$ . We only expect that the moment matrix would be reduced into the one with lower and suitable rank at the optimum. Actually, the above procedure is an approximation and the accuracy is improved by the use of larger matrices.

Let $y = {(y_{α})}_{α \in ℕ^{n}}$ , where $y_{α}$ represents $x^{α} = x_{1}^{α_{1}} ... x_{n}^{α_{n}}$ . Let denote the degree of $(y_{α})$ as $| α | = \sum_{i = 1}^{n} α_{i}$ . We try to optimize the problem in the limited range of ${(y_{α})}_{α \in ℕ^{n}}$ , such that $| α | \leq 2 r$ .

For $y = (y_{α_{1}}, y_{α_{1}}, ..., y_{α_{N}})$ (such that $| α_{N} | \leq 2 r$ ), the r-th order moment matrix $M_{r} (y)$ is constructed as follows:

$M_{r} (y) [1, 1] = 1$ ,
$M_{r} (y) [i, 1] = y_{α_{i}}$ ,
$M_{r} (y) [1, i] = y_{α_{i}}$ ,
$M_{r} (y) [i, j] = y_{α_{i} + α_{j}}$

where the index i,j are taken in the range such that $| α_{i} | \leq r$ .

Let $p (x)$ be the polynomial constraint :

$p (x) = \sum_{b e t a} c_{β} x^{β}$

For $p (x)$ , the localizing matrix is defined by:

$M_{s} (p y) [i, j] = \sum_{β} c_{β} y_{α_{i} + α_{j} + β}$

where the index $i, j$ are taken in the range such that $| α_{i} | \leq s$ . This matrix should be semi-positive definite, too. In general, a global polynomial optimization problem is given by

$p * = \min_{y} F (x) = \sum_{α} f_{α} x^{α}$

such that $G_{i} (x) \geq 0$ , $i = 1, 2, ...$ .

Assume that the degree of $g_{i} (x)$ to be $2 d_{i} - 1$ or $2 d_{i}$ . In correspondence to the above global polynomial problem, The relaxation of order k is stated in this way:

$p_{k} * = \min_{y} \sum_{α} f_{α} y^{α}$

such that $M_{k} (y) ≿ 0$

and $M_{k - d_{i}} (G_{i} y) ≿ 0$ , $i = 1, 2, ...$

It is guaranteed that, as the degree $k$ increases, the optima $p_{k}^{*}$ converges to the global optimum p.

Example 8.2 Let us compute these matrices.

The second-order moment matrix is given by

$M_{2} (y) = (\begin{matrix} 1 & y_{10} & y_{01} & y_{20} & y_{11} & y_{02} \\ y_{10} & y_{20} & y_{11} & y_{30} & y_{21} & y_{12} \\ y_{01} & y_{11} & y_{02} & y_{21} & y_{12} & y_{03} \\ y_{20} & y_{30} & y_{21} & y_{40} & y_{31} & y_{22} \\ y_{11} & y_{21} & y_{12} & y_{31} & y_{22} & y_{13} \\ y_{02} & y_{12} & y_{03} & y_{22} & y_{13} & y_{04} \end{matrix})$

The higher-order moment matrices are computed likewise.

The localizing matrices are computed for the polynomials $f_{1}$ , $f_{2}$ and $f_{3}$ in the example problem. For $f_{1} = 5 - x_{1}^{2} - x_{2}^{2}$ ,

$M_{1} (f_{1} y) = (\begin{matrix} 5 - y_{20} - y_{02} & 5 y_{10} - y_{30} - y_{12} & 5 y_{01} - y_{21} - y_{03} \\ 5 y_{10} - y_{30} - y_{12} & 5 y_{20} - y_{40} - y_{22} & 5 y_{11} - y_{31} - y_{13} \\ 5 y_{10} - y_{21} - y_{02} & 5 y_{11} - y_{31} - y_{13} & 5 y_{02} - y_{22} - y_{04} \end{matrix})$

For $f_{2} = 1 - x_{1} x_{2}$ ,

$M_{1} (f_{2} y) = (\begin{matrix} 1 - y_{11} & y_{10} - y_{21} & y_{01} - y_{12} \\ y_{10} - y_{21} - y_{20} & y_{20} - y_{31} & y_{11} - y_{22} \\ y_{01} - y_{12} & y_{11} - y_{22} & y_{02} - y_{13} \end{matrix})$

For $f_{3} = x_{1} - x_{2}$ ,

$M_{1} (f_{2} y) = (\begin{matrix} y_{10} - y_{01} & y_{20} - y_{11} & y_{11} - y_{02} \\ y_{20} - y_{11} & y_{30} - y_{21} & y_{21} - y_{12} \\ y_{11} - y_{02} & y_{21} - y_{12} & y_{12} - y_{03} \end{matrix})$

Observe that these localizing matrices include the entries of the second order moment matrix and do not contain superfluous ones. We can optimize the given problem concisely with the use of $M_{2} (y)$ , $M_{1} (f_{1} y)$ , $M_{1} (f_{2} y)$ , $M_{1} (f_{3} y)$ .

As is demonstrated in [2], once the molecular orbital theory has been built over the polynomial system on the ground of algebraic geometry and commutative algebra, it enables us to joint the equation of conventional quantum mechanics and the extra constraints into a set of polynomial equations. We solve the problem through the collaboration of numerical and symbolical methods. The computational scheme is basically to determine the affine algebraic set described by the set of equations. However, it is somewhat inconvenient that we should use only equations for the general optimization problem. It seems that polynomial optimization could get over such limitations because it could deal with the constraints by inequities in the semi-algebraic set. The mathematical ground is “real algebraic geometry” which contains a various range of interests.

When we deal with equations and inequities of polynomials, we often ask ourselves about the existence of the solutions. For example, under what condition would a quadratic equation have roots? The “quantifier elimination” (QE) is the computational process to answer this sort of questions: when the question is given by $\exists x \in ℝ . (x^{2} + b x + c = 0)$ , the computer eliminates the quantifier ( $\exists$ ) and returns the simplified form $b^{2} - 4 a c \geq 0$ as the answer. In fact, there are general theories for executing such sort of simplifications, proposed by several mathematicians, such as by Fourier, by Motzkin, and by Tarski [52,53], or Presburger arithmetic. But those algorithms are not practical. Afterward, more practical algorithms by Collins and by others have come into use, called “Cylindrical Algebraic Decomposition” (CAD). The theoretical ground of the standard algorithm in Algebraic Cylindrical Decomposition are given in [46,54-58]. There are several computer packages in which this algorithm is implemented, such as QEPCAD [59], Mathematica [60], Maple [61], and Reduce [62]. Since CAD algorithm is apparently related to the theme of this article, let us review the computational procedure in this section. Let us consider the problem through a simpler example of quantifier elimination: $\exists a . (x^{2} + a x + 1 = 0)$ .

We can simplify the above prenex form into the one without quantifier, such as $a^{2} - 4 \geq 0$ .

The cylindrical algebraic decomposition analyses the critical point of $f (a, x) = x^{2} + a x + 1 = 0$ in two-dimensional real $a - x$ plane. The critical points are the solutions of $f (a, x) = x^{2} + a x + 1 = 0$ and $\frac{\partial f (a, x)}{\partial x} = 2 x + a$ . They are also the solution of $x^{2} + a x + 1 = 0$ , $2 x + a = 0$ and $x (2 x + a) = 0$ . Thus we obtain the matrix equation:

$(\begin{matrix} 1 & a & 1 \\ 2 & a & 0 \\ 0 & 2 & a \end{matrix}) (\begin{matrix} x^{2} \\ x \\ 1 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix})$

The determinant of the matrix in the left-hand side is the discriminant of $f (a, x)$ . If it is zero, the matrix equation would permit non-zero vector solution. Hence we project the polynomial in one ring into a polynomial in another ring of lower dimension (Projection step). We now analyse the projected polynomial (the discriminant) in order to inquire after the existence of the root. As the discriminant is $4 - a^{2}$ , we can divide the $a -$ axis into five cells: $(- \infty, - 2), {- 2}, (- 2, 2), {2}, (2, \infty)$ so that each of them gives the distinct sign of the discriminant.

Let us build the set of cylinders in a-x plane which pass through each cells in a-axis. They are given by

$(a, x) \in (- \infty, - 2) \times (- \infty, \infty)$ ,

$(a, x) \in {- 2} \times (- \infty, \infty)$ ,

$(a, x) \in (- 2, 2) \times (- \infty, \infty)$ ,

$(a, x) \in {2} \times (- \infty, \infty)$ ,

$(a, x) \in (2, \infty) \times (- \infty, \infty)$ .

In each cylinder, we should check the zeros and the sign condition of $f (a, x) = x^{2} + a x + 1$ in $a - x$ plane. The solutions of $f (a, x)$ are listed as follows.

$a \in (- \infty, - 2)$ : the solutions are $x_{1} = (- a - \sqrt{a^{2} - 4}) / 2$ and $x_{1 x_{2} = (- a + \sqrt{a^{2} - 4}) / 2} = (- a - \sqrt{a^{2} - 4}) / 2$ .
$a = - 2$ : the solution is $x_{1} = 1$ .
$a \in (- 2, 2)$ : no solution.
$a = 2$ : the solution is $x_{1} = - 1$
$a \in (- 2, \infty)$ : the solutions are $x_{1} = (- a - \sqrt{a^{2} - 4}) / 2$ and $x_{2} = (- a + \sqrt{a^{2} - 4}) / 2$ .

(In the actual computation, we do not try to obtain such analytic solutions in uplifting step. Instead, we place one sampling point, say , in each subdivision, and we inspect the sign condition and the solution of univariate polynomial $f (a_{s}, x)$ . )

The cylinders are again divided into cells according to the sign condition of $f (a, x)$ . For example, the cylinder $(- \infty, - 2) \times (- \infty, \infty)$ is divided by five cells:
$(- \infty, - 2) \times (- \infty, x_{1})$ ;
$(- \infty, - 2) \times {x_{1}}$ ;
$(- \infty, - 2) \times (x_{1}, x_{2})$ ;
$(- \infty, - 2) \times {x_{2}}$ ;
$(- \infty, - 2) \times (x_{2}, \infty)$ .

For other cylinders, we construct the cells likewise, as is illustrated in Figure 6. These cells in a-x plane are distinguished by the sign conditions of $f (a, x) = x^{2} + a x + 1$ and $dis (f) = 4 - a^{2}$ . Then we seek the cells which would satisfy the condition of the first question about the existence of the roots of $x^{2} + a x + 1 = 0$ , and by joining the cells which satisfy the requirement, we find the answer: $a \leq - 2$ or $a \geq 2$ .

In general multivariate case of CAD, the algorithm executes the multi-step projection (from n-variables to one-variable ) and uplifting (from an axis to the whole space).

There are examples of QE with the taste of molecular orbital theory. Let $e, (x, y)$ be the energy and the wavefunction of the simple diatomic system, such that

$\begin{array}{r} (\begin{matrix} 0 & - 1 \\ - 1 & 0 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = e (\begin{matrix} x \\ y \end{matrix}) \end{array}$

Example 8.3 $\exists e : e < 0 \land x + e y = 0 \land y + e x = 0 \land x^{2} + y^{2} - 1 = 0 \land x + y = 0..$

The prenex form inquires if the negative e (the energy) would exists in the diatomic molecule of asymmetric configuration $x + y = 0$ . The quantifier elimination concludes that the formula is
$F a l s e .$

Example 8.4 $\exists e : e < 0 \land x + e y = 0 \land y + e x = 0 \land x^{2} + y^{2} - 1 = 0 \land x - y = 0$

The prenex form inquires if the negative e (the energy) would exists in the diatomic molecule of symmetric configuration $x - y = 0$ . The quantifier elimination concludes that the formula is simplified as
$x^{2} + y^{2} - 1 = 0 \land x - y = 0$

This is the process of quantifier elimination. If the prenex form contains several polynomials ${f_{j} (x_{1}, x_{2}, ..., x_{n}) | j = 1, ..., m}$ , we have to compute the intersection of $f_{i}$ and $f_{j}$ for $i \neq j$ as well as the critical point of each $f_{i}$ . The intersection is computed by projection by means of variable elimination, the tool of which is “resultant”. Assume that ${f_{j}}$ are the uni-variate polynomials of $x_{n}$ , in which the coefficients are the polynomials of ${x_{1}, .., x_{n - 1}}$ . In this assumption, the resultant for two polynomials
$A = a_{0} x^{d} + a_{1} x^{d - 1} + \dots + a_{d}$
and
$B = b_{0} x^{e} + b_{1} x^{e - 1} + \dots + b_{e}$
is the determinant of a square matrix of dimension d+e, defined as
$(\begin{matrix} a_{0} & a_{1} & \dots & a_{d} & 0 & \dots & 0 \\ 0 & a_{0} & \dots & a_{d - 1} & a_{d} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & a_{0} & a_{1} & \dots & \dots & a_{d} \\ b_{0} & b_{1} & \dots & b_{e} & \dots & \dots & 0 \\ 0 & b_{0} & \dots & b_{e - 1} & \dots & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ & \dots & ⋱ & ⋮ \\ 0 & 0 & b_{0} & b_{1} & \dots & \dots & b_{e} \end{matrix})$
in which the rows are made from the array of coefficients of ${x^{i} A | i = e - 1, .,,, 0}$ and ${x^{j} B | j = d - 1, ..., 0}$ so that the product of the matrix and the vector $(x^{d + e}, x^{d + e - 1}, ..., x, 1)$ should give those set of polynomials. The discriminant of $f (x)$ is a special case as the resultant of $f (x)$ and $\frac{d f (x)}{d x}$ .

We expect that quantifier elimination would be applicable to the molecular orbital theory when we give the polynomial representation to the problem. If the quantifier elimination goes well, we would obtain the polynomial representation of the solution of the optimization problem; we could render the zone and the boundary in the parameter space which shall satisfy our requirement; we might “reason” for the question of quantum mechanics by means of the rigorous foundation of logic. However, at present, the computer and the algorithm are still powerless; indeed the complexity of the algorithm, in the worst case, is double exponential in the number of variables . (This is because of the enormous number of combinations of polynomials in the process of variable-elimination.) Therefore we must expect some breakthrough both in algorithm and in computer architecture in order that we could apply quantifier elimination for the practical purpose.

In the above examples, we implicitly assume that all of the required ingredients are polynomials. They are generated by the method of quantum chemistry: by the use of localized atomic basis, the integrodifferential equation is converted into the secular equation of analytic functions, and the latter is furthermore approximated by polynomials. On the other hand, the fundamental equations of quantum mechanics always involve differential operators. Indeed the symbolic computation would be applicable to the algebra generated by variables and differentials (G-algebra); the Gröbner basis could be computed by extending the Buchberger’s algorithm (Mora’s algorithm [77])). However, G-algebra is rather a purely mathematical topic and it seems to be powerless in solving numerical problems.

For this issue, the aforementioned polynomial optimizations would give us some hint. The key idea is to replace the monomials in the equation with the variables of one-degree, and the latter variables are determined by the framework of semi-positive definite programming [78].

The algorithm of polynomial optimization is based on the measure theory. The variables of degree one, corresponding to the monomials $X^{α} = x_{1}^{α_{1}} \cdot x_{2}^{α_{1}}$ , represent the integrals in the moment problem, $y_{α} = \int^{} X^{α} d μ$

by means of some probability measure $μ$ , which satisfies $\int^{} d μ = 1$ . We construct the entry of the moment matrix in the following form
$y_{α, β} = \int^{} X^{α} X^{β} d μ$

Instead of directly determining the measure, however, the algorithm computes the moments $y_{α, β}$ by utilizing the constraints among them so that the objective function would be maximized.

This foundation of the algorithm has a great significance: it is plausible that, if we inspect the problem from the analogy of quantum mechanics, the measure $d μ$ might be replaced by $| ϕ (x) |^{2} d x$ by a certain “wavefunction” $ϕ$ , and the moments will be given by the expectation value in the sense of quantum mechanics. As the expectation values of the products of coordinate operators and the differential operators can be computed, we can extend the idea of the moment matrix. For the univarite case, the typical integrals are given by
$y_{i j} = (ϕ | x^{i} x^{j} | ϕ)$
or
$y_{i : j} = (ϕ | x^{i} {(\frac{\partial}{\partial x})}^{j} | ϕ)$ .

Let us consider the simplest problem: the harmonic oscillator.

The total energy of the harmonic oscillator is given by the sum of squares of the kinetic-momentum operator p and the coordinate operator $x : H = p^{2} + x^{2}$ , with the relation:

$[p, x] = - \sqrt{- 1} h$

In order to avoid the argument in the complex number, we make use of $u = h d / d x$ , instead of $p$ .

We define the extended moment matrix as
$M [x^{i} u^{j}] [x^{k} u^{l}] = \int^{} (x^{i} u^{j} ϕ) (x^{k} u^{l} ϕ) d x$

This sort of integral is rearranged by the linear combination of those terms
$M [x^{m} u^{n}] = \int^{} ϕ (x^{m} u^{n} ϕ) d x$

The the moment matrix (indexed by $1, x, u$ ) is given as:
$(\begin{array}{l} 1 & M [x] & 0 \\ M [x] & M [x x] & - h / 2 \\ 0 & - h / 2 & M [- u u] \end{array})$

(In the above, $M [- u u] = - M [u u]$ due to the linearity of the constant.) In order to compute that matrix, we have used use the relations:

$M [u] [1] = \int^{} (h \frac{d}{d x} ϕ) ϕ d x = 0$
$M [u] [u] = \int^{} (h \frac{d}{d x} ϕ) (h \frac{d}{d x} ϕ) d x = \int^{} ϕ (- h^{2} \frac{d^{2}}{d x^{2}} ϕ) d x = M [- u u]$
$\begin{array}{r} M [u] [x] & = & \int^{} (h \frac{d}{d x} ϕ) (x ϕ) d x = \int^{} ϕ (- h \frac{d}{d x} \cdot x) ϕ d x = - M [u x] \\ = & \int^{} ϕ (- h - x \frac{d}{d x}) ϕ d x = - M [x u] - h . \end{array}$

In order to see the necessity of $h / 2$ , let us consider the quadratic form:
$\int^{} [(a u + b x) ϕ] [(a u + b x) ϕ] d x (\geq 0)$

This quadratic form is represented by

$\begin{array}{r} - a^{2} M [u u] + b^{2} M [x x] + a b (- M [u x] + M [x u]]) \\ = & - a^{2} M [u u] + b^{2} M [x x] - a b h \\ = & (a, b) (\begin{array}{l} M [- u u] & - h / 2 \\ - h / 2 & M [z z] \end{array}) (\begin{array}{l} a \\ b \end{array}) (\geq 0) \end{array}$

The semi-positive definiteness of the quadratic form is replaced by that of the matrix.

Semi-positive definiteness of the moment matrix demands these relations:

$M [x x] \geq 0$
$M [- u u] \geq 0$
$M [x x] M [- u u] - \frac{h^{2}}{4} \geq 0$
$\det (M) \geq 0$
$M [x x] - M [x] M [x] \geq 0$

(The diagonal entries of the matrix are positive; the values of determinant of 2 by 2 minors, taken along the diagonal, are positive; and the determinant of the matrix is positive.)

With this condition, the optimum of $E = M [- u u] + M [x x]$ is obtained at $M [x x] = M [- u u] = \frac{1}{2} h$ and $M [x] = 0$ . The solution might be obtained by several methods. The authors of this article (Kikuchi and Kikuchi) had tried several algorithms to solve them in the sequence of works: the solution by means of QE in [63]; by means of particle swarm optimization in [64]; by means of directly determining the measure μ itself in [65].

Maybe the significance of this algorithm is that one can “quantize” the polynomial equations by providing the variables ${x_{i}}$ with the differential operators ${h \frac{d}{d x}}$ ; the search of the roots of the polynomial $W (x)$ is replaced by the ground-state computation of the quantum Hamiltonian $H = - h^{2} \frac{d^{2}}{d x^{2}} + W (x)$ ; in the limit $h \to 0$ , the “probability distribution” of the quantum system shall coincide with the affine algebraic set $V (W)$ . It is not so audacious to say that we discover the seminal idea of “wave geometry”, which is the counterpart in mathematics to the “wave mechanics” in physics. In the middle of twentieth century, in fact, Mimura et al. proposed the idea of “wave geometry” [66]: their fundamental idea is to assume the line elements $d s^{2}$ in differential geometry as the operator in quantum mechanics, to which, therefore, the differential operator $h \frac{d}{d s}$ is coupled. In contrast to that theory, our idea of “wave geometry” is based upon algebraic geometry, and we expect that our idea would be applicable to quantitative – numeric or symbolic – computation by means of powerful techniques developed for quantitative simulation of quantum dynamics and also by means of the modern theory of algebra.

There are several packages of symbolic computation by which we can compute Gröbner bases or primary ideal decomposition.

CoCoA : Computer algebra system [67].
GAP: Software for computational discrete algebra. The chief aim of the package is to execute the computation in the group theory, but it could process polynomials [68]. As for the application of GAP software in material physics, see the work of Kikuchi [77], and the article by Kikuchi and Kikuchi [69].
Macaulay 2: Computer algebra system [70, 71].
Mathematica: Technical computing system for almost all fields of science and industry [60].
Maple: Symbolic computation software for general purpose. The primary ideal decomposition is implemented at the package “Regular Chains Package” [61].
Maxima: Symbolic computation software for general purpose [72].
Reduce: Computer algebra system [62].
SINGULAR: Computer algebra system [73]. It contains various libraries to solve the problems in algebraic geometry. It also contains the extension package “Plural” for non-commutative algebra. One can learn how to compute by Singular from introductory textbooks [40,74].
As for quantifier elimination, also there are available packages.
QEPCAD: A free software, which does quantifier elimination by means of Partial Cylindrical Algebraic Decomposition [59].
Reduce
Mathematica
Maple

There is a platform system which bundles several free software packages in mathematical science.

SageMath: Open-Source Mathematical Software System. From this platform, one can utilize a lot of software packages both of numerical and symbolic computations (in which Gap, Maxima, and Singular are included) [75].

There are a lot of research centers of symbolic computations. A great deal of computer algebra systems are the products of the studies over long years in several universities. One can find software implementations of the latest researches of INRIA in France:

INRIA: l’institut national de recherche dédié aux sciences du numérique. The research programs, at the interplay of algebra, geometry and computer science, are ongoing now [76].

Dear readers, our voyage has now ended up the planned course. How do you think about the connection between quantum mechanics and algebraic geometry? We have found it even in the familiar region of quantum chemistry. Algebraic geometry is not a language of another sphere; it is a tool to solve actual problems with quantitative precision. Is it interesting for you? Or have you judged coldly that it is a plaything?

In this article, at first, we have demonstrated a model case of symbolic-numeric computation of molecular orbital theory with the taste of algebraic geometry. Then we have expounded the related mathematical concepts in commutative algebra and algebraic geometry with simple examples. In addition, we have introduced several mathematical and computational methods, which would be connected to this post-contemporary theory of quantum chemistry. The two main principles of the theory are to represent the involved equations by polynomials and to process the polynomials by computer algebra. Then one can analyze the polynomial equations and unravel the dependence between the variables. In the traditional molecular orbital theory, the principal mathematical tool is the linear algebra. Indeed, it is a subset of the commutative algebra. For instance, the diagonalization of the matrix and the orthonormality of eigenstates would be comprehensible in a wider context: the primary ideal decomposition. And the latter has a close relation to the other fundamental ideas in algebraic geometry: the resolution of singularity and the normalization of the variety. Besides, the polynomial approximation (inevitable in our theory) should ideally be embedded into the “completion” of commutative rings; we do this approximation with the finite number of symbols for the sake of facile computations in the limited resources. Without doubt, there are a lot of other concepts in commutative algebra and algebraic geometry which would be embodied in the application of computational quantum mechanics. You should Ask, and it will be given to you...

Or,

petite, et dabitur vobis; quaerite, et invenietis; pulsate, et aperietur vobis. It will be a felicity for us, for the authors of this article, if you enjoy every bite of the “quantum chemistry with the view toward algebraic geometry” and if this article stirs your curiosity; we heartily greet your participation in the research of this new theme.

The authors are grateful to all readers who have spent the precious time to accompany with the authors through the seemingly “arid” topics toward the end of the article.

Supplementary File

	Solution 1	Solution 2	Solution 3	Solution 4
t	-0.53391	0.00000	-0.53391	0.00000
s	0.00000	-1.42566	0.00000	-1.42566
u	-0.53391	-0.53391	0.00000	0.00000
v	0.00000	0.00000	-1.42566	-1.42566
ev	-0.62075	-0.01567	-0.62734	0.01884
ew	-0.62075	-0.62734	-0.01567	0.01884
r	1.40000	1.40000	1.40000	1.40000
The total energy	-1.09624	-0.49115	-0.49115	0.15503
electron 1	symmetric	asymmetric	symmetric	asymmetric
electron 2	symmetric	symmetric	asymmetric	asymmetric

Ideal	${dim}_{k} (R/I)$
$p_{1} + (f)$	5
$p_{2} + (f)$	2
$p_{3} + (f)$	2
$p_{4} + (f)$	1
$p_{5} + (f)$	1

Computational Algebraic Geometry and Quantum Mechanics: An Initiative toward Post Contemporary Quantum Chemistry

Abstract

Keywords

Abstract

Keywords

Introduction

Basics of Commutative Algebra and Algebraic Geometry

Polynomial and ring

Example 4.1

Example 4.2

Ideal

Affine algebraic set (Affine algebraic variety)

Residue class ring or quotient ring

Prime and primary ideal

The correspondence between variety and ideal

Noetherian ring

Dimension and Krull dimension

Zero-dimensional ideal

Nullstellensatz

Spectrum of ring and Zariski topology

Unique factorization domain

Completion: formal description of Taylor expansion

Localization

Integrality

Normalization

Hensel’s lemma

Real algebraic geometry

Definition 4.16

Example 4.46

Noether normalization

Differential Galois theory

Other important concepts of commutative algebra

Gröbner Basis Theory

The monomial orders

Initial ideal

Definition of Gröbner basis

Buchberger’s algorithm

Gröbner basis of zero-dimensional ideal

Syzygy

Church-Rosser property

Complexity of the Gröbner basis algorithm

Gröbner basis for modules

Application of Gröbner basis

Gröbner basis algorithm in a different light

Stickelberger’s theorem

Algorithm of computing Krull dimension

Algorithm for the decomposition of the ideal as eigenvalue solver

Primary ideal decomposition

Algorithm of Gianni, Trager, and Zacharias

Definition 6.1

Triangulation of polynomial system

Simple Example of The Molecular Orbital Method by Means of Algebraic Geometry

Outlook for Related Topics

Polynomial optimization

Quantifier elimination

Polynomial optimization and wave-geometry

Available Packages of Symbolic Computation

Summary

Acknowledgment

Contact Journal

Guidelines

Quick Links

Subscribe