Journal Name: Journal of Multidisciplinary Research and Reviews
Article Type: Research
Received date: 01 November, 2018
Accepted date: 12 November, 2018
Published date: 19 November, 2018
Citation: Gouda OE, Amer GM, Salim OM, Elsayed EA. (2018) Techniques used for Unequally Spaced Grounding Grid Design. J Multidis Res Rev. Vol: 1, Issu: 1 (01-09).
Copyright: © 2018 Gouda OE. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Grounding system is one of the most important items of the power plants and substation systems design. The main purpose of power system substation grounding grids is to maintain reliable operation and provide protection for personnel and equipment during fault conditions. In any substation planning, economical and effective grounding system plays an essential role since absence of effective grounding grid can result in mal-operation of protective devices and hazardous for operators and substation equipment. Therefore, in this paper, the evolutional technique for unequally spaced grounding grid design is suggested. The design is based on hybridization of optimum compression ratio (OCR) and particle swarm optimization (PSO) techniques. This approach is purposed to control the grounding copper volume of the grounding system with the aid of controlling of unequally spaced grounding conductor lengths with respect to the safety measures. The proposed technique offers almost 20% of copper savings comparing with the optimum compression ratio method.
Keywords
Ground grid, Optimum compression ratio, Particle swarm optimization, Ground potential rise, Step voltage, Touch voltage.
Abstract
Grounding system is one of the most important items of the power plants and substation systems design. The main purpose of power system substation grounding grids is to maintain reliable operation and provide protection for personnel and equipment during fault conditions. In any substation planning, economical and effective grounding system plays an essential role since absence of effective grounding grid can result in mal-operation of protective devices and hazardous for operators and substation equipment. Therefore, in this paper, the evolutional technique for unequally spaced grounding grid design is suggested. The design is based on hybridization of optimum compression ratio (OCR) and particle swarm optimization (PSO) techniques. This approach is purposed to control the grounding copper volume of the grounding system with the aid of controlling of unequally spaced grounding conductor lengths with respect to the safety measures. The proposed technique offers almost 20% of copper savings comparing with the optimum compression ratio method.
Keywords
Ground grid, Optimum compression ratio, Particle swarm optimization, Ground potential rise, Step voltage, Touch voltage.
Introduction
The short-time large ground fault currents will make the power systems unstable and meantime be danger to persons and network equipment. Hence, the grounding grid design should consider the constraints of the step voltage, touch voltage, ground potential rise (GPR), and ground resistance for the sake of safety. In modern substations, the grounding system is an essential part of the overall electrical system; its design has very much importance [1,2].
According to IEEE 80 standard [2], the grounding grid resistance must be low enough to assure that faults currents dissipate through the grounding grid into the earth, while the ground potential rise on the earth’s surface must be kept under certain tolerances. [2].
As it is known the person’s safety which is one of the main goals of the grounding systems is usually affecting by the ground potential rise (GPR) and step and touch voltages of grounding grid structure during grounding faults of electrical networks [3-9]. In order to limit the GPR to safe values, it is necessary to design a right grounding grid that effectively connects with the metallic structure of the substation to ensure the safety criteria [10-12]. Some of the investigators and designers suggested unequally spaced grids as a method to save about 34% of grounding grid material [13-15].
Some parameters of grounding grids such as grounding resistance and step and touch voltages can be calculated using simplified assumptions and some of these parameters are difficult to be calculated by simplified method but they are determined by using experimental techniques [16-17]. Some investigators have proposed formulas to calculate the earth surface potential, touch voltage, step voltage and grounding resistance. Others used the charge simulation method to carry out the same calculations [18- 19]. Experimental models are used to obtain the same parameters by other investigators [20-22].
The optimal design of grounding systems for the substations is to suitably arrange the conductors of grounding systems to equalize the leakage current distribution and the potential gradient of ground surface; while keeping the step and maximum touch voltages within the safe limits; this would ensure making all grounding conductors sufficiently utilized so certified as a safe and economic design method. IEEE 80-2000 standard is used in the design of safe grounding grid. Based on this standard software, programs are designed and used in choosing the economical design and installation of substations grounding system through a lot of alternatives [23-25]. Optimum design of grounding system in uniform and non-uniform soils using ANN is presented by Gouda et al. [26]. Optimized design of substation grounding system using newly developed IEEE compliant software is reported by Vyas et al. [27]. Optimal design of the grounding grid by FEM considering different layered soil models is reported by Anton [28].
Recently, new techniques are used in the design of the most economical grounding system [29-36]. Designing of the grounding grid system having safety and grounding resistance requirements with the lowest cost is a nonlinear problem with relative minimum points. Some techniques have been proposed to achieve this goal. One of these techniques is the optimum compression ratio (OCR). Many studies of grounding grid design have been planned on the trial-and-error approaches. These approaches make the mesh dimension of the grounding grid satisfy with constraints of the touch voltage, step voltage, GPR and grounding resistance from standards. In this paper design of unequally spaced grounding grid by hybridization of Optimum Compression Ratio (OCR) and Particle Swarm Optimization (PSO) Techniques, is suggested. As it is known PSO is a powerful scheme for the solution of similar problems. The proposed technique proved that it is suitable for determining the best design of a substation grounding system. It offers almost 20% of copper savings comparing with the unequally spaced traditional methods.
Methods used in the Design
Optimum Compression Ratio (OCR)
The conductor compression ratio “C” is related to the grid dimensions and the maximum conductor separation dmax which occurs toward the center of the grid and is given by:
Where N is the desired number of conductors perpendicular to a given grid axis of length L. When the grounding conductors are arranged according to an exponent regularity, the conductors span decreases gradually from the center to the side of the grounding grid. The ith conductor span from the center is
For the optimal design of grounding grids, the optimum compression ratio can be used, in which the touch voltage reaches its minimum value if the grounding grid is designed under this compression ratio [37]. Grid conductors of unequally spaced grid having denser conductors at the edges proved the most safe and efficient design [38-40]. However, one merit of the use of unequally spaced grid produces more uniform current density in the grid conductors and therefore remarkable decrease in the voltage gradients of the earth’s surface is reported [41-44]. Then, the touch voltage for such grid reaches its lowest values and thus the conditions of safety for human above the earth surface of the substation will be ensured. It is concluded by [42] that the use of unequally spaced grid using OCR technique saves about 34% of grounding grid material. Sequentially the cost of the installation of the grid will be reduced. An empirical expression is obtained to calculate OCR as follows [23].
Where
Where k is the segments number of the conductor in any direction; h is the laying depth of the grid. The relationship between a0, a1... and L is given in Table 1 [23].
Table 1: Relationships between a0, a1, a2 and L.
| Coefficients | L ≤ 100 m | 100 m ≤ L ≤ 175 m | 175 m ≤ L ≤ 250 m | L>250 m |
|---|---|---|---|---|
| a01 | 0.44 | 0.38 | -0.51 | 0.32 |
| a02 | -77.43 | -50.65 | -33.18 | -15.44 |
| a03 | 15.63 | 13.88 | 18.49 | 13.42 |
| a11 | 0.033 | 0.19 | 1.15 | 0.38 |
| a12 | 76.9 | 50.21 | 32.82 | 15.16 |
| a13 | -15.56 | -13.83 | -18.44 | -13.38 |
| a21 | -0.067 | -0.037 | -0.029 | -0.022 |
| a22 | 0.5 | 0.41 | 0.34 | 0.26 |
Particle Swarm Optimization (PSO) algorithms
The (PSO) Particle Swarm Optimization is defined as a multi-agent search technique that ensures a swarm of particles and each particle performs a prospect solution in the swarm. All the particles fly meanwhile multidimensional the search space. Each particle is regulating its position with respect to its own practice and the experience of neighbors [45]. Therefore, in a PSO technique, all particles are beginning randomly and estimated to compute fitness together with finding the personal best and global best. After that, a loop starts to find an optimum solution. In the loop, first the particles’ velocity is updated by the personal and global bests, and then each particle’s position is updated by the current velocity. The loop is ended with a stopping criterion predetermined in advance. Basically, two PSO algorithms, namely the Global Best (Gbest) and Local Best (Lbest) PSO, have been developed which differ in the size of their neighborhoods [45].
Voltage profile computation by using image method
By using the Infinite Series Potential Method (I.S.M) [8,9], the potential difference in volts can be calculated in three dimensions (x, y, z) using the following equation.
Where
Where I is the short circuit current in ampere, l is grid side length in meter and ρ is the soil resistivity in Ωm [20, 21]. If there is a grid of total conductor length (LC) buried in uniform soil, the total potential differences (VTotal) caused by this grid; means interference between any point and all conductors of the grid and its images, it will be the sum of the potential caused at this point by this grid conductors and all its images [44].
Design of Unequally Spaced Grounding Grid using Optimal Compression Ratio (OCR)
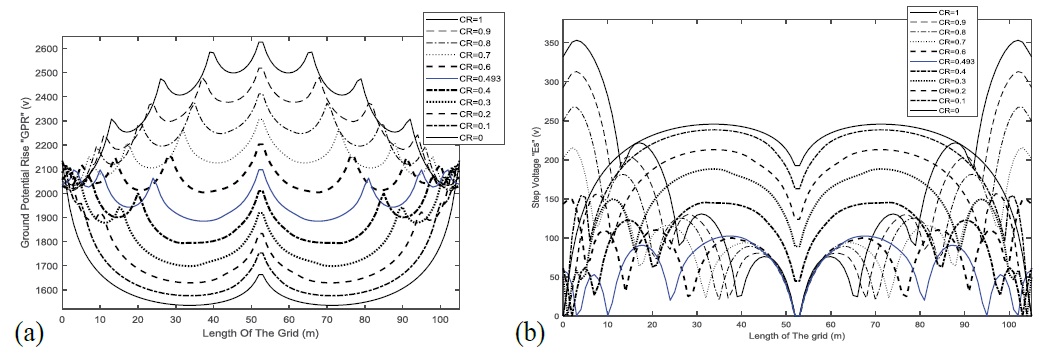
The safe design of the unequally spaced grounding grid system should limit the ground potential rise (GPR), step and touch potentials of grounded structures during electric power faults to safe values, besides reaching to the predetermined value of the grounding resistance. In this paper, the ground potential rise, step voltage and touch voltage are calculated along the center conductor for unequally spaced grid area A=105 × 105 m2 having 64 meshes. Figures 1(a) and (b) give the unequally spaced grid ground potential rise (GPR) and step potential of grounding grid structure along the center conductor in case of unequally spaced grid having denser conductors at the edges under different values of compression ratios (CR) when the short circuit current is 10 kA and the soil resistivity is 100 Ωm.
Figure 1: The ground grid potential rise and step potential versus the compression ratios (a) The ground grid potential rise (GPR) and (b) step potential along the center of the square grounding grids.
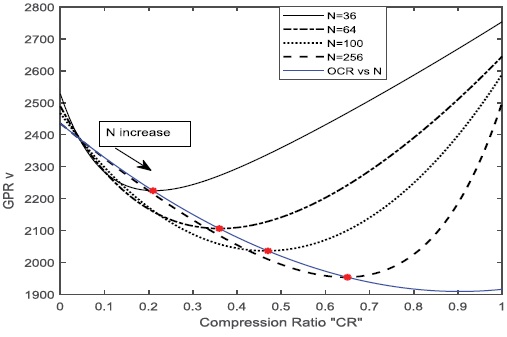
Figure 2: The relation between the meshes number, GPR and the value of OCR.
Summary of the relations between the grid ground potential rise (GPR), step and touch potentials and grid resistance from one side and the compression ratios on the other side is given in Table 2. By the analysis of the obtained results given in Figure 1 and Table 2, it is concluded that the ground potential rise along the grid center conductor, the touch and step voltages along the center conductor and grid resistance reach their lowest value when the compression ratio for this grid reaches 0.493 and the grid number of meshes is 64. These results are in agreement with that obtained by Gouda [46].
Table 2: Summary of the relation between the GPR, step and touch potentials and grid resistance from one side and the compressed ratios from the other side, N=64.
| Compression Ratio (CR) | GPR (Volt) | Emesh (Volt) | Estep (Volt) | Ground Resistance (Ω) |
|---|---|---|---|---|
| CR=0 | 2480.5 | 601.49 | 245.7 | 0.4134 |
| CR=0.1 | 2295.3 | 559.26 | 238.45 | 0.3825 |
| CR=0.2 | 2178.6 | 486.98 | 213.08 | 0.3631 |
| CR=0.3 | 2116.6 | 417.96 | 188.28 | 0.3528 |
| CR=0.4 | 2106 | 313.57 | 145.4 | 0.351 |
| CR=0.493 | 2097.6 | 218.66 | 102.38 | 0.3496 |
| CR=0.6 | 2203.2 | 266.56 | 149.34 | 0.3672 |
| CR=0.7 | 2305.9 | 326.45 | 215.82 | 0.3843 |
| CR=0.8 | 2411.5 | 401.7 | 267.5 | 0.4019 |
| CR=0.9 | 2518.8 | 499.5 | 13.115 | 0.4198 |
| CR=1 | 2626.4 | 593.7 | 353.2 | 0.4377 |
To obtain the relation between the number of meshes and optimum compressed ratios, calculations are done when the short circuit current is 10 kA and the soil resistivity is 100 Ω.m. Figure 2 gives the relation between the ground grid potential rises (GPR) along the center of the square grounding grids for different values of compression ratios (CR).
Summary of the relations between the grid ground potential rise (GPR), step and touch potentials and grid resistance from one side and the compression ratios on the other side is given in Table 2.
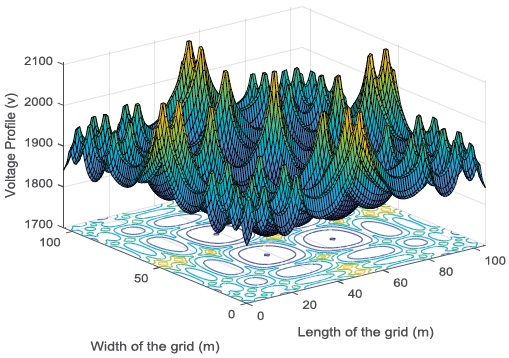
Unfortunately, it is found that the OCR value is not constant for all the grounding grids. Each grid with different number of meshes has its own OCR. Figure 2 illustrates the relationship between the grounding potential rise over the center conductor and the relation between OCR for the unequally spaced grid as a function of conductor compression ratio. Remarkable, these relationships usually have an obvious ‘’U’’ shape. It is noticed also from Figure 2 that increasing in the grid meshes number increases it’s OCR. As example OCR for 36 grid meshes is 0.31, it is 0.493 for N=64, 0.58 for N=100 and 0.65 for N=256. The voltage profile distribution samples in 3D for optimum compressed ratio value given in Figure 3. It is observed that at CR=0.493 the ground potential is more uniformly distributed.
Figure 3: The voltage profile along all grid conductors in case of unequally spaced grid having denser conductors at the edges of (A=105 × 105 m2, N=64) (Eq 12) in case of OCR=0.493.
Design of the Grounding Grid using Particle Swarm Optimization (PSO)
In this part of the paper, the step voltage, touch voltage, ground potential rise (GPR), and grounding resistance, based on ANSI/IEEE Std 80 and applying the particle swarm optimization (PSO) to obtain the optimal grounding grid design, which includes number of meshes, and is laying at known depth. Grid design has to consider factors of safety and minimum used copper. The design grid parameters of the grounding grid and used copper volume are estimated based on ANSI/IEEE Std 80 [2].
Total volume of the grounding grid conductors
Attention has to be considered for the copper grid volume. To have the optimal design of grounding grid with minimum cost, the objective volume function has to be optimized while satisfying the safety considerations and predetermined value of grounding resistance.
The copper volume of the grid conductors is evaluated as given in equation (13).
Where
d is grounding grid diameter of the conductor (m)
NLc is conductors number in the length direction
Nwc is conductors number in the width direction
dr is the ground rod diameter (m)
Safety criteria constraints and grounding resistance
The safety standard includes that the actual grid mesh and step potentials must be less than or even equal the values of the corresponding acceptable potentials which are borne by humans without being subjected to electric shocks.
The recommended limits of the grounding potential rise, GPR value is usually 5000V for the substations grounding grids [2].
The grounding resistance of the designed grid has to be equal or less than the target grid resistance.
For the most high-voltage and large substations, the grounding resistance is usually less than 0.5 Ω. In smaller substations, the acceptable value usually depends on the local conditions [2]. The conductors’ separation in x and y directions is proportional to the grounding grid dimensions as follows [2]. In case of unequally spaced grid, the space between the conductors depends on the designed compressed ratio.
The burial depth of the grid influences the ground potential rise and the grid resistance. According to standards, the grid burial depth is recommended to be between 0.25- 2.5 m.
Finally, a mathematical model is formulated in general constrained optimized problem.
f(x,v) is defined as the objective function, g(x,v) and h(x,v) are defined as the set of equality and inequality constraints, respectively, x is known as state variables and v is the vector of variables. The control variables depend on the designer vision.
Applications of the PSO algorithm in grounding grid design
The field data that are given in Table 3 is used for the designing of grounding grid by using PSO algorithm. The control variables considered in the design using PSO algorithm are the spacing between the grid adjacent conductors (continuous variable), the grid burial depth (continuous variable), rods number (integer number and continuous variable), and the grounding conductor crosssectional area (discrete variable). The PSO algorithm and the grounding grid optimization flowchart is given in [36].
Table 3: The field data of the grounding system.
| Grid parameter | Field data |
|---|---|
| A (Grid area, m2) | 105 × 105 m2 |
| ρ (Soil resistivity, Ωm) | 100 Ωm |
| If ( Fault current, A) | 10000 Amp |
| Df ( Decrement factor) | 1 |
| Sf (Current division factor) | 0.6 |
| tf (Duration of fault current) | 1 sec |
| ts ( Duration of shock) | 1 sec |
| ρs (Crushed Rock Resistivity) | 2500 Ω.m |
| hs (Thickness of Crushed Rock) | 0.102 m |
| Diameter of the conductors | 0.01 m |
| Etouch-tolerable | 572.72 v |
| Estep-tolerable | 1819.9 v |
The obtained designed parameters are given in Table 4 and it is compared with the parameters of grounding grid equally spaced between each conductor that is designed by using IEEE Std 80-2000. It is noticed that the design of the grounding grid using PSO algorithm gives saving in copper volume and mass of the grounding grid by about 24.9% and decreases the step potential by 12.3%, but unfortunately, an increase in GPR and the mesh voltage by 5.5% and 4.9% respectively is noticed. It should be noted that nevertheless these values give a safe design for the grounding grid and meets the requirements of the design (Table 5).
Table 4: Grounding grid parameters using IEEE std 80-2000 and PSO without using rods.
| Ground grid design without using rods | Using IEEE Std 80-2000 | Using PSO |
|---|---|---|
| h (laying depth, m) | 1 | 0.9 |
| D (Spacing between each conductor and the other, m) | 15 | 21 |
| NLc (Number of conductors in each side) | 8 | 6 |
| Volume (m3) | 0.1319 | 0.0990 |
| Mass (kg) | 1179.18 | 885.06 |
| GPR (v) | 2553.9 | 2695.2 |
| Estep (v) | 303.35 | 266.01 |
| Emesh (v) | 538.92 | 565.51 |
| Ground Resistance (Ω) | 0.4257 | 0.4492 |
Table 5: Grounding grid parameters using IEEE std 80-2000 and PSO with using rods, equal space between conductors.
| Ground grid design with rods | Using IEEE Std 80-2000 | Using PSO |
|---|---|---|
| h (laying depth, m) | 1.5 | 1.1 |
| D (Spacing between each conductor and the other, m) | 26.25 | 35 |
| NLc(Number of conductors in each side) | 5 | 4 |
| Nr (Number of rods) | 17 | 16 |
| Lr (Rod length, m) | 3 | 3 |
| Dr (Rod diameter, m) | 0.03 | 0.03 |
| Volume (m3) | 0.1185 | 0.0999 |
| Mass (kg) | 1059.39 | 893.106 |
| GPR (v) | 2566 | 2755.5 |
| Estep (v) | 215.53 | 185.03 |
| Emesh (v) | 476.87 | 559.11 |
| Ground Resistance (Ω) | 0.4277 | 0.4593 |
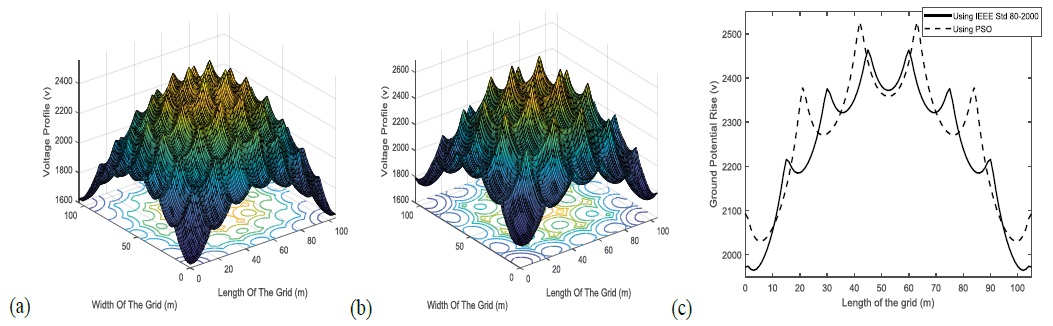
The voltage profile of the grounding grid design using IEEE Std 80-2000 and using PSO in the 3-D and also the GPR in 2-D are given in Figure 4.
Figure 4: Voltage profile of the ground system design, (a) using IEEE Std 80-2000 (b) using PSO in 3-D and (c) GPR of grounding grid using IEEE Std 80-2000 and PSO in 2-D.
Design of the Grounding Grid using Hybridization Between CR and PSO Algorithm Uniform soil
Hybridization of the CR method and PSO algorithm is done to obtain the most economical and safe grounding grid. It can be considered as an evolutionary technique for the unequally spaced grounding grid design. In this technique, the compressed ratio CR is taken as one of the variables that are optimized by PSO. One advantage of the suggested method is to obtain unequally space, economical and safe grounding grid design.
The control variables considered are the spacing between conductors, the required copper volume and the number of conductors in each side. It is found that the optimized value of CR is 0.23 in the case under study (A square grounding grids of 105 × 105 m2 area, buried in 100 ohm m uniform soil resistivity and the current emanating from this grid into the soil is 10 kA). Figure 4 (a) shows the voltage profile in 3-D of the grounding grid designed by using IEEE Std 80- 2000. Figure 4 (b) gives the voltage profile by using PSO in 3-D. GPR of grounding grid by using IEEE Std 80-2000 and PSO in 2-D is given in Figure 4(c). Table 6 gives the design parameters of the grounding grid system by using OCR and PSO, the grid conductors are unequally spaced.
Table 6: Design of the grounding grid using OCR and PSO, the grid conductors are unequally spaced.
| Ground grid design | Using CR | Using OCR | New technique |
|---|---|---|---|
| CR | 0.9 | 0.119 | 0.23 |
| h | 1.5 | 1.5 | 1.5 |
| D (Conductor spacing m), NLc | [17.5-35-35-17.5], 5 | [17.5-35- 35-17.5], 5 | [26.25- 52.5-26.25], 4 |
| Volume (m3) | 0.0825 | 0.0825 | 0.0660 |
| Mass (kg) | 737.55 | 737.55 | 590 |
| GPR (v) | 2656.6 | 2252.4 | 2327.2 |
| Estep (v) | 204.55 | 109.08 | 128.14 |
| Emesh (v) | 472.56 | 295.43 | 429.15 |
| Resistance (Ω) | 0.4428 | 0.3754 | 0.3879 |
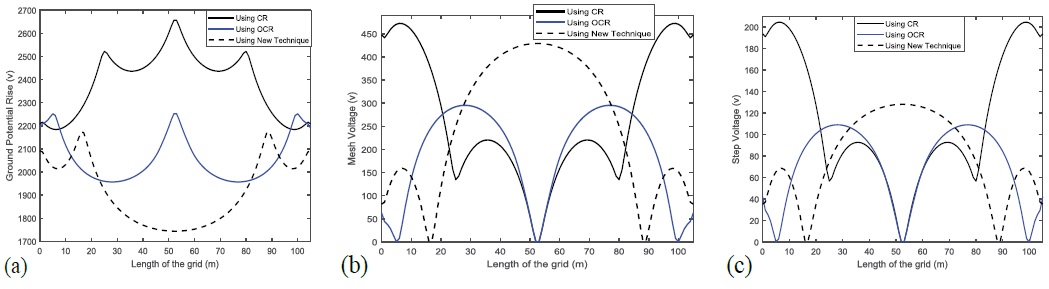
The comparison is done between grid designed by using the new technique, using OCR method and also by using compressed ratio equals 0.9 as given in Table 6. Figure 5 (a) shows the ground potential rise of the three grids, Figure 5 (b) shows the mesh voltage and Figure 5 (c) gives the step voltage of the designed grids. Using the new technique in the grounding grid design indicates that 4 conductors only in each side of the grid gave economical and safe grounding grid. From Table 6 it is noticed that 19.27% saving in copper volume of the grounding grid is done by using the new technique and slight increase is observed in the grid resistance, ground potential rise and mesh voltage comparing with using OCR and CR=0.9 methods in the design of the grounding grid, with acceptable safe design.
Figure 5: Voltages of grounding grid design, (a) GPR, (b) Mesh voltage and (c) Step voltage of the designed grids given in Table 6.
Non-uniform soil
The apparent soil resistivity of two-layer soil can be evaluated using the following formulas that are developed by Sunde [47]:
The apparent soil resistivity of three layers’ soil can be evaluated using the following method:
Where
ρao: Apparent soil resistivity between first and second
layer
ρ1: First layer soil resistivity
ρ2: Second layer soil resistivity
S: the spacing between probe electrodes of measuring
soil resistivity.
d1: First layer soil thickness
δ : Scaling factor
The apparent soil resistivity of three layers’ soil can be evaluated using the following method:
The apparent soil resistivity of three soil layers is obtained by evaluating initial apparent soil resistivity between the first and second layer that is represented by (ρao) by using ED. Sunde equation (20) [47]. Then considering the initial apparent soil resistivity which evaluated between t first and second layers (ρao) as a first layer and then, considering the third layer resistivity as a second one. Thus the apparent soil resistivity of the three layers can be calculated as follows:
Where
ρao: Apparent soil resistivity between first and second
layer
ρa: The apparent soil resistivity, ρ3 Third layer soil
resistivity
d2: Second layer soil thickness, d1 First layer soil thickness
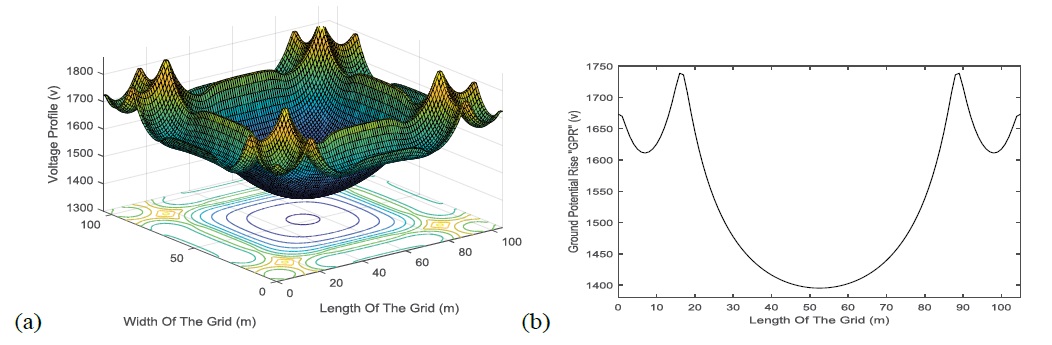
For the design of grounding grid using hybridization between CR method and PSO Algorithm (New technique) in case of two or three layers soil, first of all the apparent soil resistivity has to be calculated by using the above explained method or measured by using four electrodes method (Winner method). Then the peak value of the calculated or measured apparent soil resistivity with respect the space between the electrodes will be used in the grounding system design. The apparent soil resistivity in the above example is taken 80 Ωm. The designed grid parameters using the new technique are given in Table 7. It is found that the optimized value of CR is 0.23 in the case under study, square grounding grids of 105 × 105 m2 area, buried in the first layer of the three layers and 80 Ω.m apparent soil resistivity of the three layers. The current emanating from this grid into the soil is 10 kA. Figure 6 (a) shows the voltage profile in 3-D of the grounding grid designed by the suggested technique and Figure 6 (b) shows the ground potential rise.
Table 7: Grounding grid parameters of three layers by using the suggested technique.
| Ground grid design | Using suggested technique |
|---|---|
| Soil resistivity | 80 Ω.m |
| CR | 0.23 |
| H | 1.5 |
| D | [26.25 52.5 26.25] , 4 |
| NLc | 4 |
| Volume (m3) | 0.0660 |
| Mass (kg) | 590 |
| GPR (v) | 1861.7 |
| Estep (v) | 102.51 |
| Emesh (v) | 343.32 |
| Ground Resistance (Ω) | 0.3103 |
Figure 6: Voltages of grounding grid design using the new technique of three layers example (apparent soil resistivity is 80 Ω.m) (a) Voltage profile (b) Ground potential rise.
Conclusion
In this paper, the design methods of grounding grid using optimum compression ratio method and particle swarm optimization technique are presented. It has been found that each grid has its own OCR depending on the grid meshes number. Hybridization of compression ratio and PSO techniques is suggested. This approach is purposed to control the grounding copper volume of the grounding grid with the aid of controlling the grid conductors’ length under the safety limitations. The proposed technique offers almost 20% of copper savings while respecting all design requirements and safety measures. Hence it is obvious that the suggested method is quite satisfactory for the design of grounding system in uniform as well as multi-layered soils and meets IEEE safety criteria. Hence this technique proves to be an effective method and copper savings for preliminary design at least of the optimum grounding grid, rather than using the experience rules.
There are no references